احتمال تقاطع الأحداث

تشرح هذه المقالة كيفية حساب احتمال تقاطع الأحداث. لذلك سوف تكتشف ما هي صيغة احتمال تقاطع الأحداث، بالإضافة إلى التمارين التي يتم حلها خطوة بخطوة.

ما هو تقاطع الأحداث؟

في نظرية الاحتمالات، تقاطع الأحداث هو عملية من الأحداث التي تتكون نتيجتها من أحداث أولية مشتركة بين جميع أحداث العملية. أي أن تقاطع الحدثين A وB يتكون من جميع الأحداث التي تنتمي إلى A وB في نفس الوقت.

يتم التعبير عن تقاطع حدثين بالرمز ⋂. ومن ثم، فإن تقاطع الحدثين A وB يُكتب A⋂B.

على سبيل المثال، في التجربة العشوائية لرمي حجر النرد، إذا كان أحد الأحداث هو ظهور رقم زوجي A={2, 4, 6} وحدث آخر هو ظهور رقم أكبر من ثلاثة B={4, 5, 6 }، فإن تقاطع الحدثين هو A⋂B={4, 6}.

صيغة لاحتمال تقاطع الأحداث

احتمال تقاطع حدثين يساوي احتمال وقوع حدث واحد مضروبًا في الاحتمال الشرطي لوقوع الحدث الآخر بمعلومية الحدث الأول.

ولذلك، فإن صيغة احتمال تقاطع حدثين هي P(A⋂B)=P(A) P(B|A)=P(B) P(A|B).

ذهب:

• 

  و

  

  وهذان حدثان معتمدان.

• 

  هو احتمال تقاطع الحدث A مع الحدث B.

• 

  هو احتمال وقوع الحدث A.

• 

  هو الاحتمال المشروط لحدوث الحدث B في ضوء الحدث A.

• 

  هو احتمال وقوع الحدث B.

• 

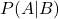
  هو الاحتمال المشروط لوقوع الحدث A في ضوء الحدث B.

ومع ذلك، إذا كان الحدثان مستقلين، فهذا يعني أن احتمال وقوع حدث واحد لا يعتمد على ما إذا كان الحدث الآخر قد وقع أم لا. ولذلك فإن صيغة احتمال تقاطع الحدثين المستقلين هي كما يلي:

ذهب:

• 

  و

  

  وهذان حدثان مستقلان.

• 

  هو احتمال تقاطع الحدث A والحدث B.

• 

  هو احتمال وقوع الحدث A.

• 

  هو احتمال وقوع الحدث B.

أمثلة من العالم الحقيقي لاحتمال تقاطع الحدث

بعد ذلك، نترك لك مثالين تم حلهما خطوة بخطوة حتى تتمكن من رؤية كيفية حساب احتمال تقاطع حدثين. سنرى أولا مثالا على تقاطع حدثين مستقلين ثم حدثين مستقلين، حتى تتمكن من رؤية الحالتين.

احتمال تقاطع حدثين مستقلين

• يتم إجراء السحب ثلاث مرات متتالية. أوجد احتمال الحصول على صورة في الرميات الثلاث.

في هذه الحالة، تكون الأحداث التي نريد حساب الاحتمال المشترك لها مستقلة، حيث أن نتيجة التعادل لا تعتمد على النتيجة التي تم الحصول عليها في السحب السابق. لذلك، لتحديد احتمال الحصول على ثلاثة رؤوس متتالية، يجب علينا استخدام صيغة احتمال التقاطع للأحداث المستقلة:

عند إجراء القرعة، هناك نتيجتان محتملتان فقط، يمكننا الحصول على صورة أو كتابة. وبالتالي، فإن احتمال الحصول على صورة أو كتابة عند رمي قطعة نقود هو:

لذا، لإيجاد احتمال الحصول على صورة عند رمي العملات الثلاث، نحتاج إلى ضرب احتمال الحصول على صورة في ثلاثة:

باختصار، احتمال الحصول على صورة ثلاث مرات متتالية هو 12.5%.

احتمال تقاطع حدثين تابعين

• في صندوق فارغ، نضع 8 كرات زرقاء، 4 كرات برتقالية و2 كرات خضراء. إذا سحبنا كرة واحدة أولًا ثم كرة أخرى دون إعادة الكرة الأولى المسحوبة إلى الصندوق، فما احتمال أن تكون الكرة الأولى زرقاء والكرة الثانية برتقالية؟

وفي هذه الحالة تعتمد الأحداث، لأن احتمال التقاط كرة برتقالية في السحب الثاني يعتمد على لون الكرة المسحوبة في السحب الأول. لذلك، لحساب الاحتمال الذي تطلبه منا المشكلة، يجب علينا استخدام صيغة احتمال التقاطع للأحداث التابعة:

من السهل تحديد احتمالية الحصول على كرة زرقاء في السحب الأول، ما عليك سوى قسمة عدد الكرات الزرقاء على إجمالي عدد الكرات:

من ناحية أخرى، فإن احتمال سحب كرة برتقالية بعد أخذ كرة زرقاء يتم حسابه بشكل مختلف لأن عدد الكرات البرتقالية مختلف، وبالإضافة إلى ذلك، هناك الآن كرة أقل داخل الصندوق:

وبالتالي، يتم حساب احتمال سحب كرة زرقاء أولاً ثم كرة برتقالية عن طريق ضرب الاحتمالين الموجودين أعلاه:

خصائص تقاطع الحدث

في نظرية الاحتمالات، تقاطع الأحداث له الخصائص التالية:

• الخاصية التبادلية: ترتيب أحداث التقاطع لا يغير نتيجة العملية.

• الخاصية الترابطية: يمكن حساب تقاطع ثلاثة أحداث بأي ترتيب، لأن النتيجة واحدة.

• خاصية التوزيع: تقاطع الأحداث يحقق خاصية التوزيع عند اتحاد الأحداث.