كيفية اختبار الحالة الطبيعية في لغة بايثون (4 طرق)

تفترض العديد من الاختبارات الإحصائية أن مجموعات البيانات يتم توزيعها بشكل طبيعي.

هناك أربع طرق شائعة للتحقق من هذه الفرضية في بايثون:

1. (الطريقة المرئية) قم بإنشاء رسم بياني.

• إذا كان الرسم البياني على شكل “جرس” تقريبًا، فمن المفترض أن يتم توزيع البيانات بشكل طبيعي.

2. (الطريقة المرئية) قم بإنشاء مخطط QQ.

• إذا كانت النقاط الموجودة على المخطط تقع تقريبًا على طول خط قطري مستقيم، فمن المفترض أن يتم توزيع البيانات بشكل طبيعي.

3. (اختبار إحصائي رسمي) قم بإجراء اختبار شابيرو ويلك.

• إذا كانت القيمة p للاختبار أكبر من α = 0.05، فمن المفترض أن يتم توزيع البيانات بشكل طبيعي.

4. (اختبار إحصائي رسمي) إجراء اختبار كولموجوروف-سميرنوف.

• إذا كانت القيمة p للاختبار أكبر من α = 0.05، فمن المفترض أن يتم توزيع البيانات بشكل طبيعي.

توضح الأمثلة التالية كيفية استخدام كل من هذه الطرق عمليًا.

الطريقة الأولى: إنشاء رسم بياني

يوضح التعليمة البرمجية التالية كيفية إنشاء رسم بياني لمجموعة بيانات تتبع توزيع السجل الطبيعي :

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

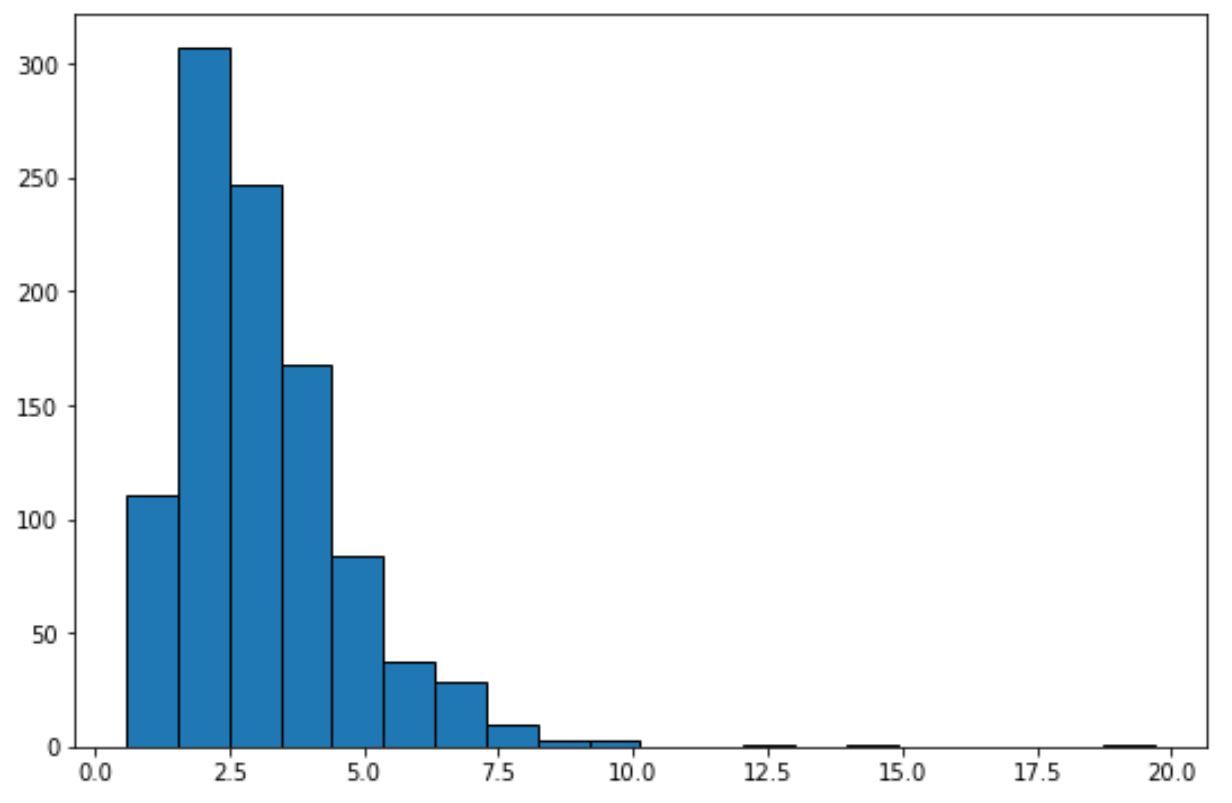
بمجرد النظر إلى هذا الرسم البياني، يمكننا أن نقول أن مجموعة البيانات لا تظهر “شكل الجرس” ولا يتم توزيعها بشكل طبيعي.

الطريقة الثانية: إنشاء مخطط QQ

يوضح التعليمة البرمجية التالية كيفية إنشاء مخطط QQ لمجموعة بيانات تتبع توزيع السجل الطبيعي:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

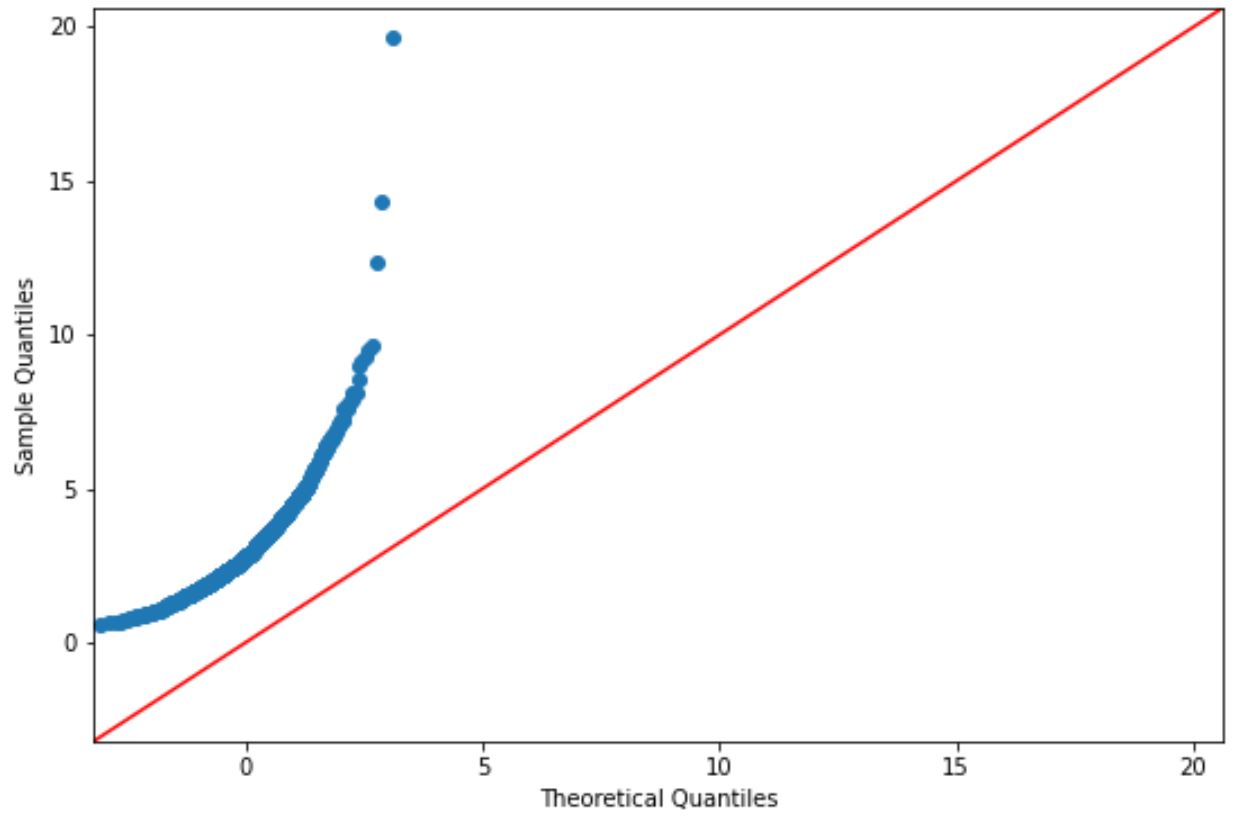
إذا كانت نقاط الرسم تقع تقريبًا على طول خط قطري مستقيم، فإننا نفترض عمومًا أن مجموعة البيانات يتم توزيعها بشكل طبيعي.

ومع ذلك، فمن الواضح أن النقاط الموجودة على هذا الرسم البياني لا تتوافق مع الخط الأحمر، لذلك لا يمكننا افتراض أن مجموعة البيانات هذه يتم توزيعها بشكل طبيعي.

يجب أن يكون هذا منطقيًا نظرًا لأننا أنشأنا البيانات باستخدام دالة توزيع السجل الطبيعي.

الطريقة الثالثة: إجراء اختبار شابيرو ويلك

يوضح التعليمة البرمجية التالية كيفية إجراء Shapiro-Wilk لمجموعة بيانات تتبع توزيع السجل الطبيعي:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

من النتيجة، يمكننا أن نرى أن إحصائيات الاختبار هي 0.857 والقيمة p المقابلة هي 3.88e-29 (قريبة جدًا من الصفر).

وبما أن القيمة p أقل من 0.05، فإننا نرفض الفرضية الصفرية لاختبار شابيرو ويلك.

وهذا يعني أن لدينا ما يكفي من الأدلة لنقول أن بيانات العينة لا تأتي من التوزيع الطبيعي.

الطريقة الرابعة: إجراء اختبار كولموجوروف-سميرنوف

يوضح التعليمة البرمجية التالية كيفية إجراء اختبار Kolmogorov-Smirnov لمجموعة بيانات تتبع توزيع السجل الطبيعي:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

من النتيجة يمكننا أن نرى أن إحصائيات الاختبار هي 0.841 والقيمة p المقابلة هي 0.0 .

وبما أن القيمة p أقل من 0.05، فإننا نرفض الفرضية الصفرية لاختبار كولموجوروف-سميرنوف.

وهذا يعني أن لدينا ما يكفي من الأدلة لنقول أن بيانات العينة لا تأتي من التوزيع الطبيعي.

كيفية التعامل مع البيانات غير العادية

إذا لم يتم توزيع مجموعة بيانات معينة بشكل طبيعي، فيمكننا غالبًا إجراء أحد التحويلات التالية لجعلها موزعة بشكل طبيعي أكثر:

1. تحويل السجل: تحويل قيم x إلى log(x) .

2. تحويل الجذر التربيعي: قم بتحويل قيم x إلى √x .

3. تحويل الجذر التكعيبي: تحويل قيم x إلى x ^1/3 .

ومن خلال إجراء هذه التحويلات، تصبح مجموعة البيانات موزعة بشكل طبيعي أكثر.

اقرأ هذا البرنامج التعليمي لمعرفة كيفية إجراء هذه التحولات في بايثون.