ما هو اختبار الغذاء؟ (شرح ومثال)
اختبار تشاو هو اختبار إحصائي تم تطويره من قبل الاقتصادي جريجوري تشاو ويستخدم لاختبار ما إذا كانت معاملات نموذجي الانحدار المختلفين في مجموعات بيانات مختلفة متساوية.
يُستخدم اختبار تشاو عادةً في مجال الاقتصاد القياسي مع بيانات السلاسل الزمنية لتحديد ما إذا كان هناك انقطاع هيكلي في البيانات في وقت معين.
على سبيل المثال، خذ بعين الاعتبار المخطط المبعثر التالي:
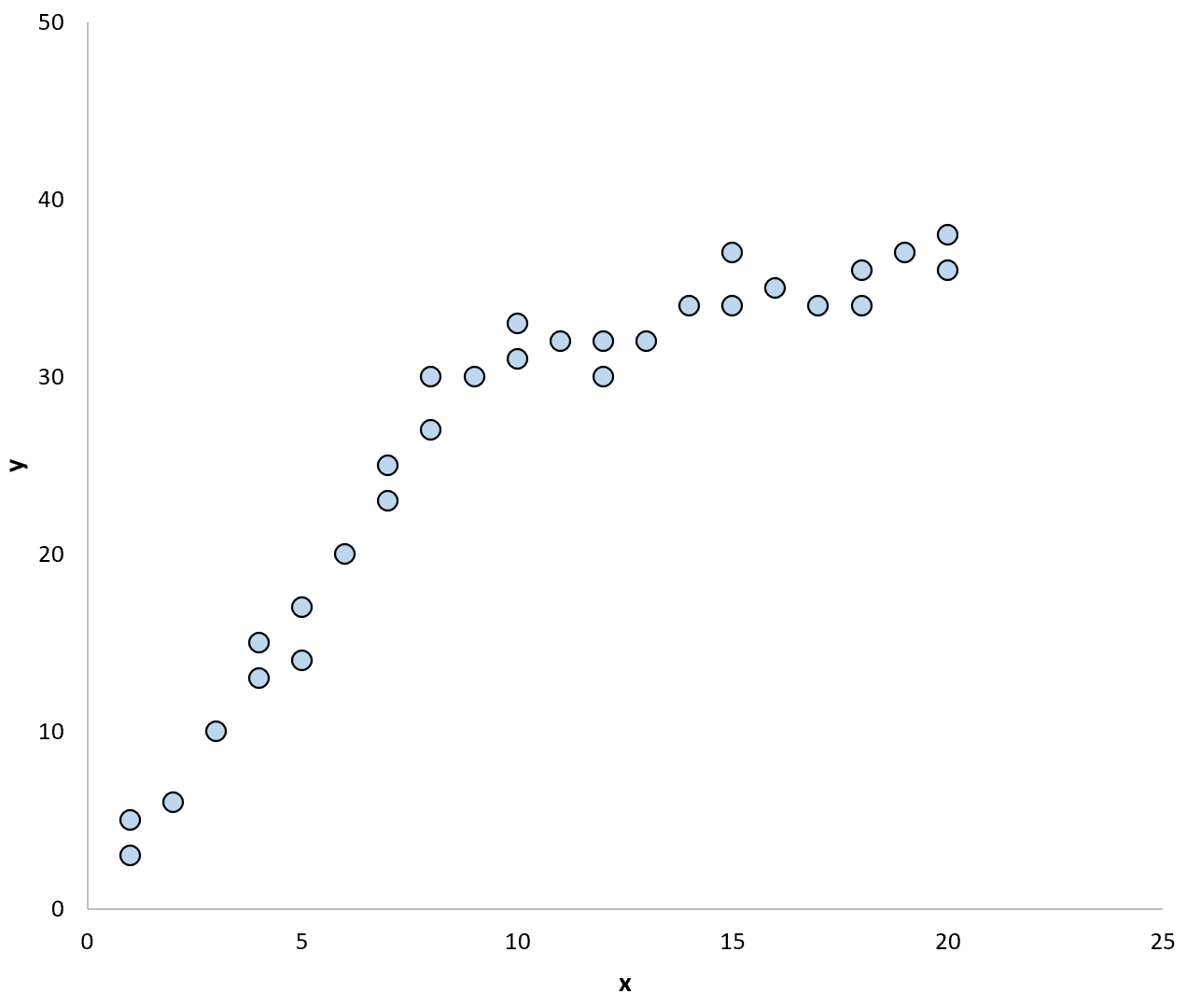
إذا استخدمنا خط الانحدار لتلخيص النموذج في البيانات، فقد يبدو كما يلي:
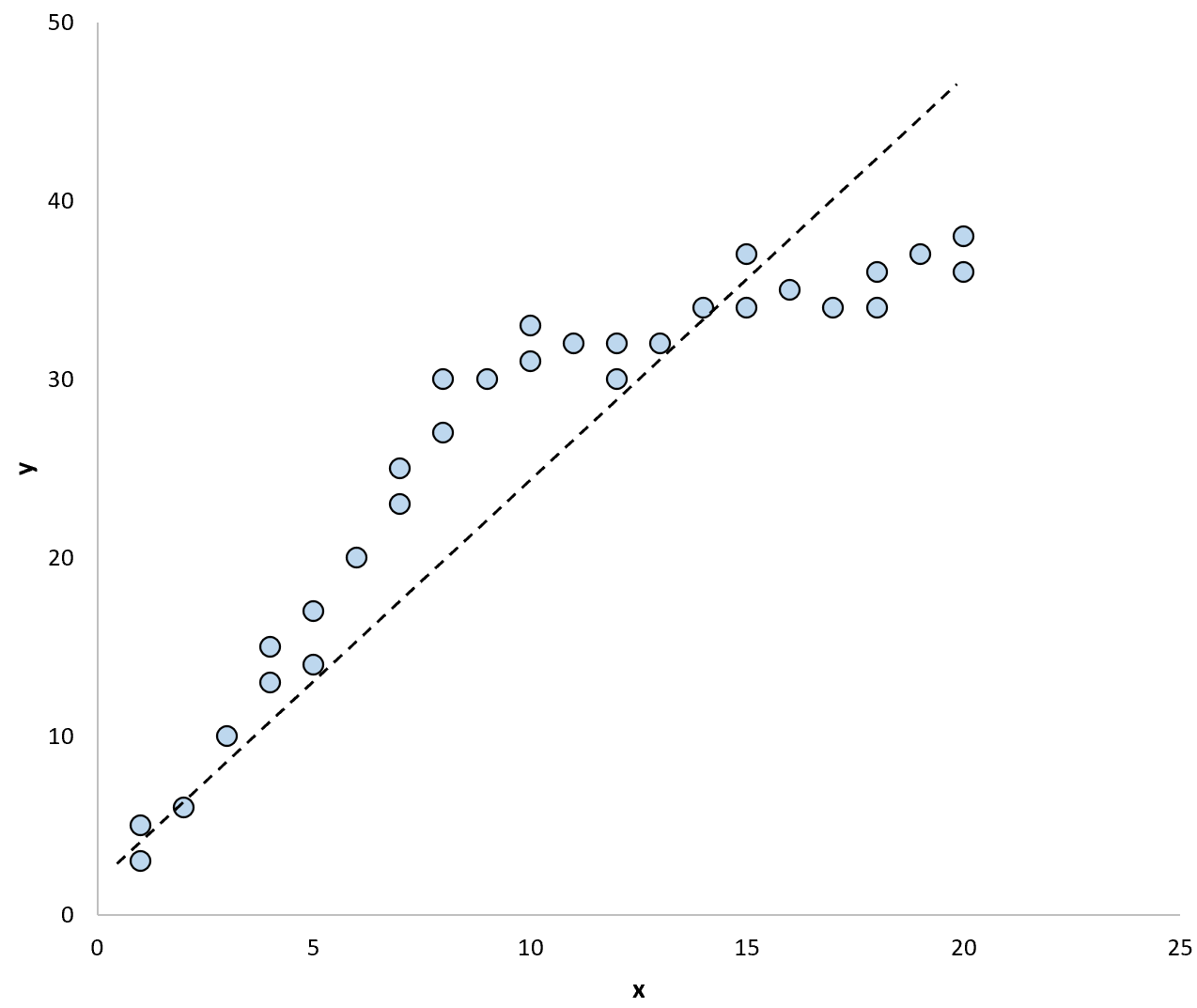
وإذا استخدمنا خطي انحدار منفصلين لتلخيص النموذج في البيانات، فقد يبدو كما يلي:
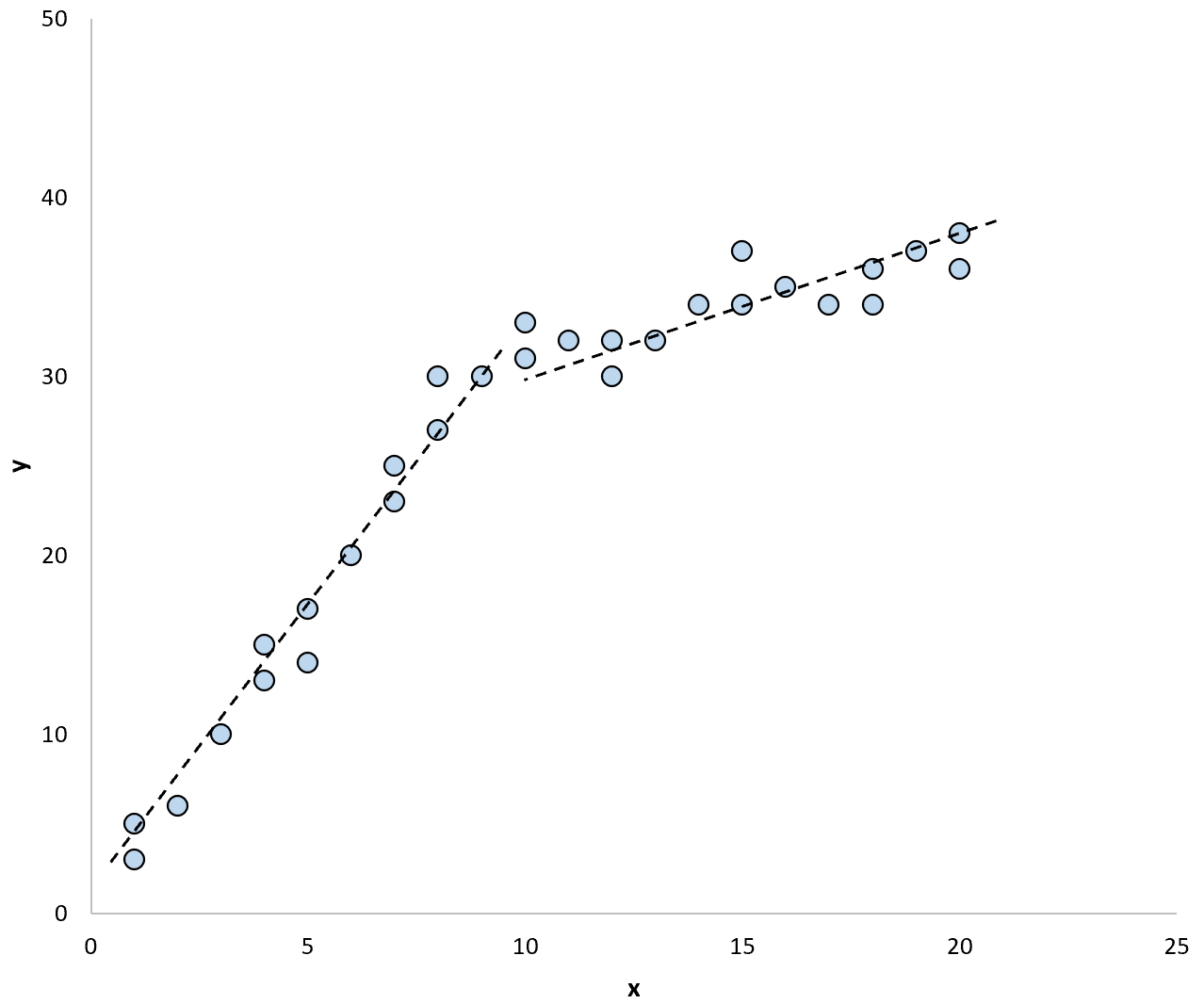
يتيح لنا اختبار تشاو اختبار ما إذا كانت معاملات الانحدار لكل خط انحدار متساوية أم لا.
إذا حدد الاختبار أن المعاملات غير متساوية بين خطوط الانحدار، فهذا يعني أن هناك دليلا كبيرا على وجود انقطاع هيكلي في البيانات. وبعبارة أخرى، فإن اتجاه البيانات يختلف تمامًا قبل وبعد نقطة الانهيار الهيكلي هذه.
متى يتم استخدام اختبار تشاو
توضح الأمثلة التالية المواقف التي قد ترغب في إجراء اختبار تشاو فيها:
1. تحديد ما إذا كانت أسعار الأسهم تتحرك بمعدلات مختلفة قبل الانتخابات وبعدها.
2. تحديد ما إذا كانت أسعار المنازل تتغير قبل وبعد تغيير سعر الفائدة.
3. تحديد ما إذا كان متوسط ربح المؤسسات العامة مختلفًا قبل وبعد اعتماد قانون الضرائب الجديد.
في كل حالة، يمكننا استخدام اختبار تشاو لتحديد ما إذا كانت هناك نقطة انقطاع هيكلية في البيانات في أي وقت معين.
خطوات إجراء اختبار تشاو
يمكننا استخدام الخطوات التالية لإجراء اختبار تشاو.
الخطوة الأولى: تحديد الفرضيات الصفرية والبديلة.
لنفترض أننا نلائم نموذج الانحدار التالي مع مجموعة البيانات بأكملها:
- y t = أ + بx 1t + cx t2 + ε
بعد ذلك، لنفترض أننا قسمنا بياناتنا إلى مجموعتين بناءً على نقطة توقف هيكلية وتناسب نماذج الانحدار التالية مع كل مجموعة:
- ذ ر = أ 1 + ب 1 × 1 طن + ج 1 × t2 + ε
- ذ ر = أ 2 + ب 2 × 1 طن + ج 2 × t2 + ε
سوف نستخدم الفرضيات الصفرية والبديلة التالية لاختبار تشاو:
- خالية (ح 0 ): أ 1 = أ 2 ، ب 1 = ب 2 و ج 1 = ج 2
- البديل (HA A ): واحد على الأقل من المقارنات في Null غير متساوٍ.
إذا رفضنا فرضية العدم، فلدينا أدلة كافية لنقول أن هناك نقطة توقف هيكلية في البيانات وأن خطي الانحدار يمكن أن يتناسبا مع البيانات بشكل أفضل من خط واحد.
إذا فشلنا في رفض فرضية العدم، فليس لدينا ما يكفي من الأدلة لنقول أن هناك نقطة توقف هيكلية في البيانات. في هذه الحالة، نقول أنه يمكن “تجميع” خطوط الانحدار في خط انحدار واحد يمثل نمط البيانات بشكل جيد بما فيه الكفاية.
الخطوة 2: حساب إحصائية الاختبار.
فإذا عرفنا المصطلحات التالية:
- S T : مجموع مربعات بقايا البيانات الإجمالية
- S 1 , S 2 : مجموع مربعات بقايا كل مجموعة
- ن 1 , ن 2 : عدد المشاهدات في كل مجموعة
- ك: عدد المعلمات
يمكننا بعد ذلك القول أن إحصائيات اختبار تشاو هي:
إحصائية اختبار تشاو = [(S T – (S 1 +S 2 ))/ك] / [(S 1 +S 2 )/ (N 1 +N 2 -2k)]
تتبع إحصائية الاختبار توزيع F بدرجات حرية k وN 1 +N 2 -2k.
الخطوة 3: رفض أو عدم رفض الفرضية الصفرية.
إذا كانت القيمة p المرتبطة بإحصائيات الاختبار هذه أقل من مستوى معين من الأهمية ، فيمكننا رفض فرضية العدم ونستنتج أن هناك نقطة انقطاع هيكلية في البيانات.
لحسن الحظ، معظم البرامج الإحصائية قادرة على إجراء اختبار تشاو، لذلك ربما لن تضطر أبدًا إلى إجراء الاختبار يدويًا.
مثال على إجراء اختبار تشاو
ارجع إلى هذا البرنامج التعليمي للاطلاع على مثال خطوة بخطوة حول كيفية إجراء اختبار Chow لمجموعة بيانات معينة في R.
ملاحظات اختبار تشاو
فيما يلي بعض الملاحظات التي يجب وضعها في الاعتبار حول اختبار تشاو:
1. يفترض الاختبار أن بقايا نماذج الانحدار موزعة بشكل مستقل ومتماثل عنالتوزيع الطبيعي مع تباين غير معروف.
2. يجب استخدام اختبار تشاو فقط عندما يحدث الكسر الهيكلي الذي ترغب في اختباره في وقت معروف . وبعبارة أخرى، لا ينبغي استخدام الاختبار مرارا وتكرارا لتحديد ما إذا كان يمكن اعتبار لحظة معينة انقطاعا هيكليا.
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر