اختبار t ذو عينتين: التعريف والصيغة والمثال
يتم استخدام اختبار t المكون من عينتين لتحديد ما إذا كانت متوسطات مجتمعين متساويتين أم لا.
يشرح هذا البرنامج التعليمي ما يلي:
- الدافع لإجراء اختبار t المكون من عينتين.
- صيغة إجراء اختبار t المكون من عينتين.
- الافتراضات التي يجب توافرها لإجراء اختبار (ت) ذو العينتين.
- مثال على كيفية إجراء اختبار t المكون من عينتين.
اختبار t من عينتين: الدافع
لنفترض أننا نريد أن نعرف ما إذا كان متوسط وزن نوعين مختلفين من السلاحف متساويًا أم لا. نظرًا لوجود الآلاف من السلاحف في كل مجموعة، سيكون الأمر مكلفًا للغاية ويستهلك الكثير من الوقت للتجول ووزن كل سلحفاة على حدة.
بدلًا من ذلك، يمكننا أخذ عينة عشوائية بسيطة مكونة من 15 سلحفاة من كل مجموعة واستخدام متوسط وزن كل عينة لتحديد ما إذا كان متوسط الوزن متساويًا بين المجموعتين:
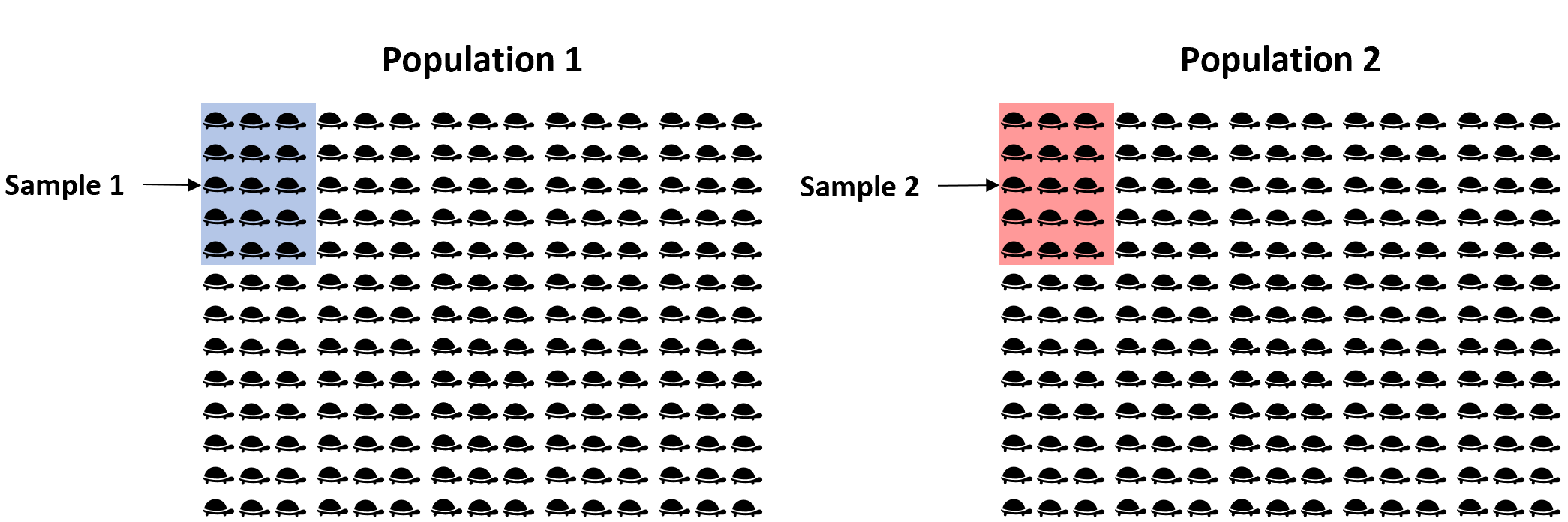
ومع ذلك، فمن المؤكد تقريبًا أن متوسط الوزن بين العينتين سيكون مختلفًا قليلاً على الأقل. والسؤال هو ما إذا كان هذا الاختلاف ذو دلالة إحصائية . ولحسن الحظ، فإن اختبار t المكون من عينتين يسمح لنا بالإجابة على هذا السؤال.
اختبار t لعينتين: الصيغة
يستخدم اختبار t المكون من عينتين دائمًا فرضية العدم التالية:
- H 0 : μ 1 = μ 2 (متوسطا السكان متساويان)
يمكن أن تكون الفرضية البديلة ثنائية أو يسارية أو يمينية:
- H 1 (ثنائي الذيل): μ 1 ≠ μ 2 (متوسط المجموعتين غير متساويين)
- H 1 (يسار): μ 1 < μ 2 (متوسط السكان 1 أقل من متوسط السكان 2)
- H 1 (يمين): μ 1 > μ 2 (متوسط السكان 1 أكبر من متوسط السكان 2)
نستخدم الصيغة التالية لحساب إحصائية اختبار t:
إحصائية الاختبار: ( x 1 – x 2 ) / ق ص (√ 1/ن 1 + 1/ن 2 )
حيث x 1 و x 2 هما متوسطا العينة، وn 1 وn 2 هما حجما العينة، وحيث يتم حساب s p على النحو التالي:
ث ع = √ (ن 1 -1)ث 1 2 + (ن 2 -1)ث 2 2 / (ن 1 +ن 2 -2)
حيث s 1 2 و s 2 2 هما تباينات العينة.
إذا كانت القيمة p التي تتوافق مع إحصائية اختبار t مع درجات الحرية (n 1 + n 2 -1) أقل من مستوى الأهمية الذي اخترته (الاختيارات الشائعة هي 0.10، 0.05، و0، 01)، فأنت يمكن رفض فرضية العدم. .
اختبار t لعينتين: الفرضيات
لكي تكون نتائج اختبار t المكون من عينتين صحيحة، يجب استيفاء الافتراضات التالية:
- يجب أن تكون ملاحظات إحدى العينات مستقلة عن ملاحظات العينة الأخرى.
- يجب أن يتم توزيع البيانات بشكل طبيعي تقريبًا.
- يجب أن يكون للعينتين نفس التباين تقريبًا. إذا لم يتم استيفاء هذا الافتراض، فيجب عليك إجراء اختبار Welch’s t بدلاً من ذلك.
- تم الحصول على البيانات من كلا العينتين باستخدام طريقة أخذ العينات العشوائية .
اختبار t لعينتين : مثال
لنفترض أننا نريد أن نعرف ما إذا كان متوسط وزن نوعين مختلفين من السلاحف متساويًا أم لا. ولاختبار ذلك، سنقوم بإجراء اختبار t مكون من عينتين عند مستوى الأهمية α = 0.05 باستخدام الخطوات التالية:
الخطوة 1: جمع بيانات العينة.
لنفترض أننا قمنا بجمع عينة عشوائية من السلاحف من كل مجموعة بالمعلومات التالية:
العينة 1:
- حجم العينة ن 1 = 40
- متوسط وزن العينة × 1 = 300
- نموذج الانحراف المعياري ق 1 = 18.5
العينة 2:
- حجم العينة ن 2 = 38
- متوسط وزن العينة × 2 = 305
- عينة الانحراف المعياري ق 2 = 16.7
الخطوة الثانية: تحديد الافتراضات.
سنقوم بإجراء اختبار t المكون من عينتين مع الافتراضات التالية:
- H 0 : μ 1 = μ 2 (متوسطا السكان متساويان)
- H 1 : μ 1 ≠ μ 2 (وسطا السكان غير متساويين)
الخطوة 3: حساب إحصائية اختبار t .
أولا، سوف نقوم بحساب الانحراف المعياري المجمع s p :
ث ع = √ (ن 1 -1)ث 1 2 + (ن 2 -1)ث 2 2 / (ن 1 +ن 2 -2) = √ ( 40-1)18.5 2 + (38-1) 16.7 2 / (40+38-2) = 17.647
بعد ذلك، سوف نقوم بحساب إحصائية اختبار t :
t = ( x 1 – x 2 ) / ث p (√ 1/n 1 + 1/n 2 ) = (300-305) / 17.647(√ 1/40 + 1/38 ) = -1.2508
الخطوة 4: احسب القيمة الاحتمالية لإحصائيات اختبار t .
وفقًا لـ T Score to P Value Calculator ، فإن القيمة p المرتبطة بـ t = -1.2508 ودرجات الحرية = n 1 + n 2 -2 = 40+38-2 = 76 هي 0.21484 .
الخطوة 5: استخلاص النتيجة.
وبما أن هذه القيمة p ليست أقل من مستوى الأهمية لدينا α = 0.05، فإننا نفشل في رفض فرضية العدم. ليس لدينا أدلة كافية لنقول أن متوسط وزن السلاحف بين هاتين المجموعتين مختلف.
ملحوظة: يمكنك أيضًا إجراء اختبار t المكون من عينتين بالكامل باستخدام حاسبة اختبار t المكونة من عينتين .
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية إجراء اختبار t المكون من عينتين باستخدام برامج إحصائية مختلفة:
كيفية إجراء اختبار t من عينتين في برنامج Excel
كيفية إجراء اختبار t لعينتين في برنامج SPSS
كيفية إجراء اختبار t من عينتين في Stata
كيفية إجراء اختبار t لعينتين في R
كيفية إجراء اختبار t من عينتين في بايثون
كيفية إجراء اختبار t من عينتين على الآلة الحاسبة TI-84
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر