الافتراضات الأربعة للانحدار الخطي

يعد الانحدار الخطي طريقة إحصائية مفيدة يمكننا استخدامها لفهم العلاقة بين متغيرين، x وy. ومع ذلك، قبل إجراء الانحدار الخطي، يجب علينا أولاً التأكد من استيفاء أربعة افتراضات:

1. العلاقة الخطية: توجد علاقة خطية بين المتغير المستقل x والمتغير التابع y.

2. الاستقلال: البقايا مستقلة. وعلى وجه الخصوص، لا يوجد ارتباط بين المخلفات المتتالية في بيانات السلاسل الزمنية.

3. المثلية: البقايا لها تباين ثابت عند كل مستوى من x.

4. الحالة الطبيعية: يتم توزيع بقايا النموذج بشكل طبيعي.

إذا لم يتم استيفاء واحد أو أكثر من هذه الافتراضات، فإن نتائج الانحدار الخطي قد تكون غير موثوقة أو حتى مضللة.

ونقدم في هذا المقال شرحًا لكل افتراض، وكيفية تحديد ما إذا كان الافتراض قد تحقق، وماذا تفعل إذا لم يتم استيفاء الافتراض.

الفرضية 1: العلاقة الخطية

توضيح

الافتراض الأول للانحدار الخطي هو أن هناك علاقة خطية بين المتغير المستقل x والمتغير المستقل y.

كيفية تحديد ما إذا كان هذا الافتراض قد تم استيفاءه

إن أبسط طريقة لاكتشاف ما إذا كان هذا الافتراض قد تم استيفاءه هو إنشاء مخطط مبعثر لـ x مقابل y. يتيح لك ذلك معرفة ما إذا كانت هناك علاقة خطية بين المتغيرين بشكل مرئي. إذا ظهر أن النقاط على المخطط يمكن أن تقع على طول خط مستقيم، فهذا يعني أن هناك نوعًا من العلاقة الخطية بين المتغيرين وقد تحقق هذا الافتراض.

على سبيل المثال، تظهر النقاط في الرسم البياني أدناه وكأنها تقع على خط مستقيم، مما يشير إلى وجود علاقة خطية بين x وy:

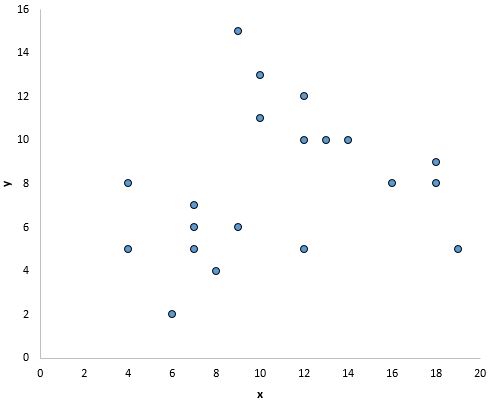
ومع ذلك، لا يبدو أن هناك علاقة خطية بين x وy في الرسم البياني أدناه:

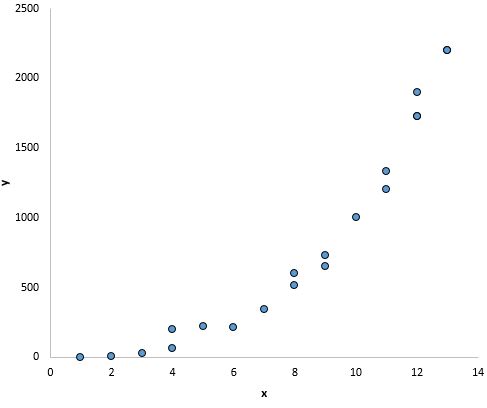
وفي هذا الرسم البياني يبدو أن هناك علاقة واضحة بين x وy، ولكنها ليست علاقة خطية :

ماذا تفعل إذا لم يتم احترام هذا الافتراض

إذا قمت بإنشاء مخطط مبعثر لقيم x وy ووجدت أنه لا توجد علاقة خطية بين المتغيرين، فلديك عدة خيارات:

1. قم بتطبيق تحويل غير خطي على المتغير المستقل و/أو التابع. تتضمن الأمثلة الشائعة أخذ السجل أو الجذر التربيعي أو المقلوب للمتغير المستقل و/أو التابع.

2. قم بإضافة متغير مستقل آخر إلى النموذج. على سبيل المثال، إذا كان الرسم البياني x مقابل y له شكل مكافئ، فقد يكون من المنطقي إضافة X ² كمتغير مستقل إضافي في النموذج.

الفرضية 2: الاستقلال

توضيح

الافتراض التالي للانحدار الخطي هو أن البقايا مستقلة. وهذا مهم بشكل خاص عند العمل مع بيانات السلاسل الزمنية. من الناحية المثالية، لا نريد أن يكون هناك اتجاه بين البقايا المتتالية. على سبيل المثال، يجب ألا تتزايد البقايا بشكل مستمر مع مرور الوقت.

كيفية تحديد ما إذا كان هذا الافتراض قد تم استيفاءه

إن أبسط طريقة لاختبار ما إذا كان هذا الافتراض صحيحًا هو النظر إلى مخطط السلاسل الزمنية للبقايا، وهو مخطط للبقايا مقابل الوقت. من الناحية المثالية، ينبغي أن تقع معظم الارتباطات الذاتية المتبقية ضمن نطاقات الثقة 95% حول الصفر، والتي تقع تقريبًا +/- 2 على الجذر التربيعي لـ n ، حيث n هو حجم العينة. يمكنك أيضًا اختبار ما إذا كان هذا الافتراض قد تم تحقيقه رسميًا باستخدام اختبار Durbin-Watson .

ماذا تفعل إذا لم يتم احترام هذا الافتراض

اعتمادًا على كيفية انتهاك هذا الافتراض، لديك عدة خيارات:

• للحصول على ارتباط تسلسلي إيجابي، فكر في إضافة فترات تأخر المتغير التابع و/أو المستقل إلى النموذج.
• بالنسبة للارتباط التسلسلي السلبي، تأكد من عدم تأخر أي من متغيراتك بشكل زائد .
• بالنسبة للارتباط الموسمي، فكر في إضافة نماذج موسمية إلى النموذج.

الفرضية 3: المثلية الجنسية

توضيح

الافتراض التالي للانحدار الخطي هو أن البقايا لها تباين ثابت عند كل مستوى من x. وهذا ما يسمى المثلية . عندما لا يكون الأمر كذلك، فإن البقايا تعاني من عدم تجانسها .

عندما تكون التغايرية موجودة في تحليل الانحدار، يصبح من الصعب تصديق نتائج التحليل. على وجه التحديد، تزيد التغايرية من التباين في تقديرات معامل الانحدار، لكن نموذج الانحدار لا يأخذ في الاعتبار ذلك. وهذا يجعل من الأرجح أن يدعي نموذج الانحدار أن المصطلح الموجود في النموذج له دلالة إحصائية، في حين أنه ليس كذلك في الواقع.

كيفية تحديد ما إذا كان هذا الافتراض قد تم استيفاءه

أسهل طريقة لاكتشاف التغايرية هي إنشاء قيمة مناسبة/مؤامرة متبقية .

بمجرد ملاءمة خط الانحدار لمجموعة بيانات، يمكنك إنشاء مخطط تبعثر يوضح القيم المجهزة للنموذج مقابل القيم المتبقية لتلك القيم المجهزة. يُظهر مخطط التشتت أدناه مخططًا نموذجيًا للقيمة المجهزة مقابل القيمة المتبقية التي توجد فيها التغايرية.

لاحظ كيف تنتشر البقايا أكثر فأكثر مع زيادة القيم المجهزة. هذا الشكل “المخروطي” هو علامة كلاسيكية على التغايرية:

ماذا تفعل إذا لم يتم احترام هذا الافتراض

هناك ثلاث طرق شائعة لتصحيح عدم التجانس:

1. تحويل المتغير التابع. التحويل الشائع هو ببساطة أخذ سجل المتغير التابع. على سبيل المثال، إذا استخدمنا حجم السكان (متغير مستقل) للتنبؤ بعدد بائعي الزهور في مدينة ما (متغير تابع)، فيمكننا بدلاً من ذلك محاولة استخدام حجم السكان للتنبؤ بلوغاريتم عدد بائعي الزهور في مدينة ما. غالبًا ما يؤدي استخدام سجل المتغير التابع، بدلاً من المتغير التابع الأصلي، إلى اختفاء التغايرية.

2. إعادة تعريف المتغير التابع. إحدى الطرق الشائعة لإعادة تعريف المتغير التابع هي استخدام المعدل بدلاً من القيمة الأولية. على سبيل المثال، بدلاً من استخدام حجم السكان للتنبؤ بعدد بائعي الزهور في المدينة، يمكننا استخدام حجم السكان للتنبؤ بعدد بائعي الزهور للفرد. في معظم الحالات، يؤدي هذا إلى تقليل التباين الذي يحدث بشكل طبيعي ضمن مجموعات سكانية أكبر نظرًا لأننا نقيس عدد بائعي الزهور لكل شخص، بدلاً من عدد بائعي الزهور نفسه.

3. استخدم الانحدار المرجح. هناك طريقة أخرى لتصحيح التغايرية وهي استخدام الانحدار المرجح. يقوم هذا النوع من الانحدار بتعيين وزن لكل نقطة بيانات بناءً على تباين قيمتها المجهزة. بشكل أساسي، يعطي هذا أوزانًا منخفضة لنقاط البيانات التي تحتوي على تباينات أعلى، مما يقلل من مربعاتها المتبقية. عند استخدام الأوزان المناسبة، يمكن أن يؤدي ذلك إلى القضاء على مشكلة عدم التجانس.

الفرضية 4: الحياة الطبيعية

توضيح

الافتراض التالي للانحدار الخطي هو أن البقايا يتم توزيعها بشكل طبيعي.

كيفية تحديد ما إذا كان هذا الافتراض قد تم استيفاءه

هناك طريقتان شائعتان للتحقق من استيفاء هذا الافتراض:

1. تحقق بصريًا من الفرضية باستخدام مخططات QQ .

مخطط QQ، وهو اختصار لمخطط الكم الكمي، هو نوع من المخطط الذي يمكننا استخدامه لتحديد ما إذا كانت بقايا النموذج تتبع التوزيع الطبيعي أم لا. إذا كانت النقاط الموجودة على قطعة الأرض تشكل خطًا قطريًا مستقيمًا تقريبًا، فإن افتراض الحالة الطبيعية قد تحقق.

يُظهر مخطط QQ التالي مثالاً على المخلفات التي تتبع تقريبًا التوزيع الطبيعي:

ومع ذلك، فإن مخطط QQ أدناه يوضح مثالاً لحالة تنحرف فيها البقايا بوضوح عن خط قطري مستقيم، مما يشير إلى أنها لا تتبع التوزيع الطبيعي:

2. يمكنك أيضًا التحقق من افتراض الحالة الطبيعية باستخدام الاختبارات الإحصائية الرسمية مثل Shapiro-Wilk، أو Kolmogorov-Smironov، أو Jarque-Barre، أو D’Agostino-Pearson. ومع ذلك، ضع في اعتبارك أن هذه الاختبارات حساسة لأحجام العينات الكبيرة – أي أنها غالبًا ما تستنتج أن المخلفات ليست طبيعية عندما يكون حجم العينة كبيرًا. ولهذا السبب غالبًا ما يكون من الأسهل استخدام الأساليب الرسومية مثل مخطط QQ للتحقق من هذه الفرضية.

ماذا تفعل إذا لم يتم احترام هذا الافتراض

إذا لم يتم استيفاء افتراض الحالة الطبيعية، فلديك عدة خيارات:

• أولاً، تأكد من أن القيم المتطرفة ليس لها تأثير كبير على التوزيع. إذا كان هناك أي قيم متطرفة، فتأكد من أنها قيم حقيقية وليست أخطاء في إدخال البيانات.
• ثم يمكنك تطبيق تحويل غير خطي على المتغير المستقل و/أو التابع. تتضمن الأمثلة الشائعة أخذ السجل أو الجذر التربيعي أو المقلوب للمتغير المستقل و/أو التابع.

قراءة متعمقة:

مقدمة إلى الانحدار الخطي البسيط
فهم التغايرية في تحليل الانحدار
كيفية إنشاء وتفسير مؤامرة QQ في R