فرضية التباين المستمر: التعريف والمثال
الانحدار الخطي هو أسلوب نستخدمه لتحديد العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة .
أحد الافتراضات الرئيسية للانحدار الخطي هو أن البقايا لها تباين ثابت في كل مستوى من متغير (متغيرات) التوقع.
إذا لم يتم التحقق من هذا الافتراض، فإن البقايا ستعاني من عدم تجانسها . وعندما يحدث هذا، تصبح تقديرات معامل النموذج غير موثوقة.
كيفية تقييم التباين المستمر
الطريقة الأكثر شيوعًا لتحديد ما إذا كانت بقايا نموذج الانحدار لها تباين ثابت هي إنشاء مخطط للقيم المجهزة مقابل القيم المتبقية .
هذا نوع من المخططات التي تعرض القيم المجهزة لنموذج الانحدار على طول المحور السيني وبقايا تلك القيم المجهزة على طول المحور الصادي.
إذا كان توزيع البقايا متساويا تقريبا عند كل مستوى من القيم المجهزة، فإننا نقول أن افتراض التباين الثابت قد تحقق.
وبخلاف ذلك، إذا زاد تشتت المخلفات أو انخفض بشكل منهجي، فمن المحتمل أن يتم انتهاك هذا الافتراض.
ملاحظة : لا يمكن إنشاء هذا النوع من المخططات إلا بعد ملاءمة نموذج الانحدار لمجموعة البيانات.
يوضح الرسم البياني التالي مثالاً لمخطط القيم المجهزة مقابل القيم المتبقية الذي يعرض التباين الثابت :
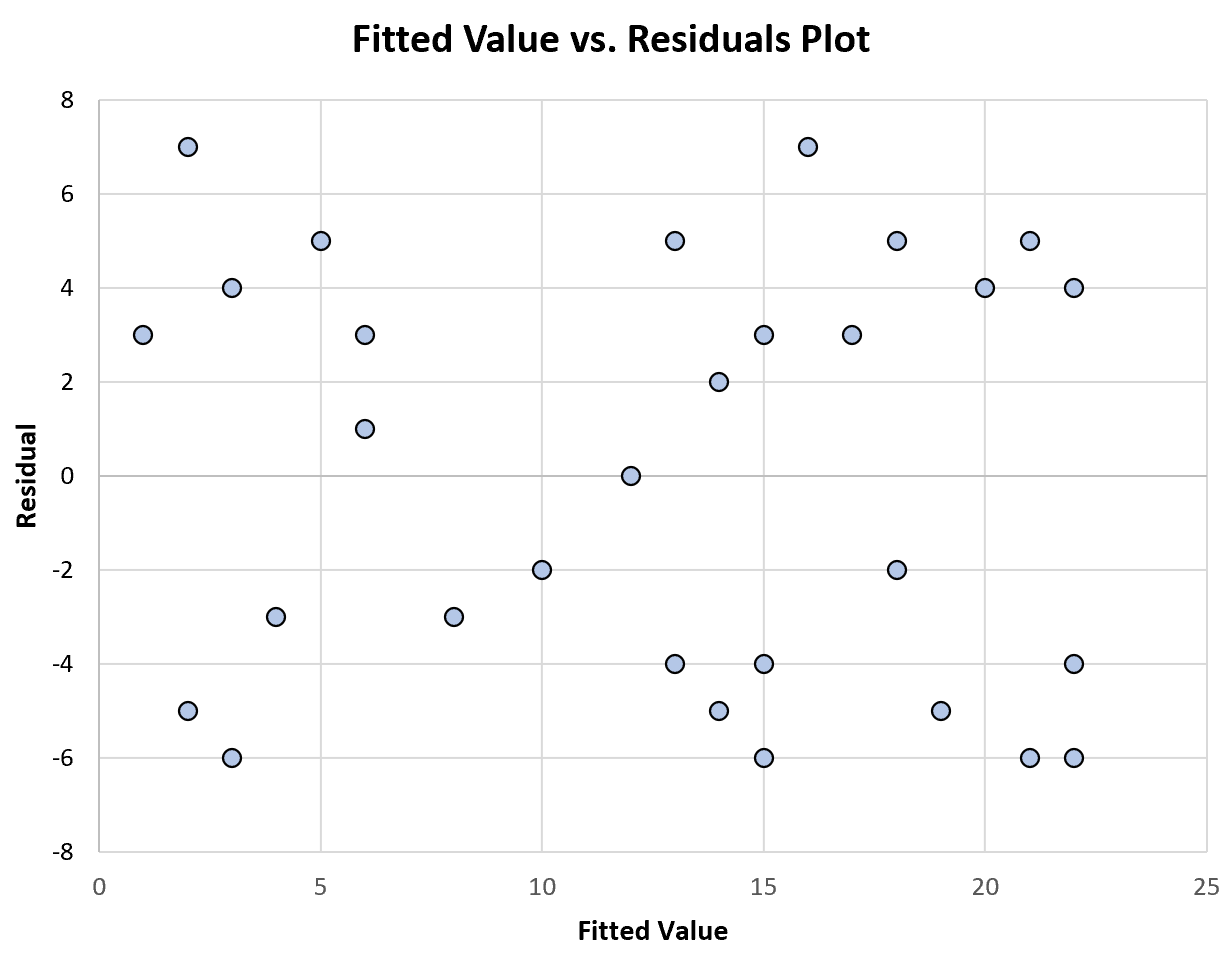
لاحظ كيف أن البقايا متناثرة بشكل عشوائي حول الصفر، دون أي نمط معين، مع تباين ثابت تقريبًا عند كل مستوى من القيم المجهزة.
يوضح الرسم البياني التالي مثالاً لمخطط القيم المجهزة مقابل القيم المتبقية الذي يعرض التباين غير الثابت :
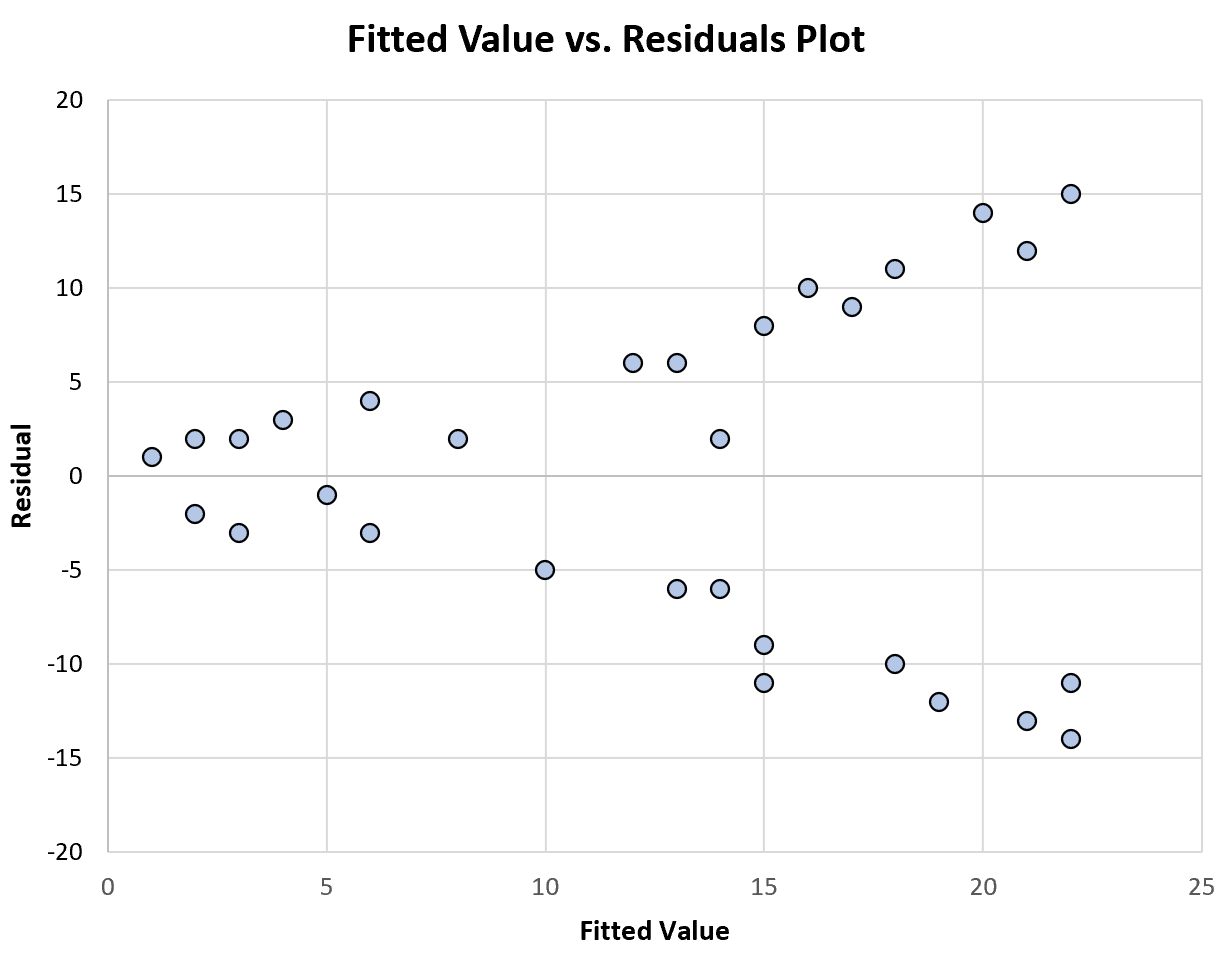
لاحظ أن توزيع البقايا يصبح أكبر مع زيادة القيم المجهزة. هذه علامة نموذجية على التباين غير الثابت.
يخبرنا هذا أن نموذج الانحدار الخاص بنا يعاني من تباين غير ثابت في القيم المتبقية، وبالتالي فإن تقديرات معامل النموذج غير موثوقة.
كيفية إصلاح انتهاك التباين المستمر
إذا تم انتهاك افتراض التباين الثابت، فإن الطريقة الأكثر شيوعًا لحل هذه المشكلة هي تحويل متغير الاستجابة باستخدام أحد التحويلات الثلاثة:
1. تحويل السجل: تحويل متغير الاستجابة من y إلى log(y)
2. تحويل الجذر التربيعي: تحويل متغير الاستجابة من y إلى √y
3. تحويل الجذر التكعيبي: تحويل متغير الاستجابة من y إلى y 1/3
وبإجراء هذه التحويلات تختفي مشكلة التباين غير الثابت بشكل عام.
مصادر إضافية
توفر البرامج التعليمية التالية معلومات إضافية حول الانحدار الخطي والتحليل المتبقي:
مقدمة إلى الانحدار الخطي البسيط
مقدمة في الانحدار الخطي المتعدد
الافتراضات الأربعة للانحدار الخطي
ما هي البقايا في الإحصاء؟