الاحتمال الخلفي: تعريف + مثال

الاحتمال البعدي هو الاحتمال المحدث لحدوث حدث بعد أخذ المعلومات الجديدة في الاعتبار.

على سبيل المثال، قد نكون مهتمين باحتمال وقوع الحدث “أ” بعد حساب الحدث “ب” الذي وقع للتو. يمكننا حساب هذا الاحتمال الخلفي باستخدام الصيغة التالية:

ف(أ|ب) = ف(أ) * ف(ب|أ) / ف(ب)

ذهب:

P(A|B) = احتمال وقوع الحدث A، بشرط وقوع الحدث B. لاحظ أن “| » تعني “معطى”.

P(A) = احتمال وقوع الحدث A.

P(B) = احتمال وقوع الحدث B.

P(B|A) = احتمال وقوع الحدث B، بشرط وقوع الحدث A.

مثال: حساب الاحتمال الخلفي

تتكون الغابة من 20% من أشجار البلوط و80% من خشب القيقب. لنفترض أننا نعلم أن 90% من أشجار البلوط تتمتع بصحة جيدة بينما 50% فقط من أشجار القيقب تتمتع بصحة جيدة. لنفترض، من بعيد، أنه يمكنك معرفة أن شجرة معينة سليمة. ما هو احتمال أن تكون الشجرة بلوط؟

تذكر أن احتمال وقوع الحدث A بشرط وقوع الحدث B هو:

ف(أ|ب) = ف(أ) * ف(ب|أ) / ف(ب)

في هذا المثال، احتمال أن تكون الشجرة بلوطًا بشرط أن تكون الشجرة سليمة هو:

P(بلوط|صحي) = P(بلوط) * P(صحي|بلوط) / P(صحي)

P(Oak) = احتمال أن تكون شجرة معينة بلوطًا هو 0.2 لأن 20% من جميع الأشجار في الغابة هي بلوط.

P(صحية) = يمكن حساب احتمالية أن تكون شجرة معينة صحية على النحو التالي: (0.20)*(0.9) + (0.8)*(0.5) = 0.58 .

P(Healthy|Oak) = احتمال أن تكون الشجرة صحية نظرًا لأنها بلوط هو 0.9 ، حيث قيل لنا أن 90% من أشجار البلوط صحية.

باستخدام هذه الأرقام الثلاثة، يمكننا إيجاد احتمال أن تكون الشجرة بلوطًا بشرط أن تكون صحية:

P(بلوط|صحي) = P(بلوط) * P(صحي|بلوط) / P(صحي) = (0.2) * (0.9) / (0.58) = 0.3103 .

للحصول على فهم بديهي لهذا الاحتمال، لنفترض أن الشبكة التالية تمثل هذه الغابة المكونة من 100 شجرة. بالضبط 20 شجرة من أشجار البلوط و 18 منها صحية. أما الـ 80 شجرة الأخرى فهي من أشجار القيقب و40 منها سليمة.

(O = البلوط، M = خشب القيقب، الأخضر = صحي، الأحمر = غير صحي)

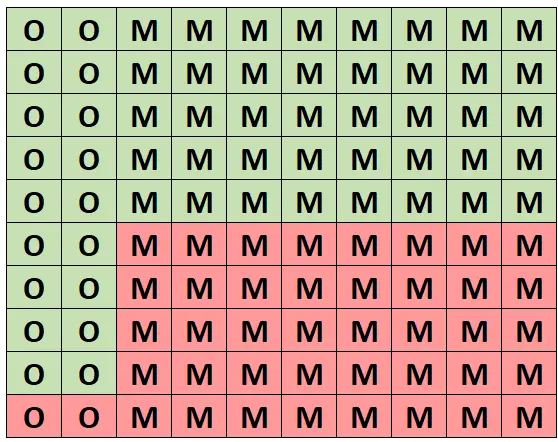
من بين جميع الأشجار، 58 منها سليمة و18 منها من أشجار البلوط. لذا، إذا علمنا أننا اخترنا شجرة صحية، فإن احتمال أن تكون شجرة بلوط هو 18/58 = 0.3103 .

متى يجب عليك استخدام الاحتمال الخلفي؟

يُستخدم الاحتمال الخلفي في مجموعة واسعة من المجالات، بما في ذلك التمويل والطب والاقتصاد والتنبؤ بالطقس.

الهدف من استخدام الاحتمالات الخلفية هو تحديث الاعتقاد السابق الذي كان لدينا حول شيء ما بمجرد حصولنا على معلومات جديدة.

تذكر من المثال السابق أننا عرفنا أن احتمال أن تكون شجرة معينة في الغابة من خشب البلوط هو 20%. وهذا ما يسمى الاحتمال المسبق . إذا اخترنا شجرة عشوائيًا، فسنعرف أن احتمال أن تكون شجرة بلوط هو 0.20.

ومع ذلك، بمجرد حصولنا على المعلومات الجديدة التي تفيد بأن الشجرة التي اخترناها كانت صحية، تمكنا من استخدام هذه المعلومات الجديدة لتحديد أن الاحتمال الخلفي لهذه الشجرة هي شجرة بلوط هو 0.3103 بدلاً من ذلك.

في العالم الحقيقي، يكتشف الناس باستمرار معلومات جديدة. تساعدنا هذه المعلومات الجديدة على تحديث معتقداتنا السابقة. من الناحية الإحصائية، هذا يعني أننا قادرون على توليد احتمالات خلفية للأحداث التي تحدث، مما يساعدنا على اكتساب فهم أكثر دقة للعالم ويسمح لنا بعمل تنبؤات أكثر دقة حول الأحداث المستقبلية.