كيفية إجراء الانحدار التربيعي في spss

عندما يكون بين متغيرين علاقة خطية، يمكنك غالبًا استخدام الانحدار الخطي البسيط لتحديد العلاقة بينهما.

ومع ذلك، فإن الانحدار الخطي البسيط لا يعمل بشكل جيد عندما يكون بين متغيرين علاقة غير خطية. في هذه الحالات، يمكنك محاولة استخدام الانحدار التربيعي .

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار التربيعي في برنامج SPSS.

مثال: الانحدار التربيعي في SPSS

لنفترض أننا نريد أن نفهم العلاقة بين عدد ساعات العمل والسعادة. لدينا البيانات التالية عن عدد ساعات العمل أسبوعيًا ومستوى السعادة المُبلغ عنه (على مقياس من 0 إلى 100) لـ 16 شخصًا مختلفًا:

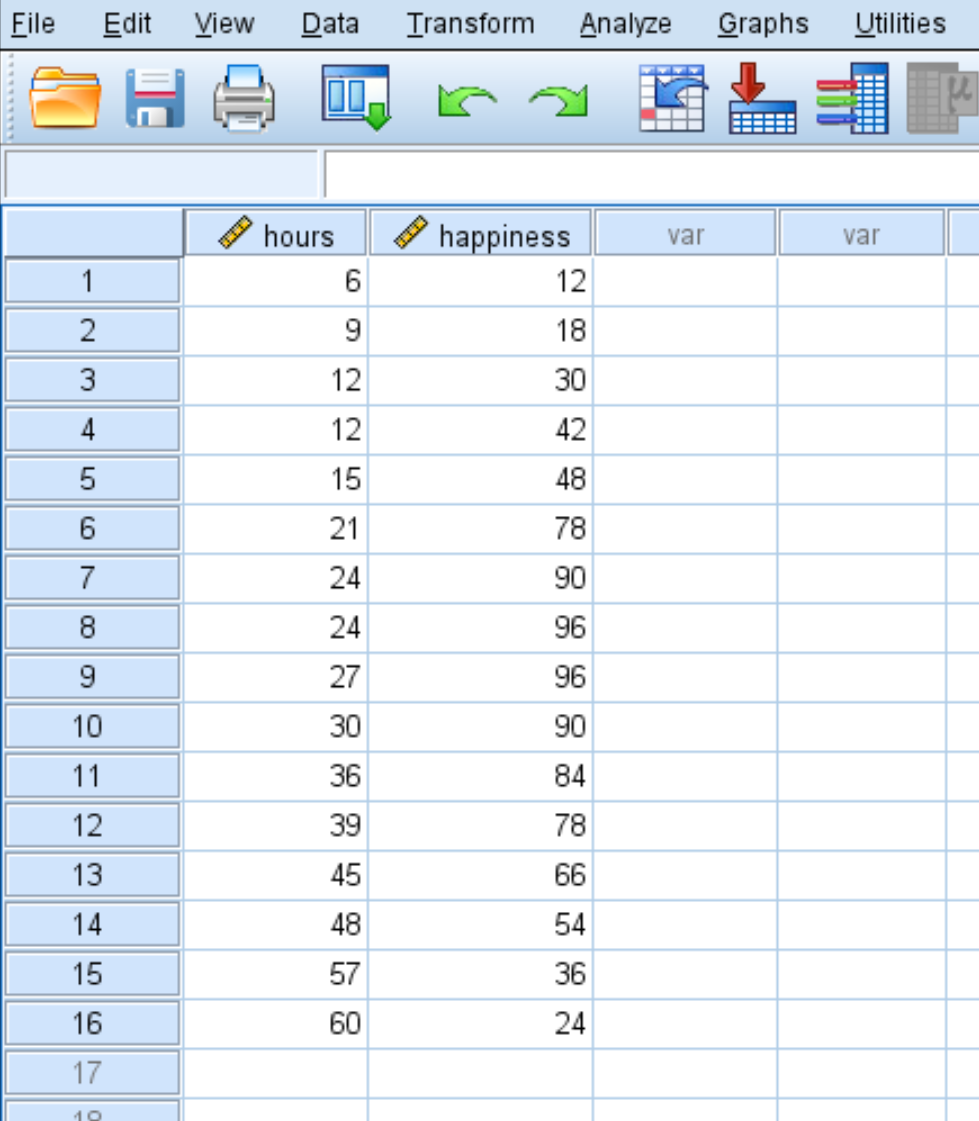
استخدم الخطوات التالية لإجراء الانحدار التربيعي في SPSS.

الخطوة 1: تصور البيانات.

قبل إجراء الانحدار التربيعي، دعونا ننشئ مخططًا مبعثرًا لتصور العلاقة بين ساعات العمل والسعادة للتحقق من أن المتغيرين لهما علاقة تربيعية بالفعل.

انقر فوق علامة التبويب “المخططات” ، ثم انقر فوق “منشئ المخططات” :

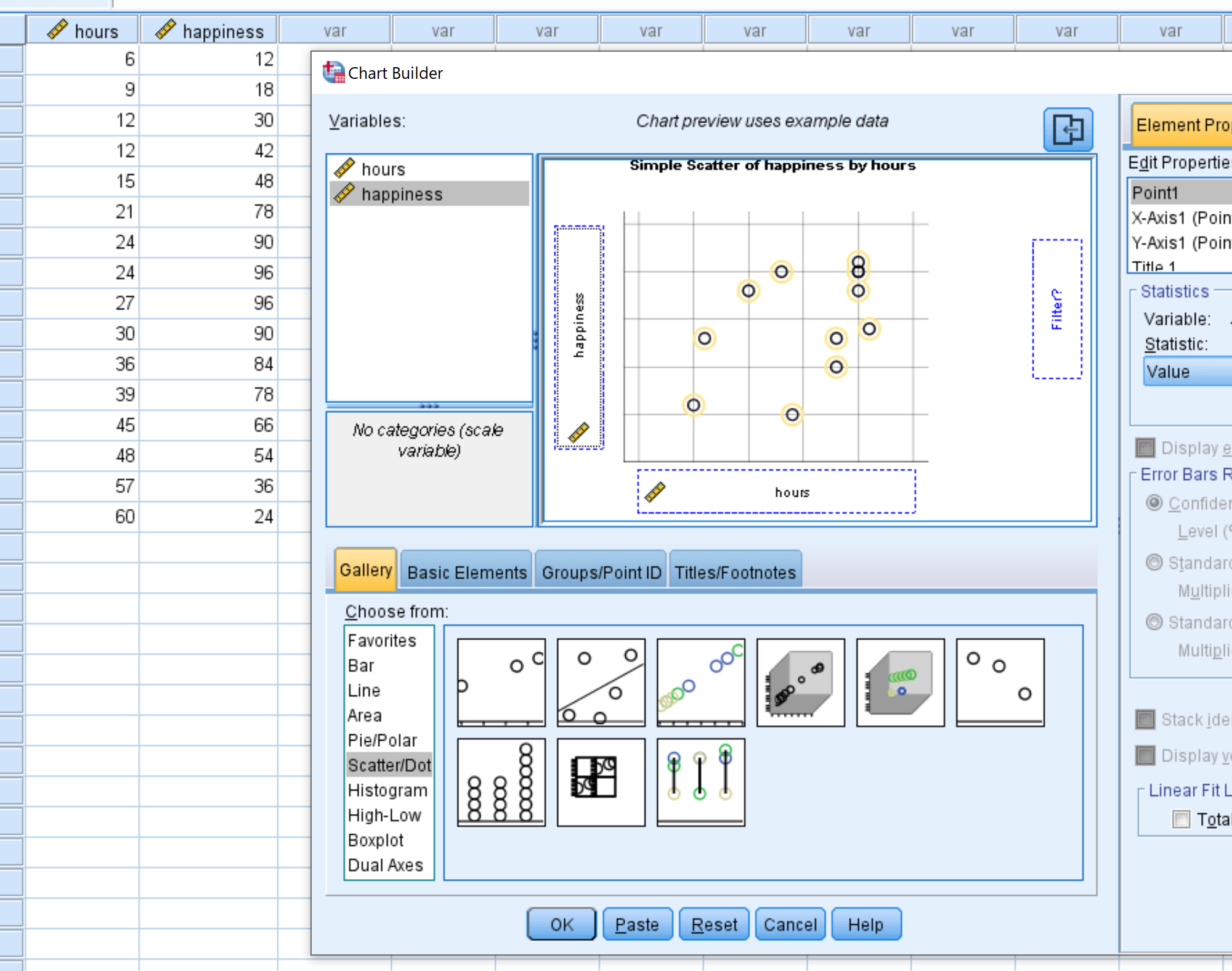
في النافذة الجديدة التي تظهر، اختر Scatter/Dot من قائمة اختر من . ثم اسحب المخطط المسمى Simple Scatter إلى نافذة التحرير الرئيسية. اسحب الساعات المتغيرة على المحور السيني والسعادة على المحور الصادي. ثم انقر فوق موافق .

ستظهر المخطط المبعثر التالي:

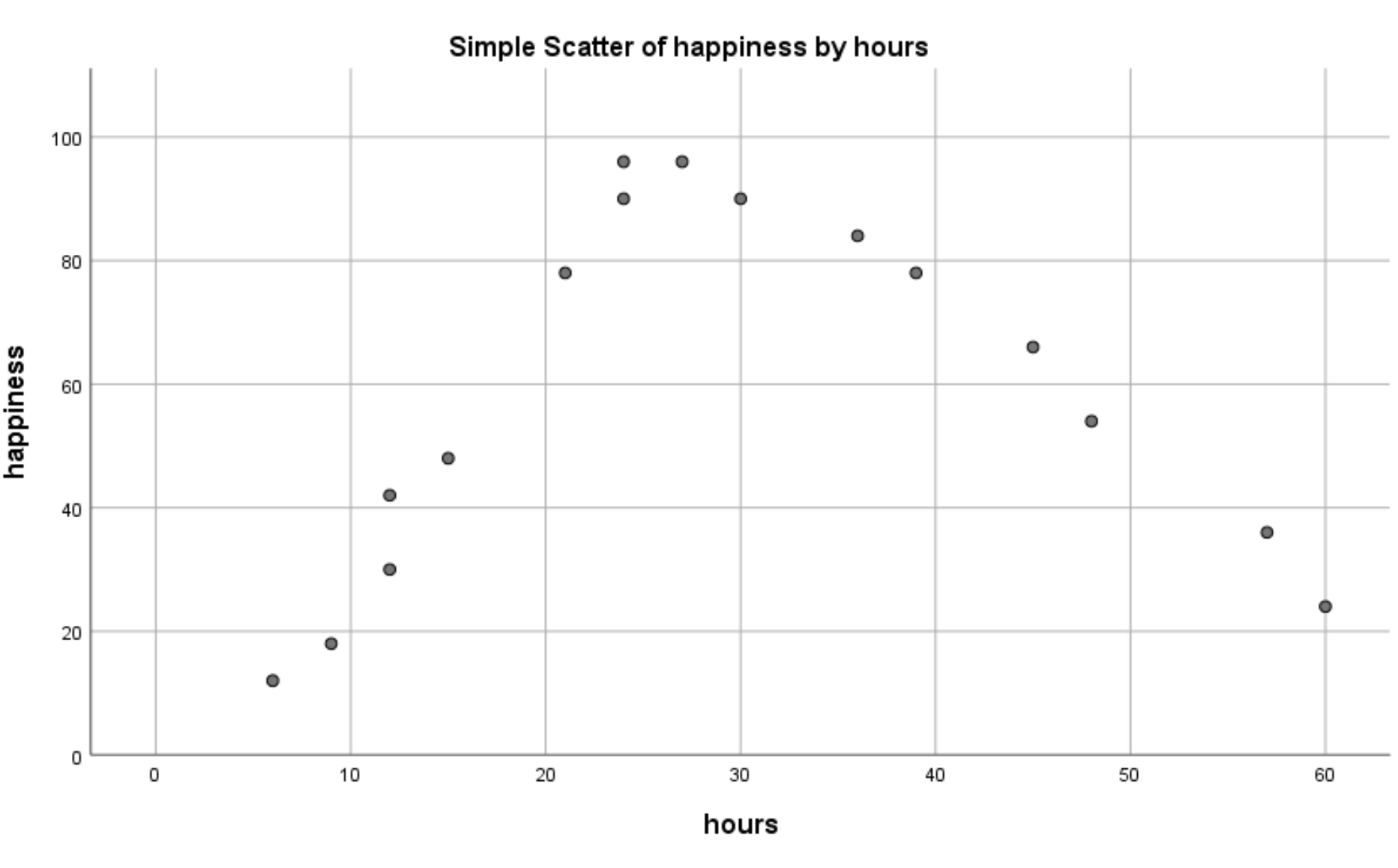
يمكننا أن نرى بوضوح أن هناك علاقة غير خطية بين ساعات العمل والسعادة. يخبرنا هذا أن الانحدار التربيعي هو أسلوب مناسب لاستخدامه في هذه الحالة.

الخطوة 2: إنشاء متغير جديد.

قبل أن نتمكن من إجراء الانحدار التربيعي، نحتاج إلى إنشاء متغير توقع للساعات ² .

انقر فوق علامة التبويب “التحويل” ، ثم انقر فوق “حساب المتغير” :

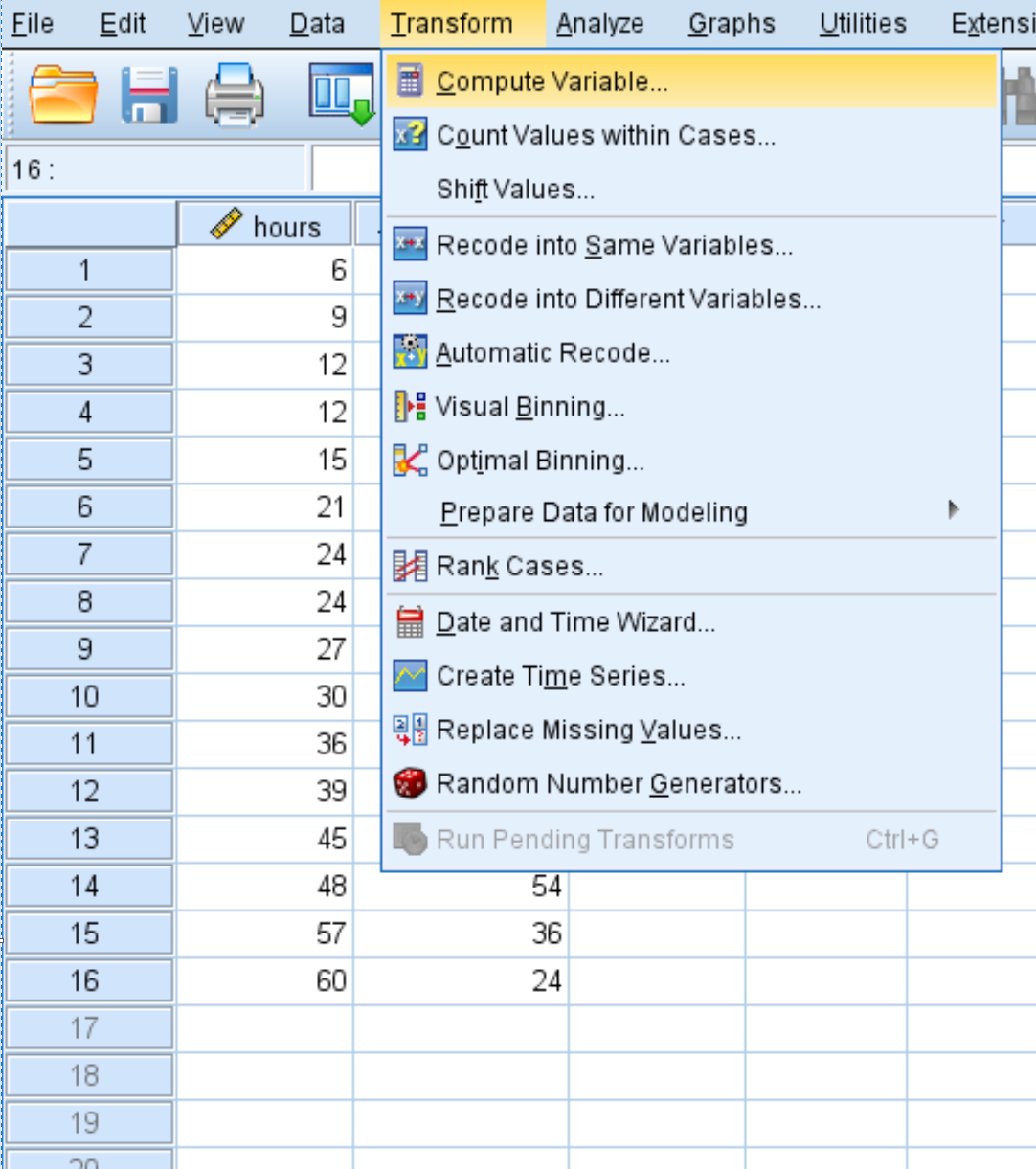
في النافذة الجديدة التي تظهر، قم بتسمية المتغير الهدف hours2 واضبطه على hours*hours :

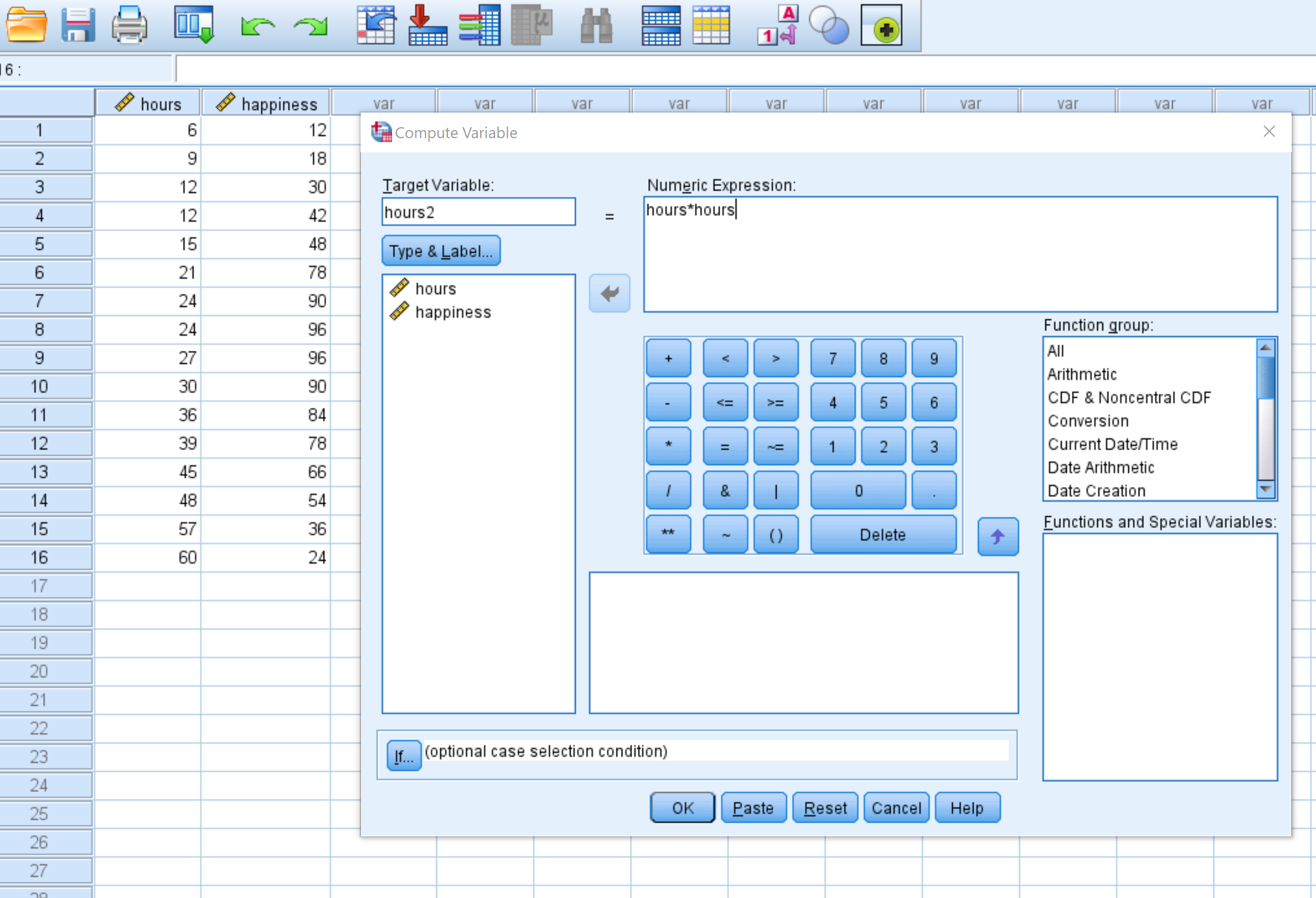
بمجرد النقر فوق موافق ، سيظهر المتغير hours2 في عمود جديد:

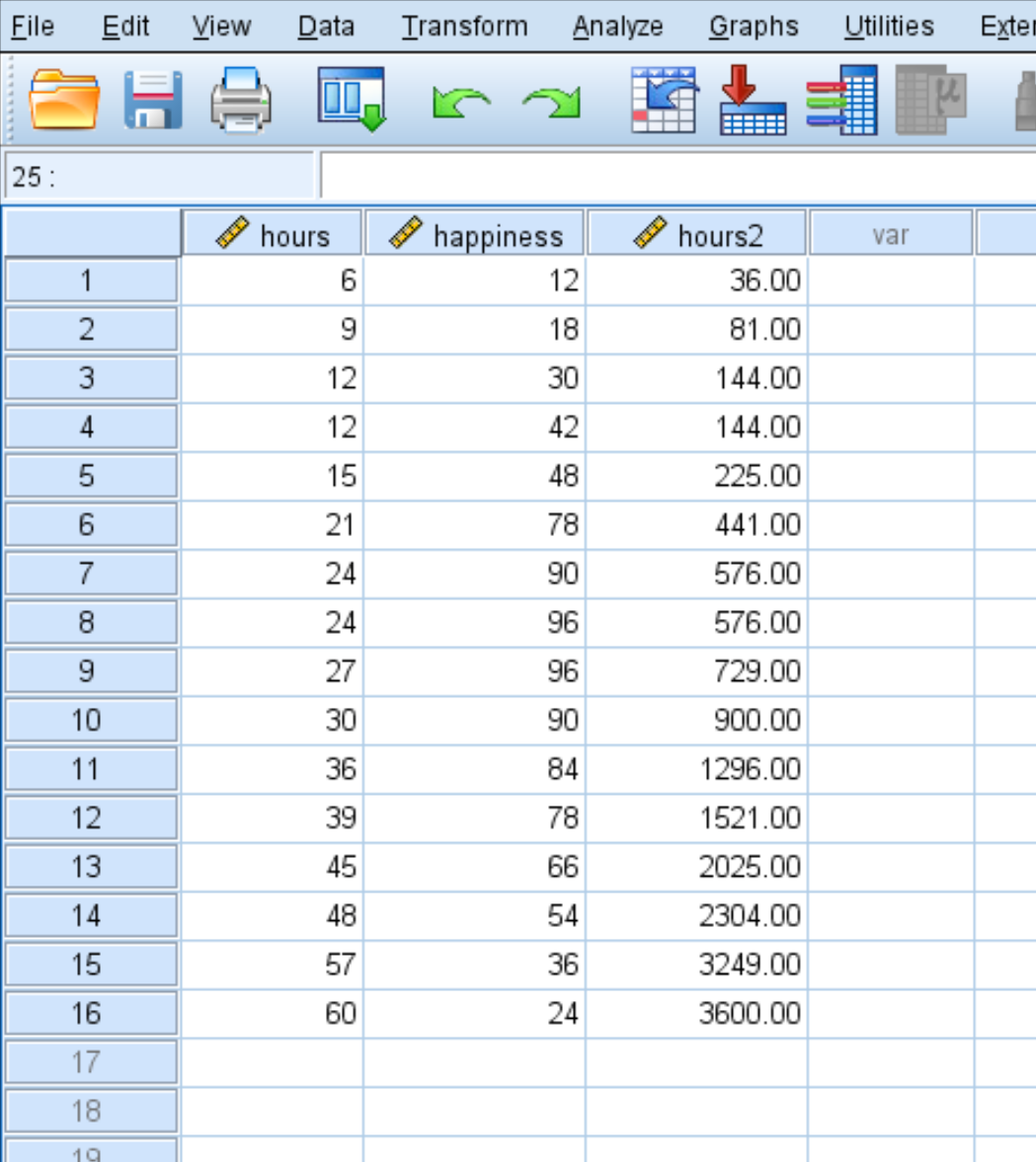
الخطوة 3: تنفيذ الانحدار التربيعي.

بعد ذلك، سوف نقوم بإجراء الانحدار التربيعي. انقر فوق علامة التبويب تحليل ، ثم الانحدار ، ثم الخطي :

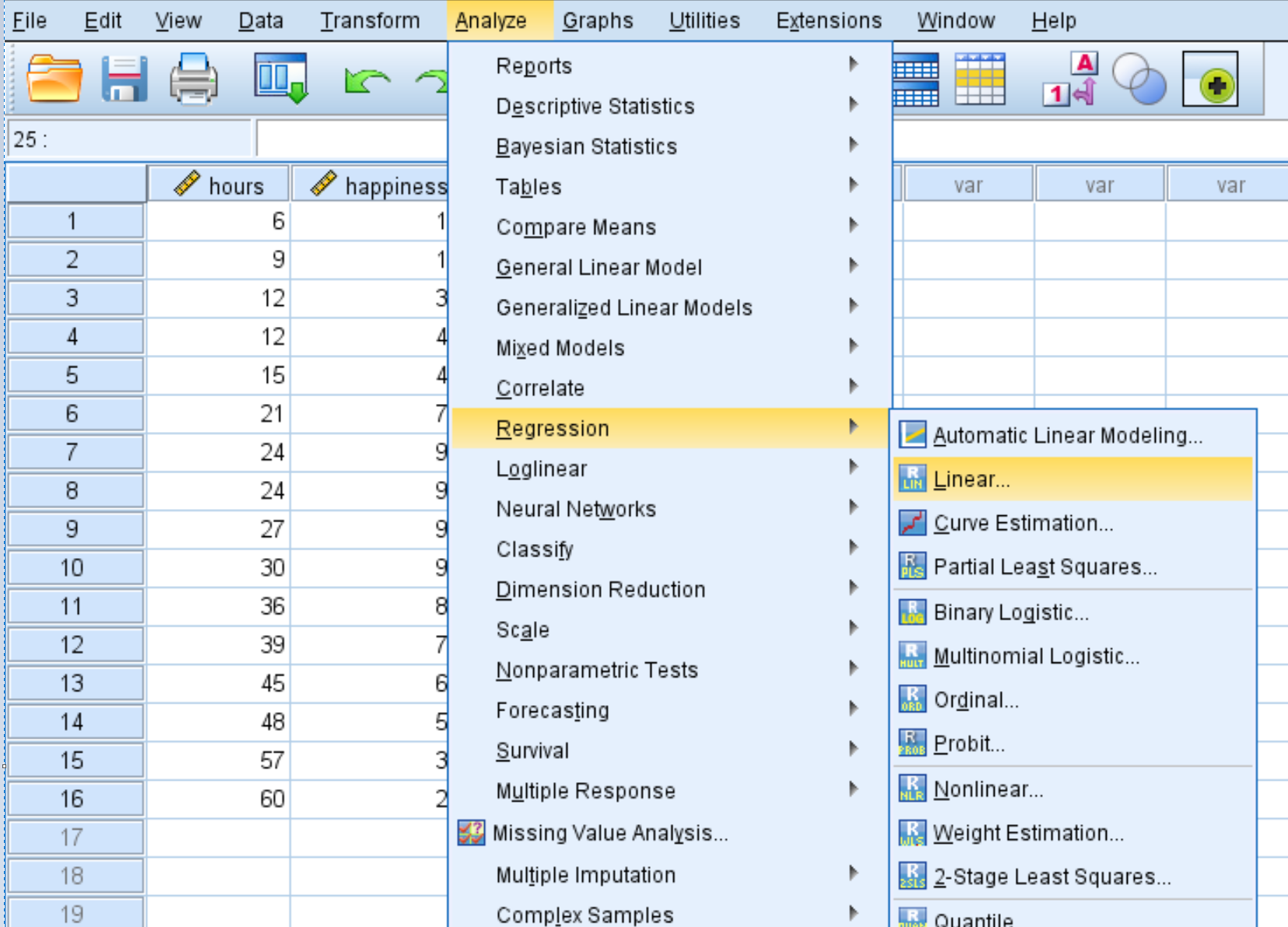
في النافذة الجديدة التي تظهر، اسحب السعادة إلى المربع المسمى “المعتمد”. اسحب Hours و Hours2 إلى المربع المسمى مستقل (مستقلون). ثم انقر فوق موافق .

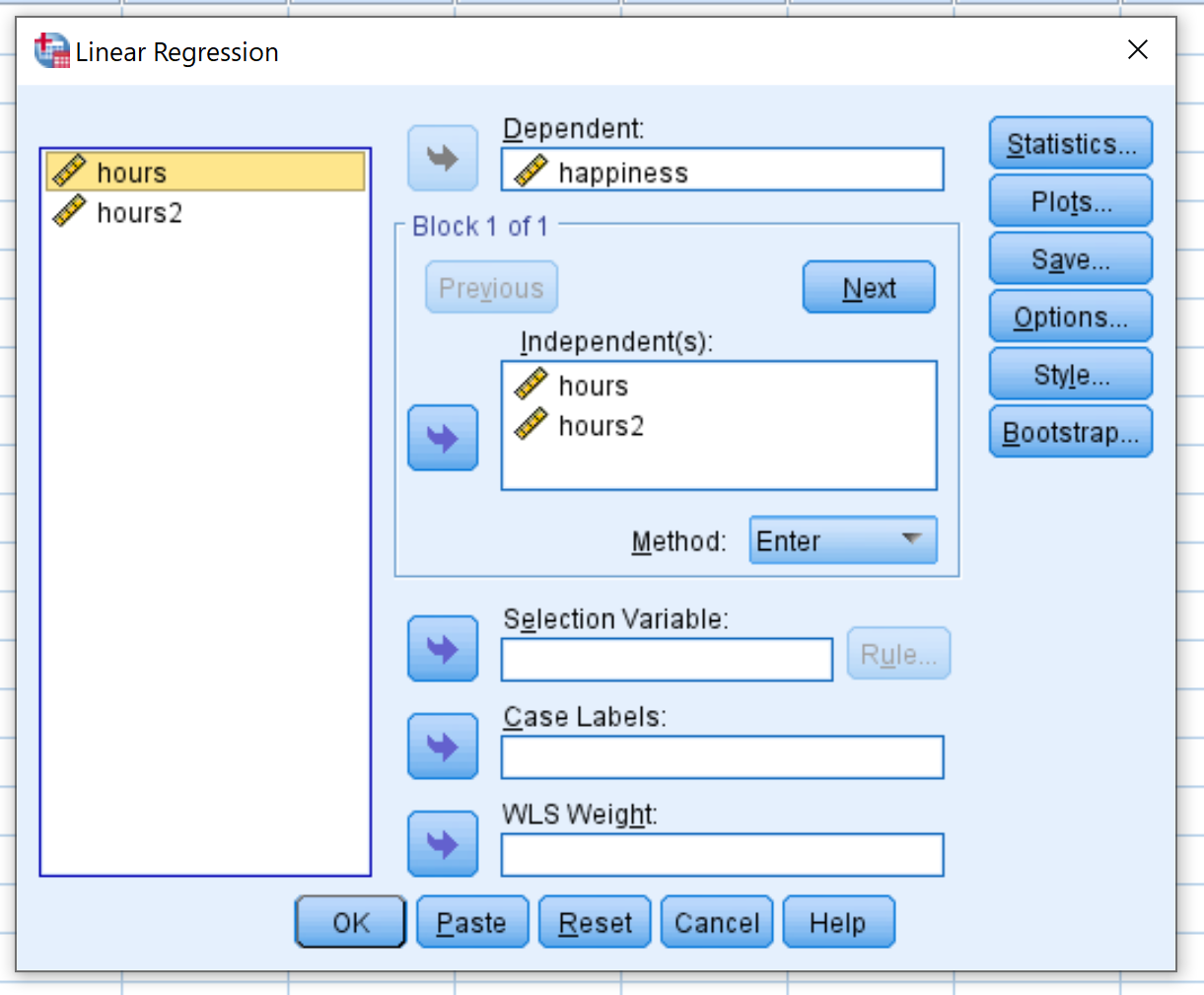
الخطوة 4: تفسير النتائج.

بمجرد النقر فوق “موافق” ، ستظهر نتائج الانحدار التربيعي في نافذة جديدة.

الجدول الأول الذي يهمنا يسمى ملخص النموذج :

فيما يلي كيفية تفسير الأرقام الأكثر صلة في هذا الجدول:

• مربع R: هو نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بالمتغيرات التوضيحية. في هذا المثال، يمكن تفسير 90.9% من التباين في السعادة من خلال متغيري الساعات والساعات ² .
• معيار. خطأ التقدير: الخطأ القياسي هو متوسط المسافة بين القيم المرصودة وخط الانحدار. في هذا المثال، تنحرف القيم المرصودة في المتوسط بمقدار 9519 وحدة عن خط الانحدار.

الجدول التالي الذي يهمنا يسمى ANOVA :

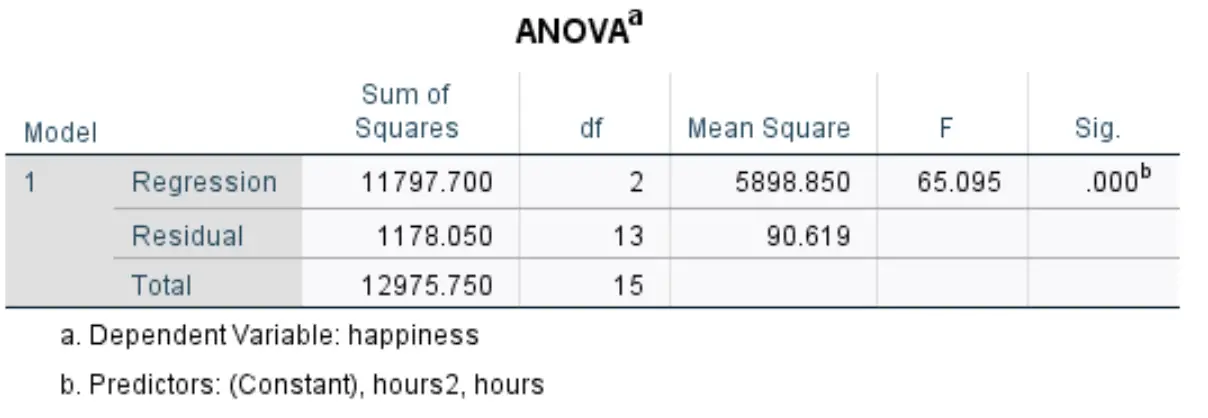
فيما يلي كيفية تفسير الأرقام الأكثر صلة في هذا الجدول:

• F: هذه هي إحصائية F الإجمالية لنموذج الانحدار، ويتم حسابها على أنها متوسط مربع الانحدار / متوسط المربع المتبقي.
• Sig: هذه هي القيمة p المرتبطة بإحصائيات F الإجمالية. يخبرنا هذا ما إذا كان نموذج الانحدار ككل ذو دلالة إحصائية أم لا. في هذه الحالة، تكون القيمة p تساوي 0.000، مما يشير إلى أن المتغيرات التوضيحية ساعات وساعات ² مجتمعة لها ارتباط ذو دلالة إحصائية بنتيجة الامتحان.

الجدول التالي الذي يهمنا هو بعنوان المعاملات :

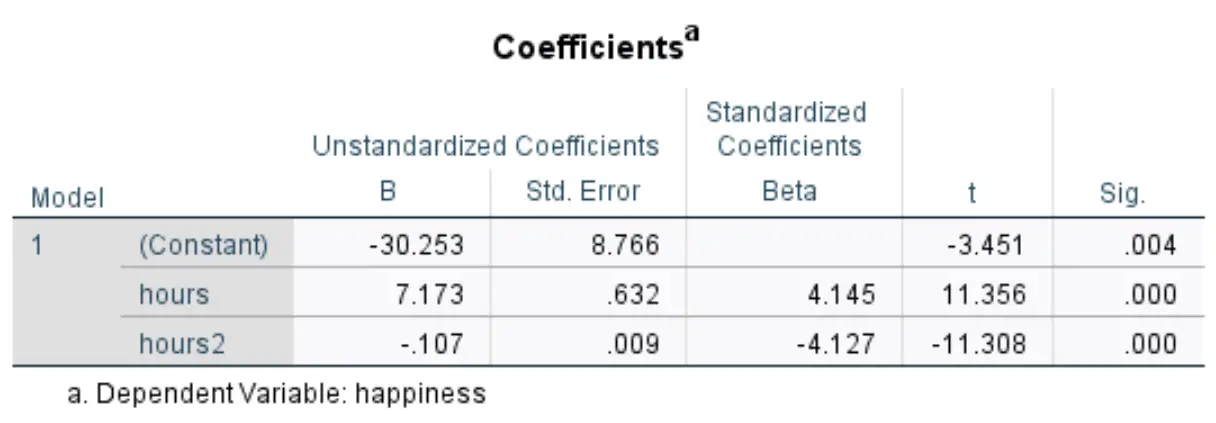
يمكننا استخدام القيم الموجودة في العمود Unstandardized B لتكوين معادلة الانحدار المقدرة لمجموعة البيانات هذه:

مستوى السعادة المقدر = -30.253 + 7.173*(ساعات) – 0.107*(ساعات ² )

يمكننا استخدام هذه المعادلة للعثور على مستوى السعادة المقدر للفرد بناءً على عدد ساعات العمل في الأسبوع. على سبيل المثال، الشخص الذي يعمل 60 ساعة في الأسبوع يجب أن يكون مستوى سعادته 14.97:

مستوى السعادة المقدر = -30.253 + 7.173*(60) – 0.107*(60 ² ) = 14.97 .

وعلى العكس من ذلك، فإن الشخص الذي يعمل 30 ساعة أسبوعيًا يجب أن يكون مستوى سعادته 88.65:

مستوى السعادة المقدر = -30.253 + 7.173*(30) – 0.107*(30 ² ) = 88.65 .

الخطوة 5: الإبلاغ عن النتائج.

وأخيرًا، نريد الإبلاغ عن نتائج الانحدار التربيعي. فيما يلي مثال لكيفية القيام بذلك:

تم إجراء الانحدار التربيعي لتحديد العلاقة بين عدد الساعات التي عمل فيها الفرد ومستوى سعادته المقابل (يقاس من 0 إلى 100). تم استخدام عينة من 16 شخصا في التحليل.

وأظهرت النتائج وجود علاقة ذات دلالة إحصائية بين المتغيرات التفسيرية ساعات وساعات ² ومتغير الاستجابة السعادة (F(2, 13) = 65.095, p <0.000).

يشكل هذان المتغيران التفسيريان معًا 90.9% من التباين في السعادة.

وتبين أن معادلة الانحدار هي:

مستوى السعادة المقدر = -30.253 + 7.173 (ساعة) – 0.107 ( ^ساعتان )