الانحدار الخطي البسيط
تشرح هذه المقالة ما هو الانحدار الخطي البسيط في الإحصائيات وكيفية تنفيذه. وبالمثل، ستجد حل تمرين الانحدار الخطي البسيط، بالإضافة إلى حاسبة الانحدار الخطي البسيطة عبر الإنترنت.
ما هو الانحدار الخطي البسيط؟
الانحدار الخطي البسيط هو نموذج إحصائي يستخدم لربط متغير مستقل ونحاول تقريب العلاقة بين المتغيرين.
لذلك، يتم استخدام الانحدار الخطي البسيط لإيجاد معادلة تربط بين متغيرين خطيًا. ومن الناحية المنطقية، يجب أن تكون العلاقة بين المتغيرين خطية، وإلا فيجب استخدام نوع آخر من نماذج الانحدار.
تتكون معادلة نموذج الانحدار الخطي البسيط من معاملين: ثابت المعادلة (ب 0 ) ومعامل الارتباط بين المتغيرين (ب 1 ). ولذلك، فإن معادلة نموذج الانحدار الخطي البسيط هي y=b 0 +b 1 x.
![]()
يتم رسم معادلة الانحدار الخطي البسيط كخط مستقيم، وبالتالي فإن المعامل b 0 هو التقاطع والمعامل b 1 هو ميل الخط.
صيغ الانحدار الخطي البسيطة
الصيغ لحساب معاملات الانحدار الخطي البسيط هي كما يلي:
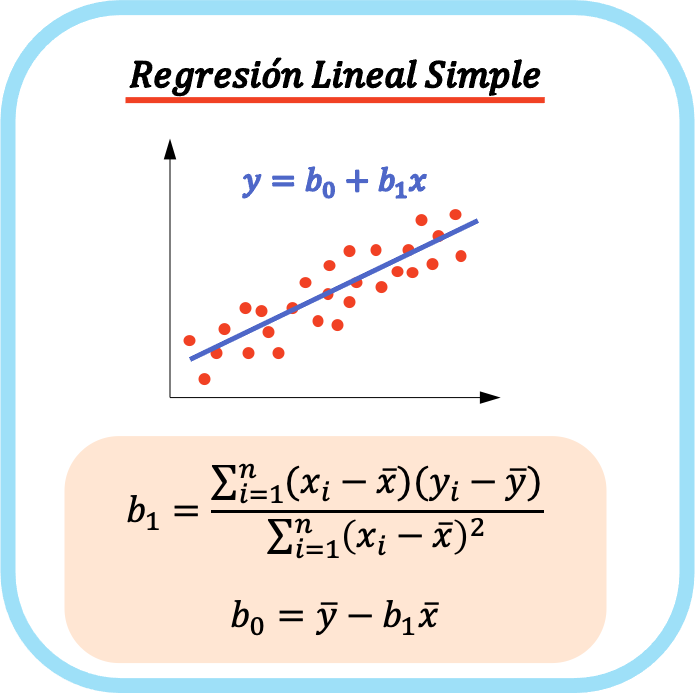
👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب معاملات الانحدار الخطي البسيط لأي مجموعة بيانات.
ومن الواضح أن المعادلة الناتجة عن نموذج الانحدار الخطي البسيط لن تكون قادرة على تخمين القيمة الدقيقة لجميع الملاحظات، حيث أن هذا النموذج يحاول ببساطة إيجاد معادلة تقريبية للعلاقة بين المتغيرين. وبالتالي، يتم تعريف المتبقي على أنه الفرق بين القيمة الحقيقية والقيمة المقدرة بواسطة نموذج الانحدار الخطي.
![]()
لاحظ أن الهدف من نموذج الانحدار الخطي البسيط هو تقليل مربعات القيم المتبقية، أي أن الانحدار الخطي البسيط يعتمد على معيار المربعات الصغرى .
مثال ملموس على الانحدار الخطي البسيط
للانتهاء من فهم طريقة الانحدار الخطي البسيط، إليك مثال عملي خطوة بخطوة يتم فيه حساب معادلة نموذج الانحدار الخطي البسيط من مجموعة من البيانات الإحصائية.
- بعد إجراء اختبار الإحصاء، سُئل خمسة طلاب عن عدد ساعات الدراسة التي خصصوها للامتحان. يتم عرض البيانات في الجدول أدناه. تنفيذ نموذج انحدار خطي بسيط للبيانات الإحصائية التي تم جمعها لربط ساعات الدراسة خطيًا بالصف الذي تم تحقيقه.

لتنفيذ نموذج الانحدار الخطي البسيط، يجب علينا تحديد المعاملين b 0 وb 1 للمعادلة، ولهذا يجب علينا استخدام الصيغ الموضحة في القسم أعلاه.
ومع ذلك، لتطبيق صيغ الانحدار الخطي البسيطة، يجب علينا أولاً حساب متوسط المتغير المستقل ومتوسط المتغير التابع:
![Rendered by QuickLaTeX.com \begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7a7aa6f1f20fa4ff0d61a2ad0dd2ea1f_l3.png)
الآن بعد أن عرفنا متوسطات المتغيرات، نحسب المعامل b 1 للنموذج باستخدام الصيغة المقابلة له:
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c9d90c766487cd7b6924e6b23d2d9c78_l3.png)
وأخيرًا، نحسب المعامل b 0 للنموذج باستخدام الصيغة المقابلة له:
![Rendered by QuickLaTeX.com \begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c72e6b89a75681a88cf751ca39079240_l3.png)
وباختصار، فإن معادلة نموذج الانحدار الخطي البسيط للمشكلة هي:
![]()
يمكنك أدناه رؤية التمثيل الرسومي لبيانات العينة بالإضافة إلى الخط المستقيم لنموذج الانحدار الخطي البسيط:

وأخيرا، بمجرد أن قمنا بحساب معادلة نموذج الانحدار الخطي البسيط، كل ما تبقى هو تفسير النتيجة التي تم الحصول عليها. ولهذا من الضروري حساب معامل تحديد نموذج الانحدار، ويمكنك معرفة كيفية القيام بذلك من خلال البحث عن المقالة المقابلة على موقعنا.
افتراضات الانحدار الخطي البسيط
من أجل إجراء الانحدار الخطي البسيط، يجب استيفاء الافتراضات التالية:
- الاستقلال : يجب أن تكون المخلفات المرصودة مستقلة عن بعضها البعض. إحدى الطرق الشائعة لضمان استقلالية النموذج هي إضافة العشوائية إلى عملية أخذ العينات.
- التجانس : يجب أن يكون هناك تجانس في تباينات البقايا، أي أن تباين البقايا يجب أن يكون ثابتاً.
- الحالة الطبيعية : يجب أن يتم توزيع البقايا بشكل طبيعي، أو بمعنى آخر، يجب أن تتبع التوزيع الطبيعي بمتوسط 0.
- الخطية – يجب أن تكون العلاقة بين المتغير المستقل والمتغير التابع خطية.
حاسبة الانحدار الخطي البسيط
قم بتوصيل عينة من البيانات في الآلة الحاسبة أدناه لتناسب نموذج الانحدار الخطي البسيط بين متغيرين. تحتاج إلى فصل أزواج البيانات، بحيث يوجد في المربع الأول فقط قيم المتغير المستقل X وفي المربع الثاني يوجد فقط قيم المتغير التابع Y.
يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.
الانحدار الخطي البسيط والمتعدد
وأخيرا، سوف نرى ما هو الفرق بين الانحدار الخطي البسيط والانحدار الخطي المتعدد، حيث أنهما نوعان من الانحدارات الخطية المستخدمة بشكل متكرر في الإحصاء.
يتيح الانحدار الخطي المتعدد ربط متغيرين توضيحيين أو أكثر رياضيًا بمتغير الاستجابة. أي أنه في الانحدار الخطي المتعدد، يتم إنشاء نموذج يوجد فيه متغيرين مستقلين على الأقل.
ولذلك، فإن الفرق بين الانحدار الخطي البسيط والانحدار الخطي المتعدد هو عدد المتغيرات المستقلة. في الانحدار الخطي البسيط، يوجد متغير مستقل واحد فقط، بينما في الانحدار الخطي المتعدد، هناك متغيران مستقلان أو أكثر.