كيفية تنفيذ الانحدار الخطي البسيط في إكسيل

الانحدار الخطي البسيط هو أسلوب يمكننا استخدامه لفهم العلاقة بين المتغير التوضيحي x ومتغير الاستجابة y.

يشرح هذا البرنامج التعليمي كيفية إجراء انحدار خطي بسيط في Excel.

مثال: الانحدار الخطي البسيط في Excel

لنفترض أننا نريد أن نفهم العلاقة بين عدد الساعات التي يدرسها الطالب للامتحان والدرجة التي يحصل عليها في الامتحان.

لاستكشاف هذه العلاقة، يمكننا إجراء انحدار خطي بسيط باستخدام ساعات الدراسة كمتغير توضيحي ودرجات الامتحان كمتغير الاستجابة.

أكمل الخطوات التالية في Excel لإجراء انحدار خطي بسيط.

الخطوة 1: أدخل البيانات.

أدخل البيانات التالية لعدد الساعات المدروسة ودرجة الامتحان التي تم الحصول عليها لـ 20 طالباً:

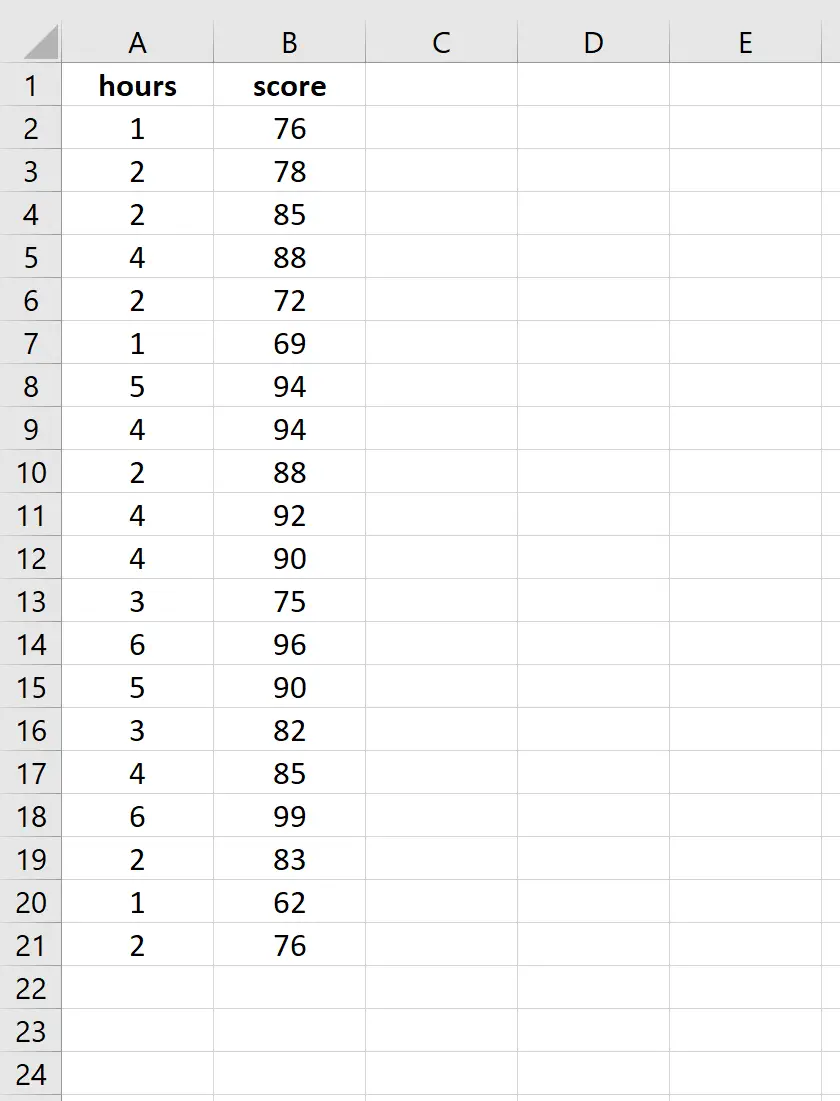
الخطوة 2: تصور البيانات.

قبل إجراء انحدار خطي بسيط، من المفيد إنشاء مخطط مبعثر للبيانات للتأكد من وجود علاقة خطية حقيقية بين ساعات الدراسة ودرجة الامتحان.

قم بتمييز البيانات الموجودة في العمودين A وB. على طول الشريط العلوي لبرنامج Excel، انتقل إلى علامة التبويب “إدراج” . في مجموعة الرسومات ، انقر فوق Insert Scatter (X, Y) وانقر فوق الخيار الأول المسمى Scatter . سيؤدي هذا تلقائيًا إلى إنتاج السحابة النقطية التالية:

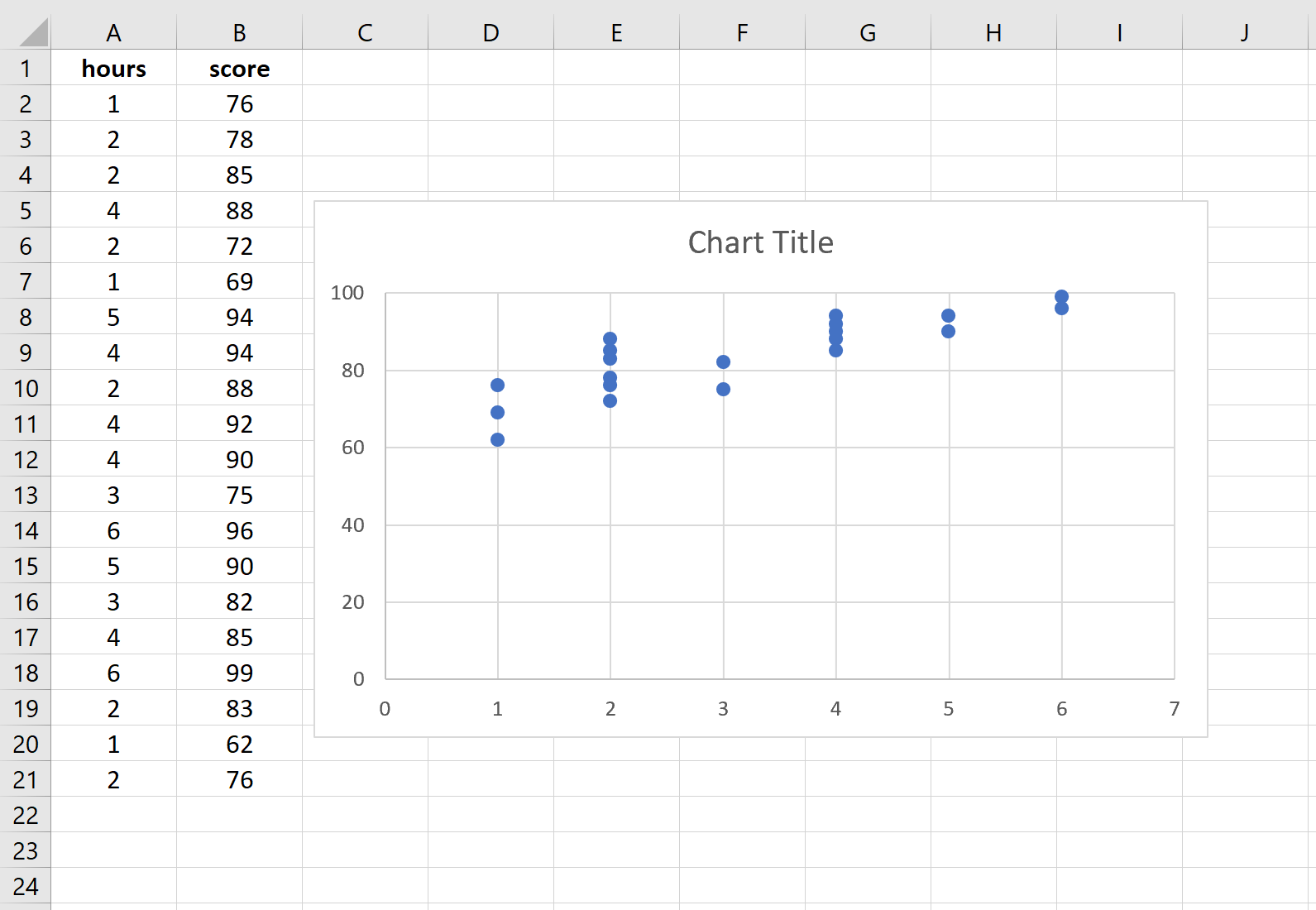
يتم عرض عدد الساعات المدروسة على المحور السيني وتظهر نتائج الامتحانات على المحور الصادي. يمكننا أن نرى أن هناك علاقة خطية بين المتغيرين: المزيد من ساعات الدراسة ترتبط بدرجات أعلى في الامتحانات.

لتحديد العلاقة بين هذين المتغيرين، يمكننا إجراء انحدار خطي بسيط.

الخطوة 3: إجراء الانحدار الخطي البسيط.

في الشريط العلوي لبرنامج Excel، انتقل إلى علامة التبويب “البيانات” وانقر فوق “تحليل البيانات” . إذا لم تشاهد هذا الخيار، فيجب عليك أولاً تثبيت برنامج Analysis ToolPak المجاني .

بمجرد النقر على تحليل البيانات، ستظهر نافذة جديدة. حدد الانحدار وانقر فوق موافق.

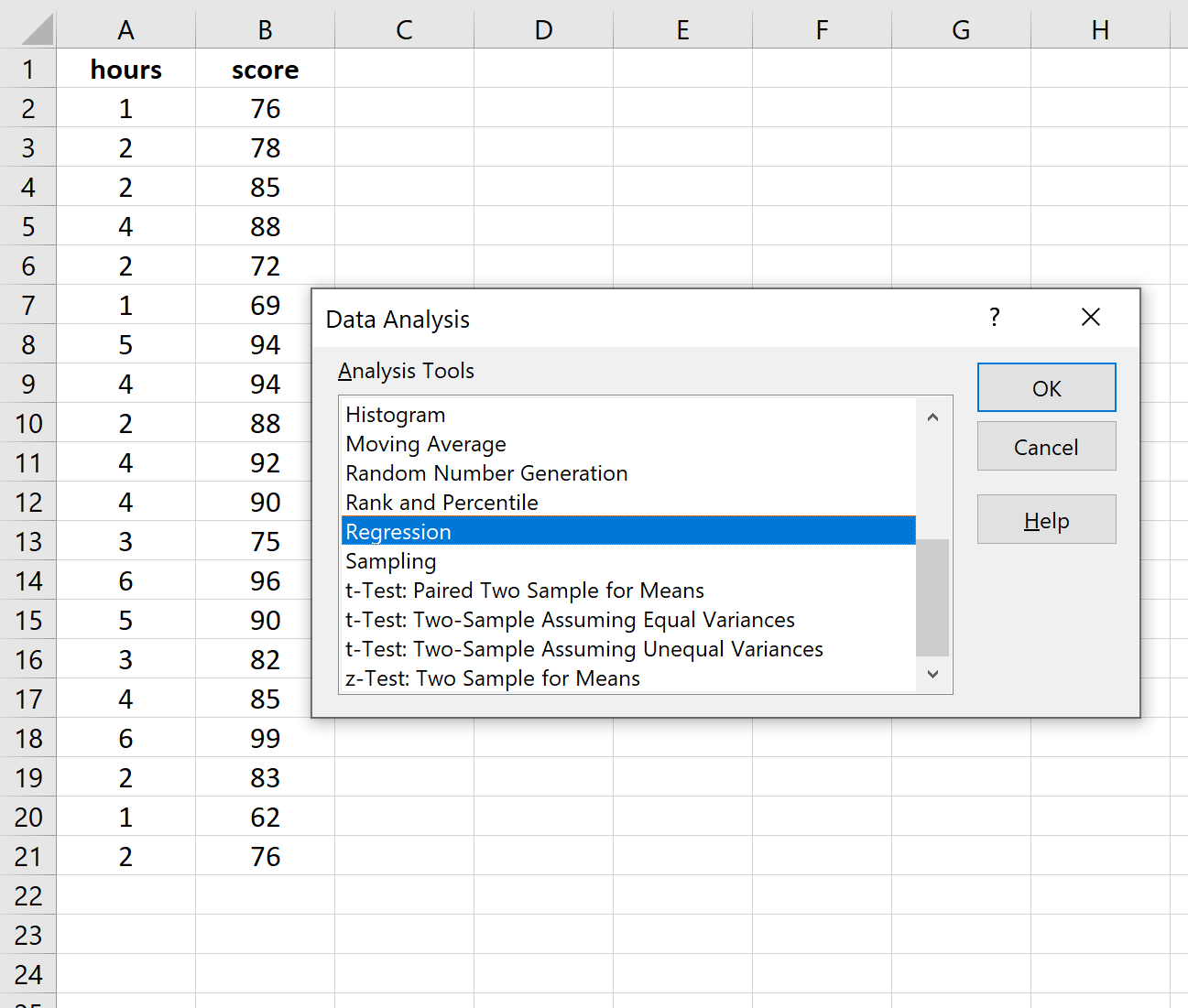
بالنسبة لنطاق الإدخال Y ، املأ مصفوفة القيم لمتغير الاستجابة. بالنسبة لنطاق الإدخال X ، املأ مصفوفة القيم للمتغير التوضيحي.

حدد المربع الموجود بجوار التسميات لإعلام Excel بأننا قمنا بتضمين أسماء المتغيرات في نطاقات الإدخال.

بالنسبة لنطاق الإخراج ، حدد الخلية التي تريد ظهور مخرجات الانحدار فيها.

ثم انقر فوق موافق .

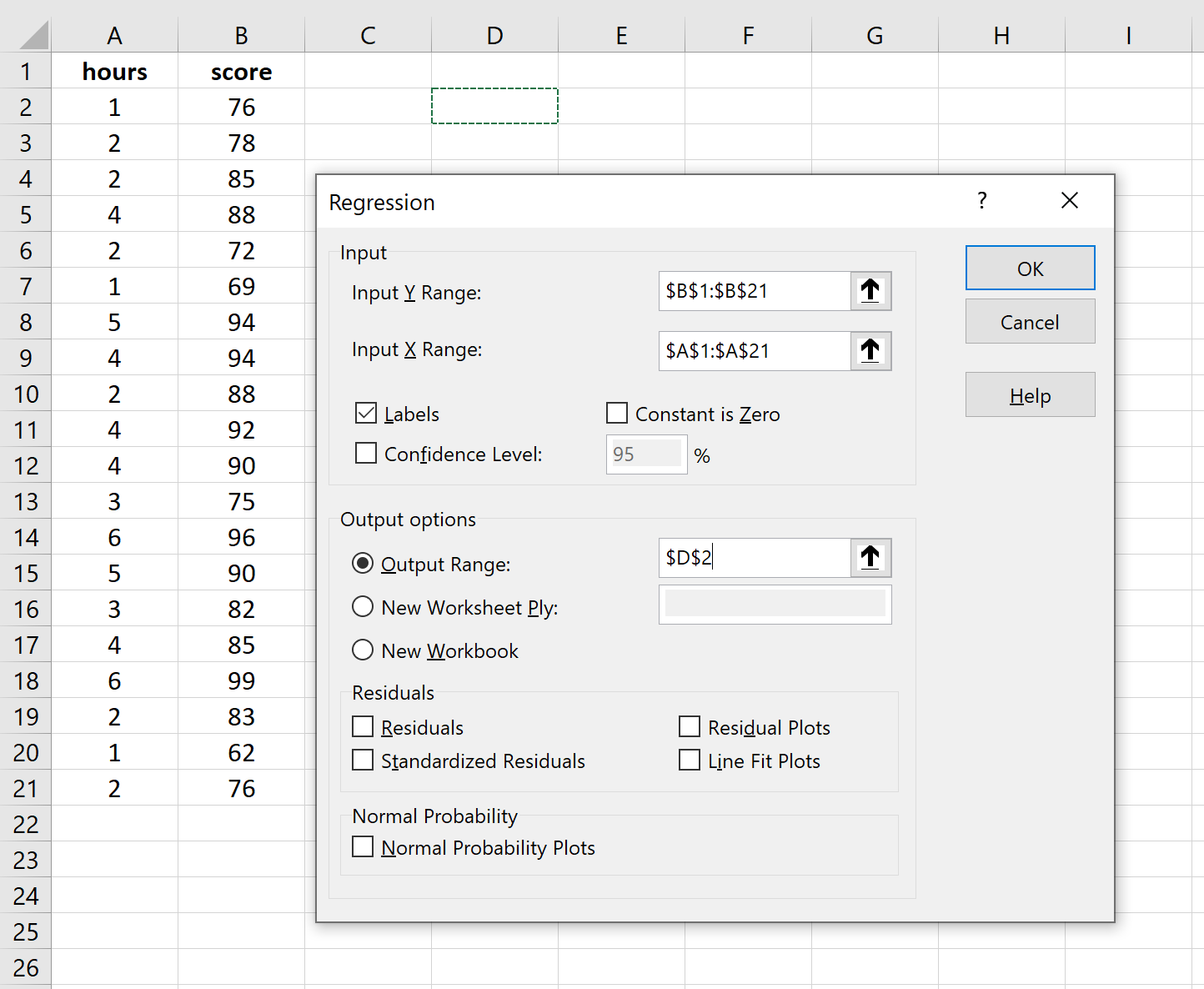
سيظهر الإخراج التالي تلقائيًا:

الخطوة 4: تفسير النتيجة.

فيما يلي كيفية تفسير الأرقام الأكثر صلة بالنتيجة:

ص مربع : 0.7273 . وهذا ما يسمى معامل التحديد. هي نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بالمتغير التوضيحي. في هذا المثال، يتم تفسير 72.73% من التباين في درجات الامتحان بعدد ساعات الدراسة.

الخطأ القياسي: 5.2805 . هذا هو متوسط المسافة بين القيم المرصودة وخط الانحدار. في هذا المثال، تنحرف القيم المرصودة في المتوسط بمقدار 5.2805 وحدة عن خط الانحدار.

ف : 47.9952 . هذه هي إحصائية F الإجمالية لنموذج الانحدار، والتي يتم حسابها على أنها MS انحدار/MS المتبقية.

المعنى ف : 0.0000 . هذه هي القيمة p المرتبطة بإحصائيات F الإجمالية. يخبرنا هذا ما إذا كان نموذج الانحدار ذو دلالة إحصائية أم لا. وبعبارة أخرى، فإنه يخبرنا ما إذا كان المتغير التوضيحي له ارتباط ذو دلالة إحصائية مع متغير الاستجابة. وفي هذه الحالة تكون القيمة p أقل من 0.05، مما يشير إلى وجود علاقة ذات دلالة إحصائية بين الساعات المدروسة والدرجة التي تم الحصول عليها في الامتحان.

المعاملات: تعطينا المعاملات الأرقام اللازمة لكتابة معادلة الانحدار المقدرة. في هذا المثال، معادلة الانحدار المقدرة هي:

درجة الامتحان = 67.16 + 5.2503*(ساعات)

نفسر معامل الساعات على أنه مقابل كل ساعة إضافية تتم دراستها، يجب أن تزيد درجة الامتحان بمقدار 5.2503 في المتوسط. نفسر معامل التقاطع على أنه يعني أن درجة الامتحان المتوقعة للطالب الذي يدرس صفر ساعة هي 67.16 .

يمكننا استخدام معادلة الانحدار المقدرة هذه لحساب درجة الامتحان المتوقعة للطالب، بناءً على عدد ساعات الدراسة.

على سبيل المثال، الطالب الذي يدرس لمدة ثلاث ساعات يجب أن يحقق درجة الامتحان 82.91 :

درجة الامتحان = 67.16 + 5.2503*(3) = 82.91

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في Excel:

كيفية إنشاء مؤامرة المتبقية في إكسيل
كيفية بناء فترة التنبؤ في إكسيل
كيفية إنشاء مؤامرة QQ في إكسيل