مقدمة في الانحدار اللوجستي

عندما نريد أن نفهم العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة المستمرة، فإننا غالبًا ما نستخدم الانحدار الخطي .

ومع ذلك، عندما يكون متغير الاستجابة قاطعًا، يمكننا استخدام الانحدار اللوجستي .

الانحدار اللوجستي هو نوع من خوارزمية التصنيف لأنه يحاول “تصنيف” الملاحظات في مجموعة البيانات إلى فئات متميزة.

فيما يلي بعض الأمثلة على استخدام الانحدار اللوجستي:

• نريد استخدام درجة الائتمان والرصيد البنكي للتنبؤ بما إذا كان عميل معين سيتخلف عن سداد القرض. (متغير الاستجابة = “افتراضي” أو “لا يوجد افتراضي”)
• نريد استخدام متوسط الكرات المرتدة لكل مباراة ومتوسط النقاط لكل لعبة للتنبؤ بما إذا كان لاعب كرة سلة معين سيتم تجنيده في الدوري الاميركي للمحترفين أم لا (متغير الاستجابة = “تمت صياغته” أو “غير تمت صياغته”).
• نريد استخدام اللقطات المربعة وعدد الحمامات للتنبؤ بما إذا كان سيتم إدراج منزل في مدينة معينة بسعر بيع قدره 200000 دولار أو أكثر أم لا. (متغير الاستجابة = “نعم” أو “لا”)

لاحظ أن متغير الاستجابة في كل من هذه الأمثلة يمكن أن يأخذ قيمة واحدة فقط من قيمتين. قارن ذلك بالانحدار الخطي الذي يأخذ فيه متغير الاستجابة قيمة مستمرة.

معادلة الانحدار اللوجستي

يستخدم الانحدار اللوجستي طريقة تعرف بتقدير الاحتمالية القصوى (لن تتم مناقشة التفاصيل هنا) للعثور على معادلة بالشكل التالي:

سجل[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

ذهب:

• X _j : ^{المتغير} التنبئي j
• β _j : تقدير معامل المتغير التنبئي ^j

تتنبأ الصيغة الموجودة على الجانب الأيمن من المعادلة باحتمالات السجل التي يأخذ فيها متغير الاستجابة القيمة 1.

لذلك، عندما نلائم نموذج الانحدار اللوجستي، يمكننا استخدام المعادلة التالية لحساب احتمال أن تأخذ ملاحظة معينة القيمة 1:

ص(X) = ه ^{β ₀ + β _{1 X 1 + β 2 X 2 + … + β ص}}

نستخدم بعد ذلك عتبة احتمالية معينة لتصنيف الملاحظة على أنها 1 أو 0.

على سبيل المثال، يمكننا القول أن الملاحظات ذات الاحتمالية الأكبر من أو تساوي 0.5 سيتم تصنيفها على أنها “1” وسيتم تصنيف جميع الملاحظات الأخرى على أنها “0”.

كيفية تفسير نتيجة الانحدار اللوجستي

لنفترض أننا نستخدم نموذج الانحدار اللوجستي للتنبؤ بما إذا كان لاعب كرة سلة معين سيتم تجنيده في الدوري الاميركي للمحترفين أم لا بناءً على متوسط كراته المرتدة في كل مباراة ومتوسط نقاطه في كل مباراة.

هذه هي نتيجة نموذج الانحدار اللوجستي:

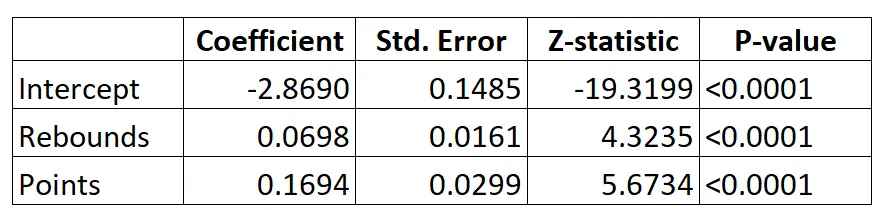
باستخدام المعاملات، يمكننا حساب احتمالية انضمام لاعب معين إلى الدوري الاميركي للمحترفين بناءً على متوسط الكرات المرتدة والنقاط لكل مباراة باستخدام الصيغة التالية:

P(مسودة) = e ^{-2.8690 + 0.0698*(rebs) + 0.1694*(نقاط)} / (1+e ^{-2.8690 + 0.0698*(rebs) + 0.1694*(نقاط)))}

على سبيل المثال، لنفترض أن لاعبًا معينًا يبلغ متوسطه 8 كرات مرتدة في المباراة الواحدة و15 نقطة في المباراة الواحدة. وفقًا للنموذج، فإن احتمال تجنيد هذا اللاعب في الدوري الاميركي للمحترفين هو 0.557 .

P(مكتوبة) = ه ^{-2.8690 + 0.0698*(8) + 0.1694*(15)} / (1+ه ^{-2.8690 + 0.0698*(8) + 0.1694*(15 )} ) = 0.557

وبما أن هذا الاحتمال أكبر من 0.5، فإننا نتوقع أن يتم تجنيد هذا اللاعب.

قارن ذلك باللاعب الذي يبلغ متوسطه 3 متابعات و7 نقاط فقط في المباراة الواحدة. احتمال تجنيد هذا اللاعب في الدوري الاميركي للمحترفين هو 0.186 .

P(مكتوبة) = ه ^{-2.8690 + 0.0698*(3) + 0.1694*(7)} / (1+ه ^{-2.8690 + 0.0698*(3) + 0.1694*(7 )} ) = 0.186

وبما أن هذا الاحتمال أقل من 0.5، فإننا نتوقع عدم تجنيد هذا اللاعب.

افتراضات الانحدار اللوجستي

يستخدم الانحدار اللوجستي الافتراضات التالية:

1. متغير الاستجابة ثنائي. من المفترض أن متغير الاستجابة يمكن أن يأخذ نتيجتين محتملتين فقط.

2. الملاحظات مستقلة. من المفترض أن الملاحظات في مجموعة البيانات مستقلة عن بعضها البعض. أي أن الملاحظات لا ينبغي أن تأتي من قياسات متكررة لنفس الفرد أو أن تكون مرتبطة ببعضها البعض بأي شكل من الأشكال.

3. لا توجد علاقة خطية جدية بين المتغيرات المتنبئة . من المفترض أن أيا من متغيرات التوقع لا ترتبط ارتباطا وثيقا مع بعضها البعض.

4. لا توجد قيم متطرفة. من المفترض أنه لا توجد قيم متطرفة أو ملاحظات مؤثرة في مجموعة البيانات.

5. توجد علاقة خطية بين متغيرات التوقع ولوجيتم متغير الاستجابة . ويمكن اختبار هذه الفرضية باستخدام اختبار Box-Tidwell.

6. حجم العينة كبير بما فيه الكفاية. عادةً، يجب أن يكون لديك ما لا يقل عن 10 حالات مع النتيجة الأقل تكرارًا لكل متغير توضيحي. على سبيل المثال، إذا كان لديك 3 متغيرات توضيحية وكان الاحتمال المتوقع للنتيجة الأقل تكرارًا هو 0.20، فيجب أن يكون حجم العينة لديك على الأقل (10*3) / 0.20 = 150.

راجع هذه المقالة للحصول على شرح مفصل لكيفية التحقق من هذه الافتراضات.