كيفية تنفيذ الانحدار اللوجستي في بايثون (خطوة بخطوة)

الانحدار اللوجستي هو طريقة يمكننا استخدامها لتناسب نموذج الانحدار عندما يكون متغير الاستجابة ثنائيًا.

يستخدم الانحدار اللوجستي طريقة تعرف بتقدير الاحتمالية القصوى للعثور على معادلة بالشكل التالي:

سجل[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

ذهب:

• X _j : ^{المتغير} التنبئي j
• β _j : تقدير معامل المتغير التنبئي ^j

تتنبأ الصيغة الموجودة على الجانب الأيمن من المعادلة باحتمالات السجل التي يأخذ فيها متغير الاستجابة القيمة 1.

لذلك، عندما نلائم نموذج الانحدار اللوجستي، يمكننا استخدام المعادلة التالية لحساب احتمال أن تأخذ ملاحظة معينة القيمة 1:

ص(X) = ه ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} ص

نستخدم بعد ذلك عتبة احتمالية معينة لتصنيف الملاحظة على أنها 1 أو 0.

على سبيل المثال، يمكننا القول أن الملاحظات ذات الاحتمالية الأكبر من أو تساوي 0.5 سيتم تصنيفها على أنها “1” وسيتم تصنيف جميع الملاحظات الأخرى على أنها “0”.

يوفر هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية إجراء الانحدار اللوجستي في R.

الخطوة 1: استيراد الحزم اللازمة

أولاً، سنقوم باستيراد الحزم اللازمة لإجراء الانحدار اللوجستي في بايثون:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

الخطوة 2: تحميل البيانات

في هذا المثال، سوف نستخدم مجموعة البيانات الافتراضية من كتاب مقدمة إلى التعلم الإحصائي . يمكننا استخدام الكود التالي لتحميل وعرض ملخص لمجموعة البيانات:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/- Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

تحتوي مجموعة البيانات هذه على المعلومات التالية عن 10000 فرد:

• الافتراضي: يشير إلى ما إذا كان الفرد قد تخلف أم لا.
• الطالب: يشير إلى ما إذا كان الفرد طالبًا أم لا.
• الرصيد: متوسط الرصيد الذي يحمله الفرد.
• الدخل: دخل الفرد.

سوف نستخدم حالة الطالب، والرصيد البنكي، والدخل لبناء نموذج الانحدار اللوجستي الذي يتنبأ باحتمالية تخلف فرد معين عن السداد.

الخطوة 3: إنشاء عينات التدريب والاختبار

بعد ذلك، سنقوم بتقسيم مجموعة البيانات إلى مجموعة تدريب لتدريب النموذج عليها ومجموعة اختبار لاختبار النموذج عليها.

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

الخطوة 4: ملاءمة نموذج الانحدار اللوجستي

بعد ذلك، سنستخدم الدالة LogisticRegression() ‎ لملاءمة نموذج الانحدار اللوجستي لمجموعة البيانات:

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

الخطوة 5: تشخيص النماذج

بمجرد تركيب نموذج الانحدار، يمكننا بعد ذلك تحليل أداء نموذجنا في مجموعة بيانات الاختبار.

أولاً، سنقوم بإنشاء مصفوفة الارتباك للنموذج:

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

من مصفوفة الارتباك يمكننا أن نرى أن:

• #التوقعات الإيجابية الحقيقية: 2886
• #التوقعات السلبية الحقيقية: 0
• #التوقعات الإيجابية الكاذبة: 113
• #التوقعات السلبية الكاذبة: 1

يمكننا أيضًا الحصول على نموذج الدقة الذي يخبرنا بنسبة تنبؤات التصحيح التي أجراها النموذج:

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

يخبرنا هذا أن النموذج قام بالتنبؤ الصحيح حول ما إذا كان الفرد سيتخلف عن السداد بنسبة 96.2% من الوقت أم لا.

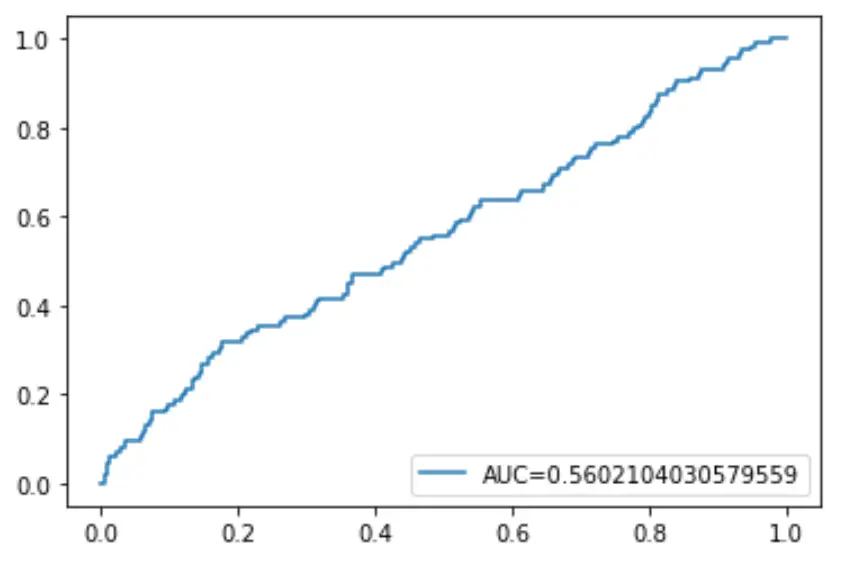
أخيرًا، يمكننا رسم منحنى خاصية تشغيل المستقبل (ROC) الذي يعرض النسبة المئوية للإيجابيات الحقيقية التي تنبأ بها النموذج عندما يتم تخفيض عتبة احتمال التنبؤ من 1 إلى 0.

كلما ارتفعت المساحة تحت المنحنى (AUC)، زادت دقة نموذجنا في التنبؤ بالنتائج:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()