الانحراف المعياري النسبي

تشرح هذه المقالة كيفية حساب الانحراف المعياري النسبي. سوف تكتشف ما هو الانحراف المعياري النسبي، وما هي صيغته، بالإضافة إلى تمرين تم حله خطوة بخطوة.

ما هو الانحراف المعياري النسبي؟

الانحراف المعياري النسبي هو مقياس إحصائي يشير إلى تشتت مجموعة البيانات بالنسبة لمتوسطها. يتم حساب الانحراف المعياري النسبي عن طريق قسمة الانحراف المعياري للبيانات على متوسطها.

يتم التعبير عن الانحراف المعياري النسبي كنسبة مئوية وستكون قيمته دائمًا موجبة.

يتم استخدام تفسير الانحراف المعياري النسبي لإظهار تشتت عينة البيانات. كلما زادت قيمة الانحراف المعياري النسبي، زادت تشتت البيانات. وكلما كان الانحراف المعياري النسبي أصغر، كلما كانت البيانات أقرب إلى وسطها.

بشكل عام، يتم استخدام اختصار RSD كرمز للانحراف المعياري النسبي .

صيغة الانحراف المعياري النسبي

الانحراف المعياري النسبي يساوي الانحراف المعياري مقسومًا على الوسط مضروبًا في 100. لذلك، لحساب الانحراف المعياري النسبي، يجب عليك أولاً تحديد الانحراف المعياري والوسط الحسابي، ثم قسمة القياسين الإحصائيين وأخيرًا الضرب في 100.

وبعبارة أخرى، فإن صيغة الانحراف المعياري النسبي هي:

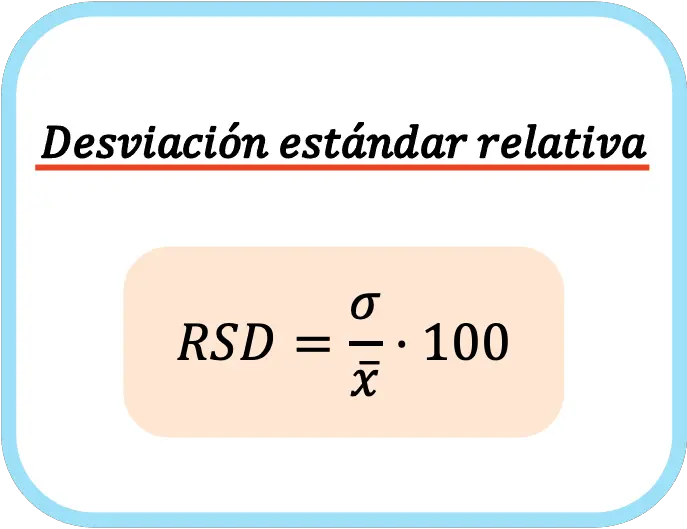
عند حساب الانحراف المعياري النسبي، يتم ضربه في مائة للتعبير عن القيمة كنسبة مئوية.

مثال لحساب الانحراف المعياري النسبي

بعد الاطلاع على تعريف الانحراف المعياري النسبي وصيغته، يمكنك أدناه رؤية مثال ملموس لكيفية حساب الانحراف المعياري النسبي.

• احسب الانحراف المعياري النسبي لمجموعة البيانات الإحصائية التالية:
  4, 1, 3, 9, 12, 2, 5, 8, 3, 6

أولاً، نحتاج إلى إيجاد الانحراف المعياري للبيانات:

ثانياً، نحسب الوسط الحسابي للبيانات:

بمجرد أن نعرف الانحراف المعياري والوسط الحسابي لسلسلة البيانات، نستخدم صيغة الانحراف المعياري النسبي.

وأخيرًا، نستبدل القيم المحسوبة في الصيغة ونحسب الانحراف المعياري النسبي: