كيفية تقدير الانحراف المعياري لأي رسم بياني

يوفر الرسم البياني طريقة مفيدة لتصور توزيع القيم في مجموعة البيانات.

يعرض المحور السيني للرسم البياني مجموعات من قيم البيانات ويخبرنا المحور الصادي بعدد الملاحظات في مجموعة البيانات الموجودة في كل مجموعة.

نظرًا لأن الرسم البياني يضع الملاحظات في صناديق، فمن غير الممكن حساب الانحراف المعياري الدقيق لمجموعة البيانات التي يمثلها الرسم البياني، ولكن من الممكن تقدير الانحراف المعياري.

يوضح المثال التالي كيفية القيام بذلك.

ذات صلة: كيفية تقدير المتوسط والوسيط لأي رسم بياني

كيفية تقدير الانحراف المعياري للرسم البياني

من أجل تقدير الانحراف المعياري للرسم البياني، يجب عليك أولا تقدير المتوسط.

يمكننا استخدام الصيغة التالية لتقدير المتوسط:

المتوسط: Σm _i n _i / N

ذهب:

• m _i : منتصف ^{الصندوق} i
• n _i : تردد ^{الصندوق} i
• N: إجمالي حجم العينة

على سبيل المثال، لنفترض أن لدينا الرسم البياني التالي:

فيما يلي كيفية تقدير متوسط قيمة هذا الرسم البياني:

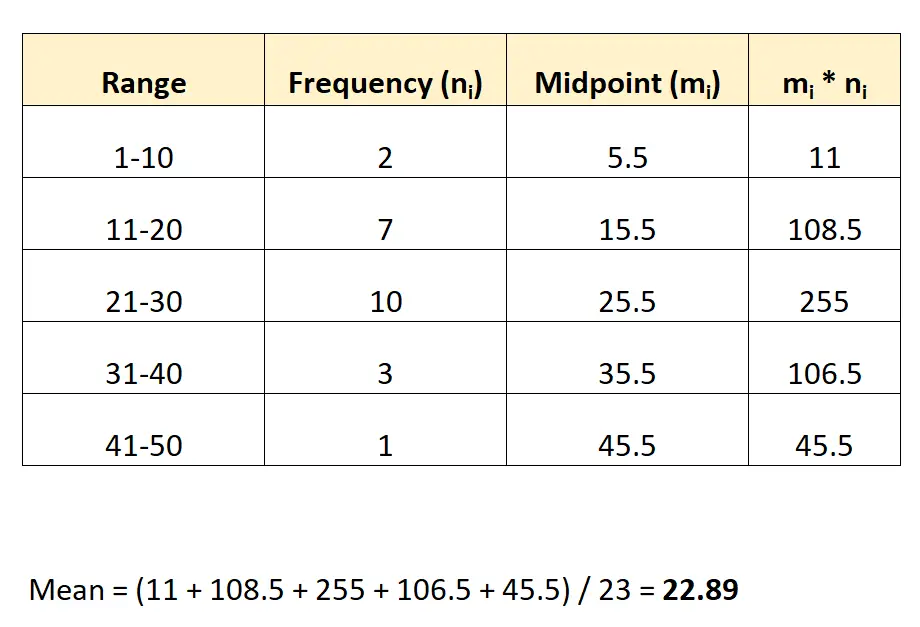
نحن نقدر المتوسط عند 22.89 .

ملحوظة: يمكن إيجاد نقطة المنتصف لكل مجموعة عن طريق أخذ متوسط القيم الدنيا والعليا للنطاق. على سبيل المثال، يتم حساب نقطة منتصف المجموعة الأولى على النحو التالي: (1+10) / 2 = 5.5.

الآن بعد أن أصبح لدينا تقدير للمتوسط، يمكننا استخدام الصيغة التالية لتقدير الانحراف المعياري:

الانحراف المعياري: √ Σn _i (m _i -μ) ² / (N-1)

ذهب:

• n _i : تردد ^{الصندوق} i
• m _i : منتصف ^{الصندوق} i
• م : المتوسط
• N: إجمالي حجم العينة

إليك كيفية تطبيق هذه الصيغة على مجموعة البيانات الخاصة بنا:

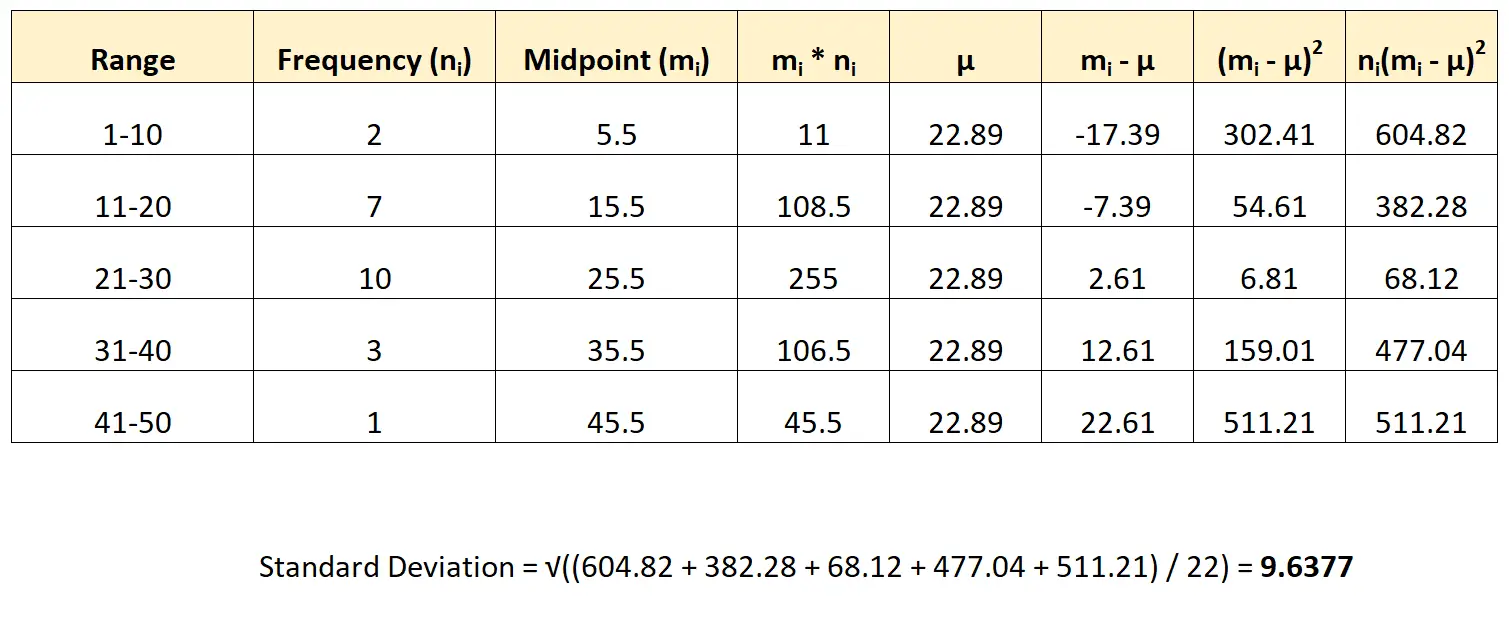نحن نقدر الانحراف المعياري لمجموعة البيانات ليكون 9.6377 .

على الرغم من أنه ليس مضمونًا تطابق الانحراف المعياري لمجموعة البيانات تمامًا (نظرًا لأننا لا نعرف قيم البيانات الأولية لمجموعة البيانات)، إلا أنه يمثل أفضل تقدير لدينا للانحراف المعياري.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى المتعلقة بالبيانات المجمعة في مجموعات:

كيفية العثور على تباين البيانات المجمعة
كيفية العثور على متوسط البيانات المجمعة
كيفية العثور على وضع البيانات المجمعة