فهم الخطأ القياسي لمنحدر الانحدار

الخطأ المعياري لمنحدر الانحدار هو وسيلة لقياس “عدم اليقين” في تقدير منحدر الانحدار.

يتم حسابه على النحو التالي:

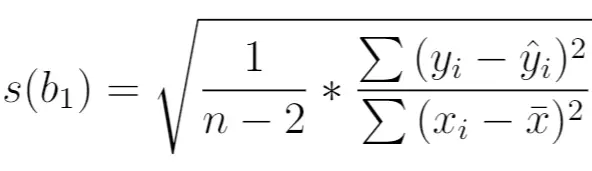
ذهب:

• n : حجم العينة الإجمالي
• y _i : القيمة الحقيقية لمتغير الاستجابة
• ŷ _i : القيمة المتوقعة لمتغير الاستجابة
• x _i : القيمة الحقيقية للمتغير التنبؤي
• x̄ : متوسط قيمة المتغير التنبؤي

كلما كان الخطأ المعياري أصغر، قل التباين حول تقدير المعامل لمنحدر الانحدار.

سيتم عرض الخطأ القياسي لمنحدر الانحدار في عمود “الخطأ القياسي” في مخرجات الانحدار لمعظم البرامج الإحصائية:

توضح الأمثلة التالية كيفية تفسير الخطأ القياسي لمنحدر الانحدار في سيناريوهين مختلفين.

المثال 1: تفسير خطأ قياسي صغير لمنحدر الانحدار

لنفترض أن الأستاذ يريد أن يفهم العلاقة بين عدد الساعات المدروسة ودرجة الاختبار النهائي للطلاب في فصله.

يقوم بجمع بيانات لـ 25 طالبًا وإنشاء مخطط التشتت التالي:

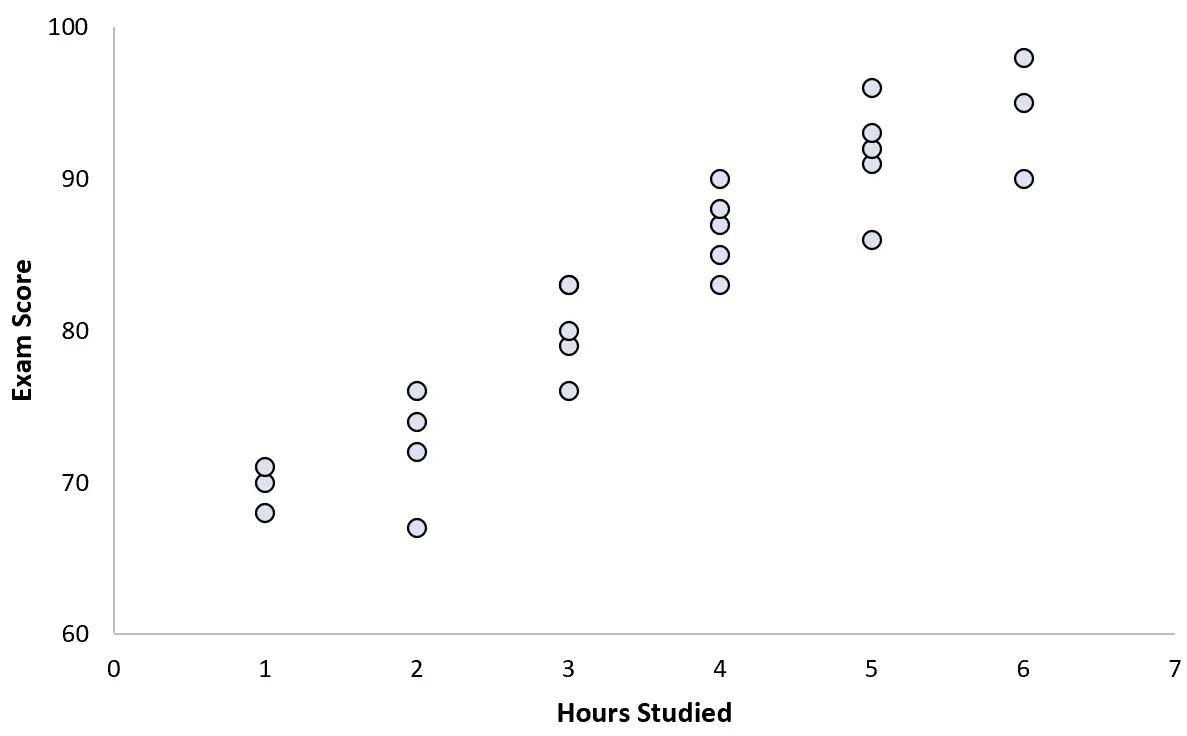
هناك ارتباط إيجابي واضح بين المتغيرين. ومع زيادة عدد ساعات الدراسة، تزداد درجة الامتحان بمعدل يمكن التنبؤ به إلى حد ما.

ثم قام بعد ذلك بتركيب نموذج الانحدار الخطي البسيط باستخدام ساعات الدراسة كمتغير متوقع ودرجة الامتحان النهائي كمتغير الاستجابة.

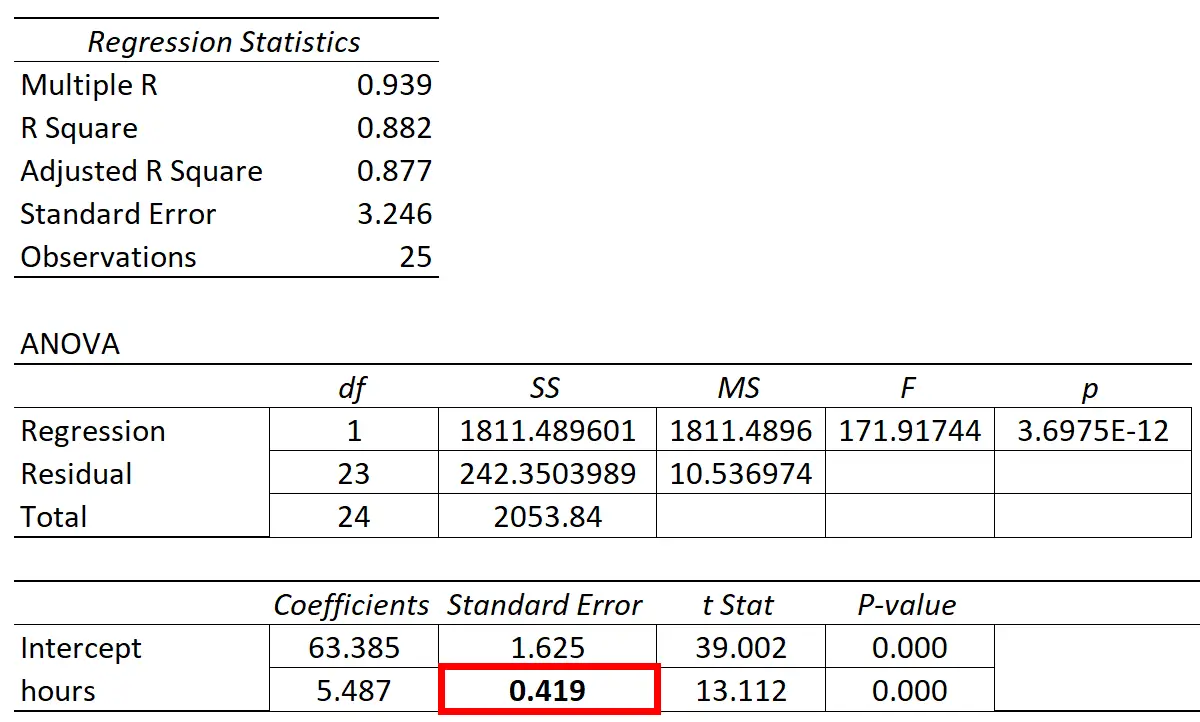
ويبين الجدول التالي نتائج الانحدار:

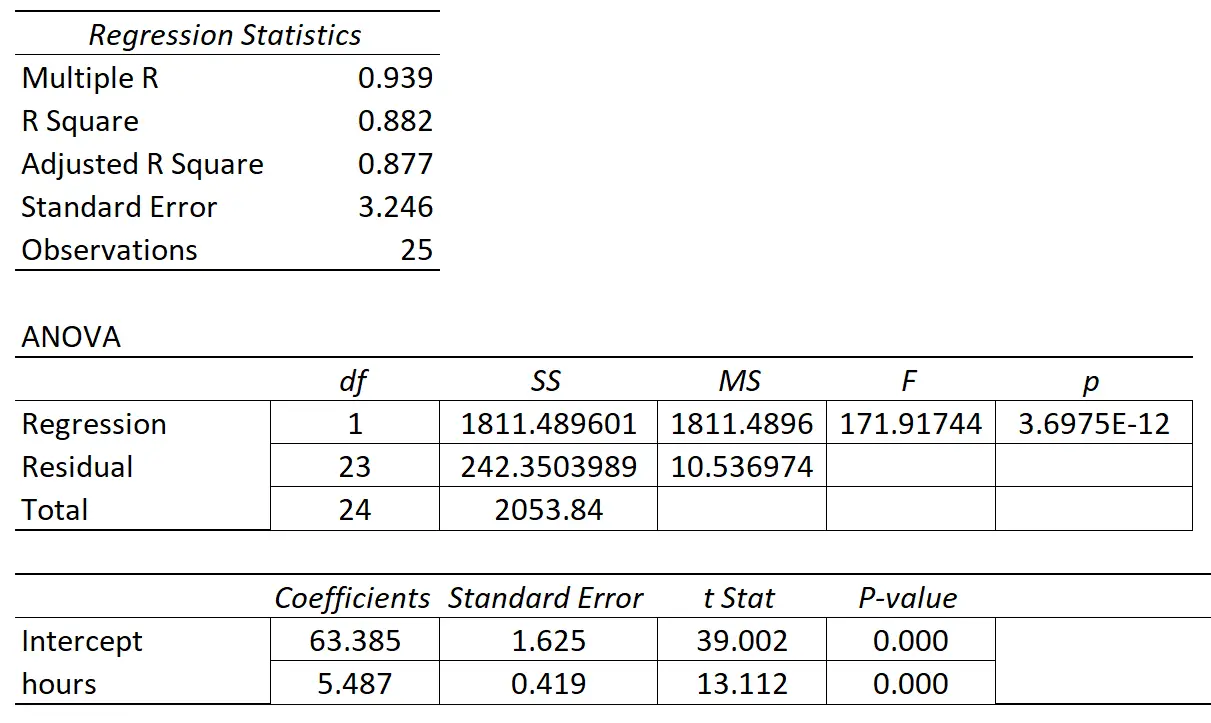
– أن معامل المتغير المتنبأ به “ساعات الدراسة” هو 5.487. وهذا يخبرنا أن كل ساعة إضافية تتم دراستها ترتبط بمتوسط زيادة قدرها 5,487 في درجة الامتحان.

الخطأ المعياري هو 0.419 ، وهو ما يمثل مقياسًا للتباين حول هذا التقدير لمنحدر الانحدار.

يمكننا استخدام هذه القيمة لحساب إحصائية t للمتغير المتنبئ “ساعات الدراسة”:

• t الإحصائية = تقدير المعامل / الخطأ المعياري
• إحصائية t = 5.487 / 0.419
• إحصائيات تي = 13.112

القيمة p التي تتوافق مع إحصائية الاختبار هذه هي 0.000، مما يشير إلى أن “ساعات الدراسة” لها علاقة ذات دلالة إحصائية بدرجة الاختبار النهائي.

ونظرًا لأن الخطأ المعياري لمنحدر الانحدار كان صغيرًا مقارنة بتقدير المعامل لمنحدر الانحدار، فإن متغير التوقع كان ذا دلالة إحصائية.

المثال 2: تفسير خطأ قياسي كبير لمنحدر الانحدار

لنفترض أن أستاذًا آخر يريد فهم العلاقة بين عدد الساعات المدروسة ودرجة الاختبار النهائي للطلاب في فصله.

قامت بجمع بيانات لـ 25 طالبًا وإنشاء مخطط التشتت التالي:

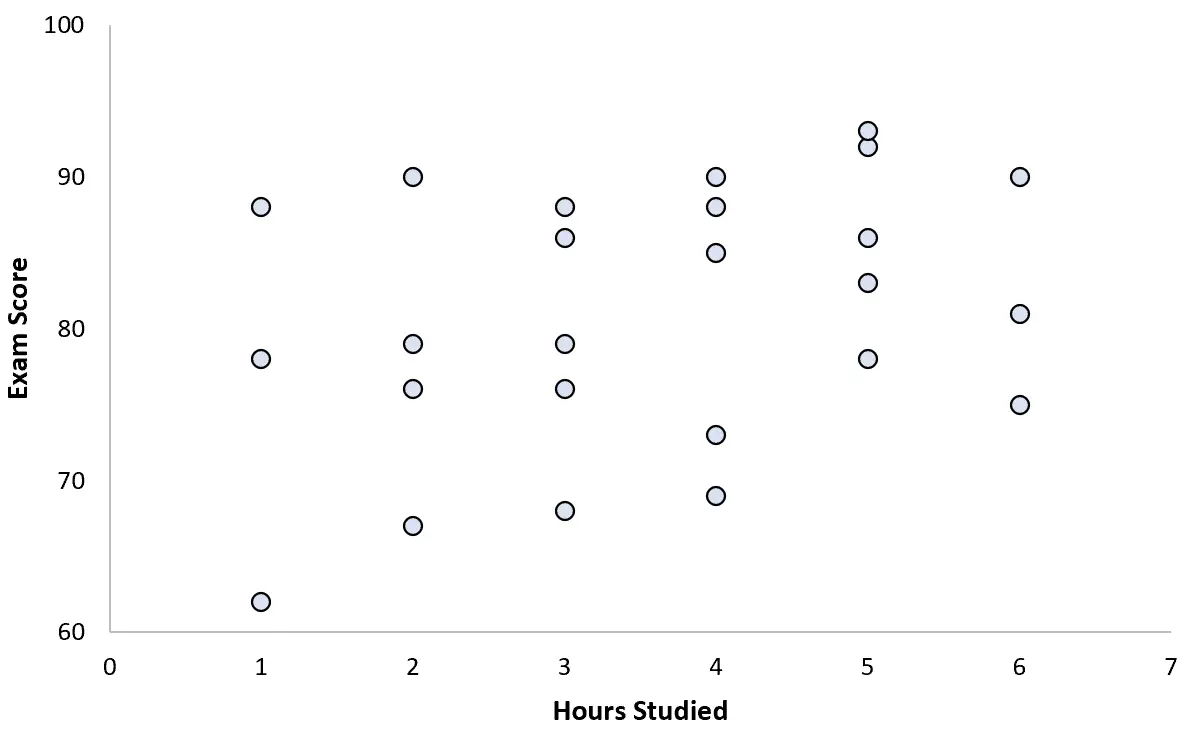
ويبدو أن هناك علاقة إيجابية طفيفة بين المتغيرين. ومع زيادة عدد ساعات الدراسة، تزداد درجة الامتحان بشكل عام، ولكن ليس بمعدل يمكن التنبؤ به.

افترض أن الأستاذ بعد ذلك يناسب نموذج الانحدار الخطي البسيط باستخدام ساعات الدراسة كمتغير متوقع ودرجة الاختبار النهائي كمتغير الاستجابة.

ويبين الجدول التالي نتائج الانحدار:

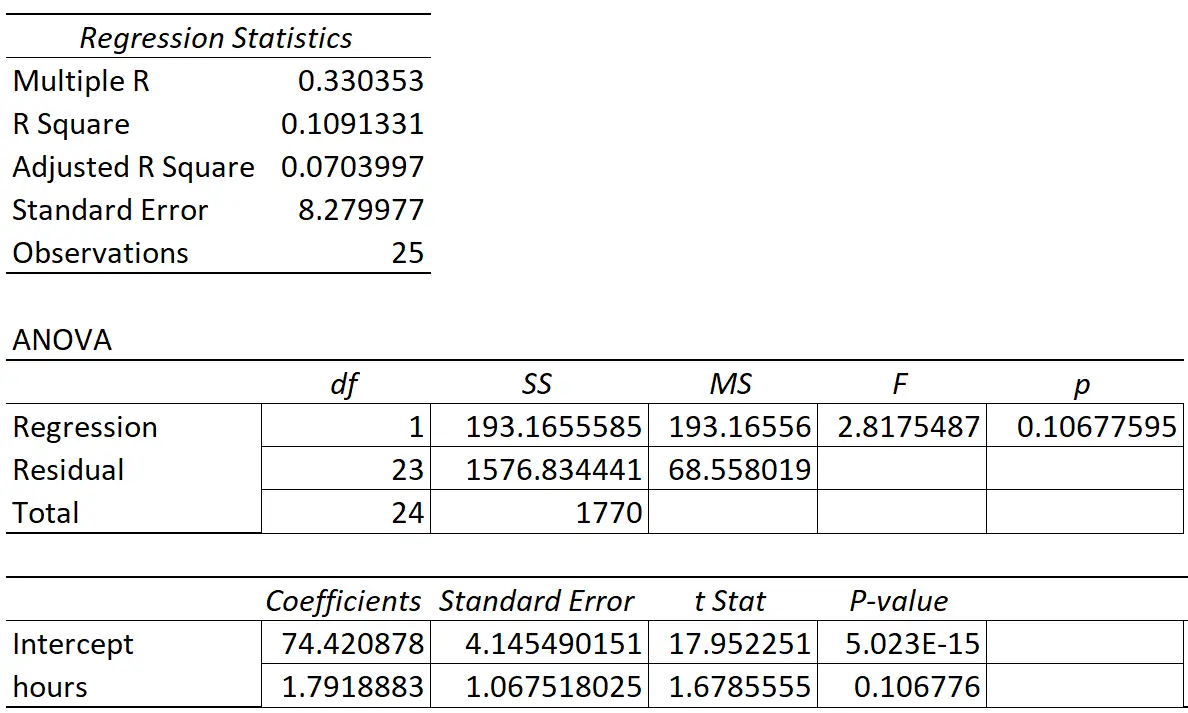
ومعامل المتغير المتنبأ به “ساعات الدراسة” هو 1.7919. وهذا يخبرنا أن كل ساعة إضافية تتم دراستها ترتبط بمتوسط زيادة قدرها 1.7919 في درجة الامتحان.

الخطأ المعياري هو 1.0675 ، وهو مقياس للتباين حول هذا التقدير لمنحدر الانحدار.

يمكننا استخدام هذه القيمة لحساب إحصائية t للمتغير المتنبئ “ساعات الدراسة”:

• t الإحصائية = تقدير المعامل / الخطأ المعياري
• إحصائيات t = 1.7919 / 1.0675
• إحصاء تي = 1.678

القيمة p التي تتوافق مع إحصائيات الاختبار هذه هي 0.107. وبما أن هذه القيمة الاحتمالية لا تقل عن 0.05، فهذا يشير إلى أن “ساعات الدراسة” ليس لها علاقة ذات دلالة إحصائية بدرجة الامتحان النهائي.

ونظرًا لأن الخطأ المعياري لمنحدر الانحدار كان كبيرًا بالنسبة إلى تقدير المعامل لمنحدر الانحدار، فإن متغير التوقع لم يكن ذو دلالة إحصائية.

مصادر إضافية

مقدمة إلى الانحدار الخطي البسيط
مقدمة في الانحدار الخطي المتعدد
كيفية قراءة وتفسير جدول الانحدار