الربعيات
في هذه المقالة نوضح ما هي الربعيات. ستجد تعريف كل ربع وكيفية حسابه والعديد من الأمثلة الملموسة. نعرض لك أيضًا كيفية حساب الشرائح الربعية للبيانات المجمعة. بالإضافة إلى ذلك، سوف تكون قادرًا على حساب الأرباع الربعية لأي مجموعة بيانات باستخدام الآلة الحاسبة عبر الإنترنت.
ما هي الأرباع؟
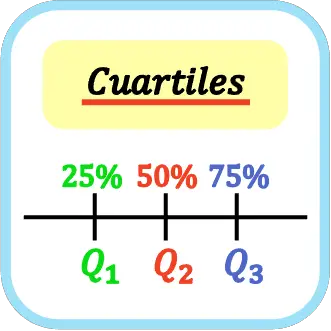
في الإحصاء، الربعيات هي القيم الثلاث التي تقسم مجموعة من البيانات المرتبة إلى أربعة أجزاء متساوية. وبالتالي، تمثل الشرائح الربعية الأولى والثانية والثالثة على التوالي 25% و50% و75% من جميع البيانات الإحصائية.
يتم تمثيل الربيعيات بحرف كبير Q ومؤشر الربعي، وبالتالي فإن الربع الأول هو Q 1 ، والربيع الثاني هو Q 2 ، والربيع الثالث هو Q 3 .
👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب الأرباع الربعية لأي مجموعة بيانات.
تجدر الإشارة إلى أن الربعيات هي مقياس للوضع غير المركزي بنفس طريقة الخماسيات والعشريات والنسب المئوية. يمكنك التحقق من كل نوع من هذه الأنواع الكمية على صفحة الويب هذه.
الربع الأول
الربع الأول ، ويسمى أيضًا الربع 1، هو القيمة الأكبر من 25% من البيانات الإحصائية في العينة. بمعنى آخر، يمثل الربع الأول أكثر من 25% من البيانات المرصودة.
يتم التعبير عن الربع الأول بالرمز Q 1 ويستخدم للدلالة على أصغر قيم البيانات في العينة.
الربع الثاني
الربع الثاني ، ويسمى أيضًا الربع 2، هو القيمة الأكبر من 50% من البيانات الإحصائية في العينة. ولذلك، فإن الربع الثاني يفصل مجموعة البيانات إلى نصفين ويتزامن مع الوسيط والعشيري الخامس.
رمز الربع الثاني هو Q2 .
الربع الثالث
الربع الثالث ، ويسمى أيضًا الربع الثالث، هو القيمة التي تتجاوز 75% من البيانات الإحصائية في العينة. بمعنى آخر، يمثل الربع الثالث أكثر من 75% من البيانات المجمعة.
يتم التعبير عن الربع الثالث بالرمز Q 3 ويمثل أكبر القيم في العينة.
كيفية حساب الربعيات
لحساب موضع الربيعيات في مجموعة بيانات إحصائية، يجب عليك ضرب عدد الربيعيات في مجموع إجمالي عدد البيانات زائد واحد وتقسيم النتيجة على أربعة.
وبالتالي فإن صيغة الربعيات هي كما يلي:
![]()
يرجى ملاحظة: هذه الصيغة تخبرنا بموضع الربيع، وليس قيمة الربع. سيكون الربع هو البيانات الموجودة في الموضع الذي حصلت عليه الصيغة.
ومع ذلك، في بعض الأحيان نتيجة هذه الصيغة تعطينا عددًا عشريًا. ولذلك يجب علينا التمييز بين حالتين اعتمادًا على ما إذا كانت النتيجة رقمًا عشريًا أم لا:
- إذا كانت نتيجة الصيغة رقمًا بدون جزء عشري ، فإن الربع هو البيانات الموجودة في الموضع الذي توفره الصيغة أعلاه.
- إذا كانت نتيجة الصيغة رقمًا بجزء عشري ، فسيتم حساب القيمة الربعية باستخدام الصيغة التالية:
![]()
حيث x i و x i+1 هما أرقام المواضع التي يقع بينها الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى، و d هو الجزء العشري من الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى.
الآن، ربما يكون حساب الأرباع أمرًا معقدًا جدًا بالنسبة لك، لأن هناك الكثير من الأشياء التي يجب أخذها في الاعتبار. ولكن مع المثالين في القسم التالي، سترى كيف أن الأمر في الواقع بسيط للغاية.
ملاحظة : في المجتمع العلمي، لا يوجد إجماع حول كيفية حساب الربعيات، لذلك يمكنك العثور على كتاب إحصائي يشرح ذلك بشكل مختلف قليلاً.
أمثلة على حساب الربعيات
لفهم كيفية حساب الربعيات بشكل كامل، ستجد تمرينين تم حلهما أدناه. في الحالة الأولى، تكون الأرباع صحيحة، وفي الثانية تكون الأرباع أرقامًا عشرية، لذا يمكنك معرفة أي حالتين يمكنك العثور عليهما.
مثال 1
- احسب الأرباع الثلاثة لمجموعة البيانات التالية:

كما رأينا أعلاه، فإن صيغة تحديد الربعيات هي:
![]()
في هذه الحالة n ، العدد الإجمالي للملاحظات هو 15، لذلك يجب علينا استبدال n بـ 15 و k بـ 1 للعثور على الربع الأول:
![]()
ولذلك، فإن الربيع الأول هو الرقم الموجود في الموضع الرابع من قائمة القيم المرتبة، وهو في هذه الحالة 39.
وبنفس الطريقة، نحسب الربع الثاني عن طريق استبدال المعامل k بـ 2:
![]()
وبالتالي فإن الربع 2 هو الرقم الثامن في القائمة التي تم فرزها، والذي يتوافق مع القيمة 48.
أخيرًا، نطبق الصيغة مرة أخيرة حيث k =3 لحساب الربع الثالث:
![]()
الربع 3 يتوافق مع البيانات الموجودة في المركز الثاني عشر، أي 60.
مثال 2
- أوجد الأرباع الثلاثة لسلسلة البيانات التالية:

في هذا المثال الثاني، لدينا 24 ملاحظة، وبالتالي فإن الأرقام التي تم الحصول عليها من الصيغة الربعية ستكون عشرية.
نقوم أولاً بحساب موضع الربع الأول عن طريق استبدال k بـ 1 في الصيغة العامة:
![]()
![]()
لكننا حصلنا على الرقم العشري 6.25، لذا فإن الربع الأول يقع بين البيانات السادسة والسابعة، وهما 22 و25 على التوالي. لذلك، لحساب الربع الدقيق نحتاج إلى تطبيق الصيغة التالية:
![]()
في هذه الحالة x i هو 22، x i+1 25 و d هو الجزء العشري من الرقم الذي تم الحصول عليه، أي 0.25. حتى الآن:
![]()
والآن نقوم بنفس الإجراء لإيجاد الربع الثاني:
![]()
مرة أخرى، نحصل على رقم عشري من الصيغة، وهو في هذه الحالة 12.5. ولذلك يجب علينا استخدام نفس الصيغة مع الرقمين الثاني عشر والثالث عشر في جدول البيانات، والذي يتوافق مع 49 و 50:
![]()
وأخيراً نكرر نفس العملية للحصول على الربع الثالث:
![]()
لكن الرقم 18.75 يقع بين الرقمين 18 و19، وبالتالي فإن الربع الثالث سيكون بين قيم هذين الموضعين (71 و73). وبتعبير أدق، ستكون هذه هي القيمة التي نحصل عليها من التعبير التالي:
![]()
حاسبة الربع
أدخل مجموعة بيانات إحصائية في الآلة الحاسبة أدناه لحساب الربعيات. يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.
الربعيات في البيانات المجمعة
لحساب الربعيات عندما يتم تجميع البيانات في فترات، نحتاج أولاً إلى العثور على الفاصل الزمني أو الحاوية التي يقع فيها الربع باستخدام الصيغة التالية:
![]()
وبالتالي فإن الربع سيكون في الفترة التي يكون تكرارها التراكمي المطلق أكبر مباشرة من الرقم الذي تم الحصول عليه بالتعبير السابق.
وبمجرد أن نعرف الفترة التي ينتمي إليها الربيع، يجب علينا تطبيق الصيغة التالية للعثور على القيمة الدقيقة للربيع:
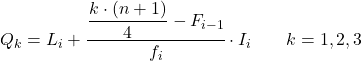
ذهب:
- L i هو الحد الأدنى للفاصل الزمني الذي يقع فيه الربع.
- n هو العدد الإجمالي للملاحظات.
- F i-1 هو التردد المطلق التراكمي للفاصل الزمني السابق.
- f i هو التكرار المطلق للفاصل الزمني الذي يقع فيه الربع.
- I i هو عرض الفاصل الربيعي.
على سبيل المثال، إليك تمرين لحساب الربعيات في سلسلة من البيانات المجمعة:

لحساب الربع الأول، يجب عليك أولا تحديد الفاصل الزمني الذي يقع فيه. للقيام بذلك، نطبق الصيغة التالية:
![]()
![]()
لذا فإن الربيع الأول سيكون في الفترة التي يكون تكرارها المطلق التراكمي أكبر مباشرة من 7.75، وفي هذه الحالة هي الفترة [50.60) التي يكون ترددها المطلق التراكمي 15. وبمجرد أن نعرف الفترة الربيعية، نستخدم صيغة العملية الثانية :
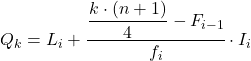
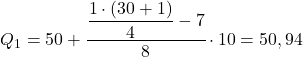
نطبق نفس الإجراء مرة أخرى للحصول على الربع الثاني. نحدد أولاً الفترة التي يقع فيها الربع:
![]()
الفاصل الزمني الذي يكون تردده المطلق التراكمي أكبر مباشرة من 15.5 هو [60.70)، مع تردد مطلق تراكمي قدره 26. وبالتالي فإن الربع الثاني هو:
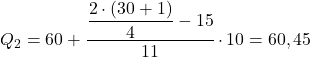
وأخيرًا، نكرر العملية لإيجاد الربيع الثالث. نحسب أولاً الفترة التي تحتوي على الربع:
![]()
والتكرار المطلق التراكمي مباشرة فوق 23.25 هو 26، وبالتالي فإن المدى الربعي الثالث هو [60.70). ولذلك فإننا نطبق الصيغة لحساب الربع مع هذه الفترة:
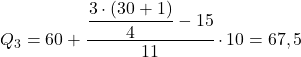
ما هي الأرباع المستخدمة ل؟
تعتبر الربعيات مقياسًا للموضع، لذا يتم استخدامها لمعرفة كيفية تحديد موضع البيانات. بمعنى آخر، تتيح لنا قيم الأرباع الثلاثة معرفة ما إذا كان عنصر البيانات العشوائي في العينة كبيرًا جدًا أو صغيرًا جدًا أو إذا كان ذا قيمة متوسطة.
إذا أخذنا عشوائيًا جزءًا من البيانات من العينة، فيمكننا معرفة ما إذا كانت قيمتها مرتفعة أم منخفضة من خلال مقارنتها بالربيعات. إذا كانت قيمة البيانات العشوائية أقل من الربع الأول، فستكون قيمة صغيرة، أما إذا كانت قيمتها أكبر من الربع الثالث، فستكون قيمة كبيرة. وبالمثل، إذا كانت قيمة البيانات المذكورة بين الربع الأول والثالث، فهي قيمة متوسطة.
من ناحية أخرى، تُستخدم الأرباع أيضًا لحساب مقاييس إحصائية أخرى، مثل النطاق الربيعي (أو المدى الربيعي)، ولعمل الرسوم البيانية، مثل المخطط الصندوقي والشريطي (أو مخطط الصندوق).