كيفية تنفيذ التدابير المتكررة anova في spss

يتم استخدام المقاييس المتكررة ANOVA لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات أو أكثر تظهر فيها نفس المواضيع في كل مجموعة أم لا.

يشرح هذا البرنامج التعليمي كيفية إجراء تحليل التباين (ANOVA) للقياسات المتكررة في اتجاه واحد في برنامج SPSS.

مثال: التدابير المتكررة ANOVA في SPSS

يريد الباحثون معرفة ما إذا كانت أربعة أدوية مختلفة تسبب أوقات رد فعل مختلفة. ولاختبار ذلك، قاموا بقياس أوقات رد فعل خمسة مرضى لأربعة أدوية مختلفة. نظرًا لأنه يتم قياس كل مريض على كل من الأدوية الأربعة، فسوف نستخدم تحليل التباين (ANOVA) للقياسات المتكررة لتحديد ما إذا كان متوسط وقت التفاعل يختلف بين الأدوية.

أكمل الخطوات التالية لتنفيذ التدابير المتكررة ANOVA في SPSS.

الخطوة 1: أدخل البيانات.

أدخل البيانات التالية التي توضح زمن الاستجابة (بالثواني) لخمسة مرضى للأدوية الأربعة:

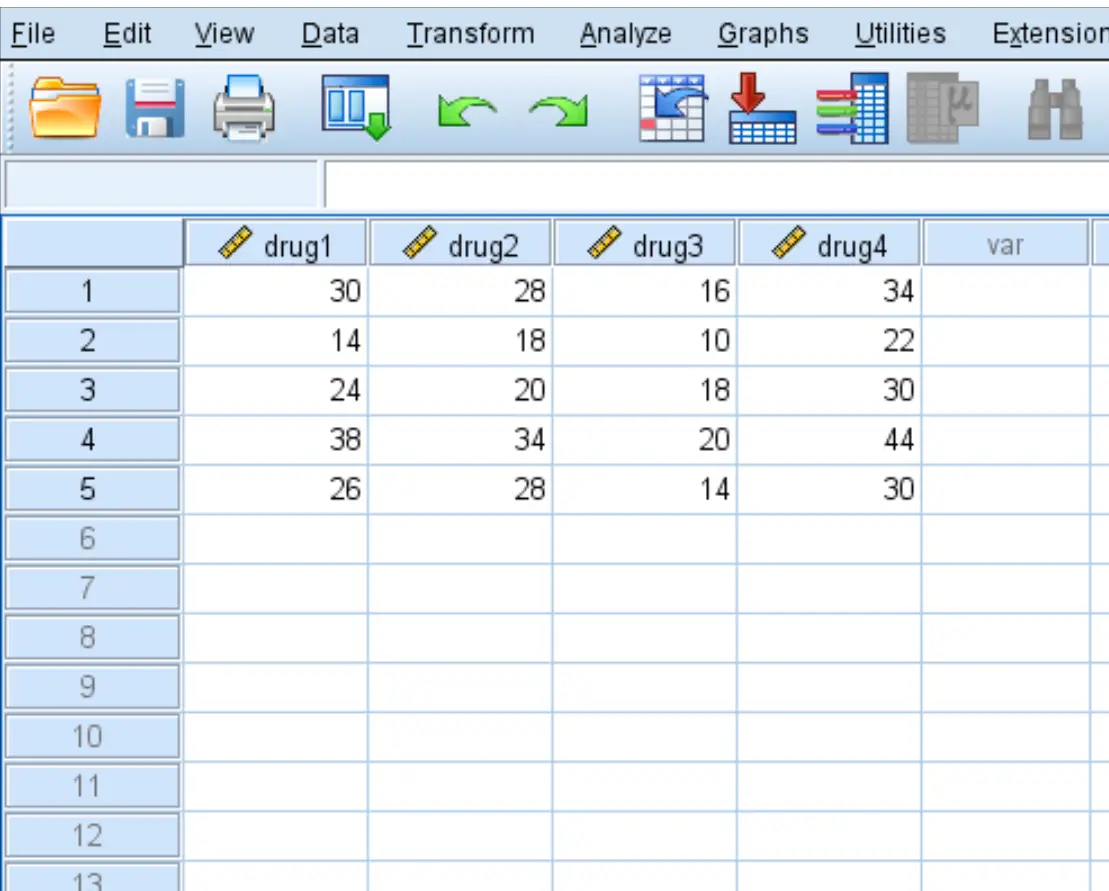
الخطوة 2: تنفيذ التدابير المتكررة ANOVA.

انقر فوق علامة التبويب تحليل ، ثم النموذج الخطي العام ، ثم القياسات المتكررة :

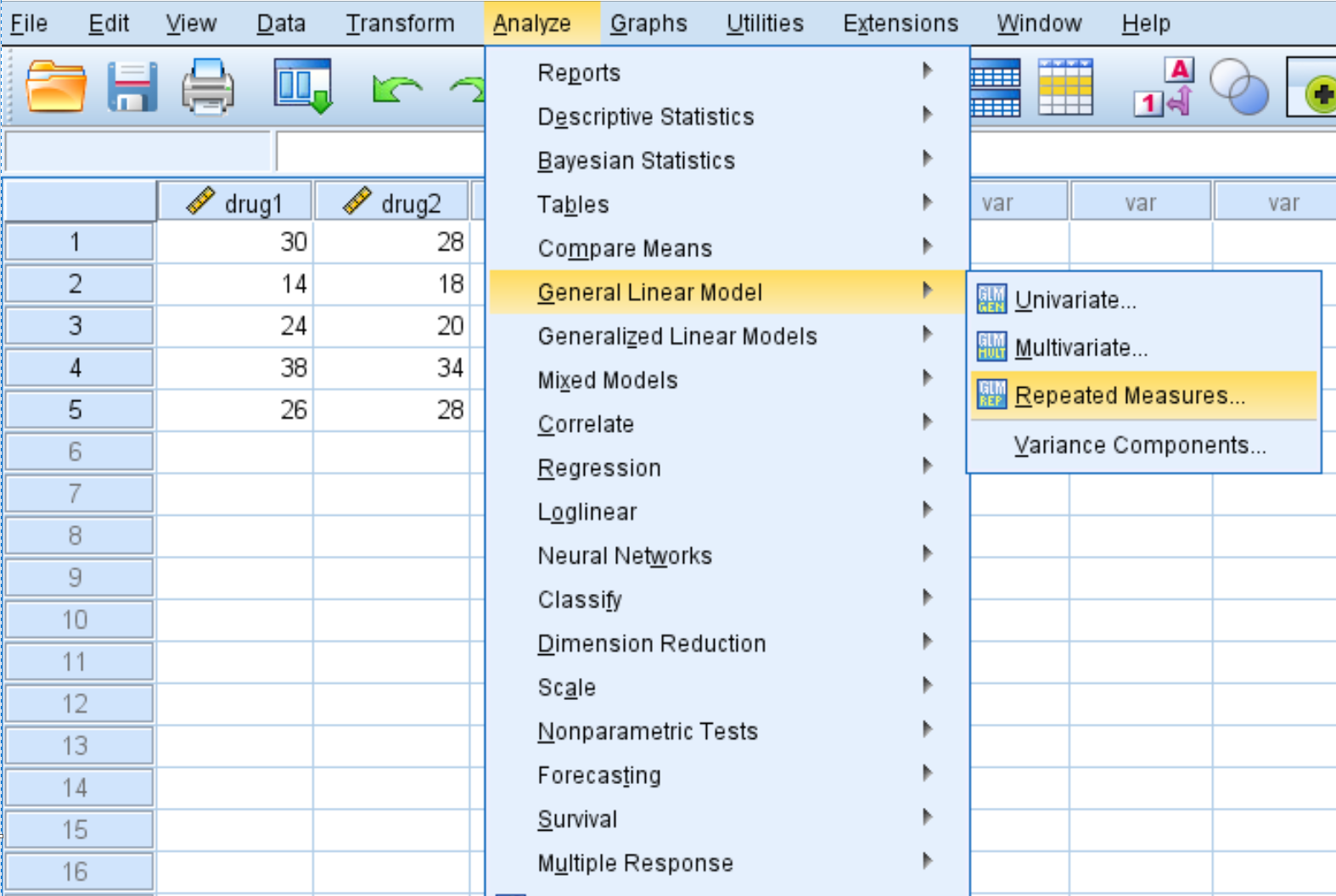
في النافذة الجديدة التي تظهر، أدخل الدواء لاسم العامل داخل الموضوع. اكتب 4 لعدد المستويات (نظرًا لأن كل موضوع دراسة اختبر 4 أدوية مختلفة)، ثم انقر فوق “إضافة” . اكتب ResponseTime لاسم القياس ، ثم انقر فوق إضافة . وأخيرا، انقر فوق تعيين .

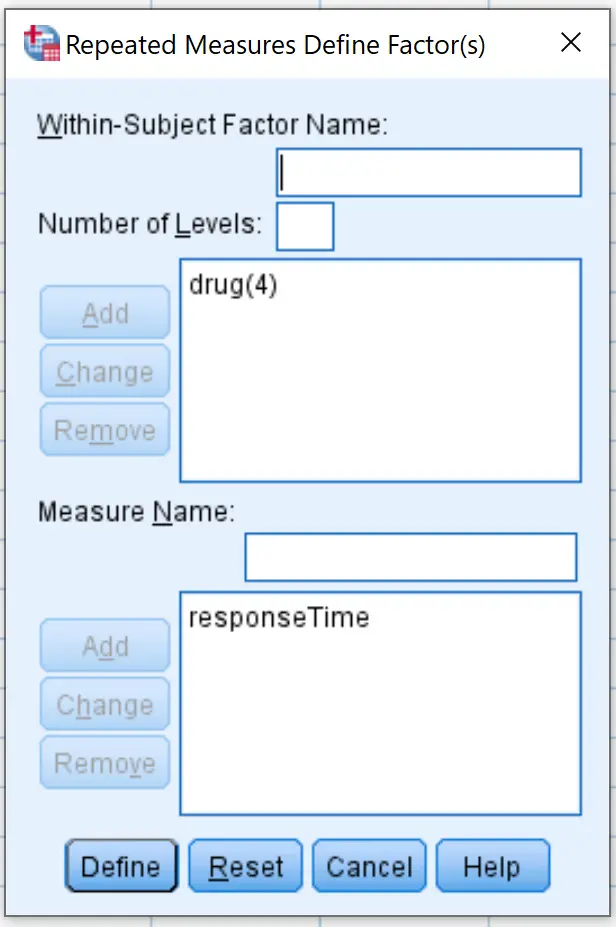
في النافذة الجديدة التي تظهر، اسحب كل متغير من متغيرات الدواء الأربعة إلى المنطقة المسماة “متغيرات داخل المواضيع” :

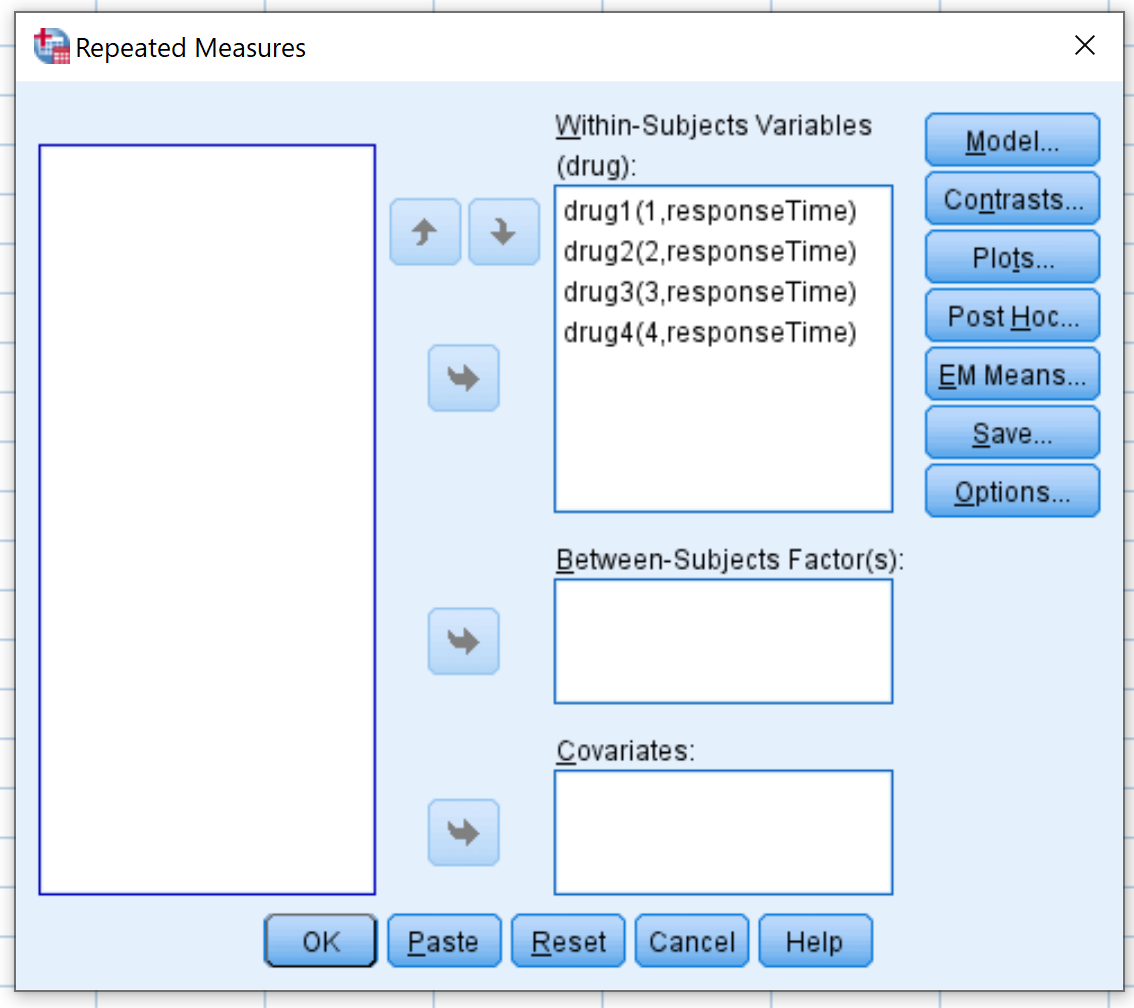
بعد ذلك، انقر فوق المؤامرات . اسحب الدواء المتغير إلى المنطقة المسماة “المحور الأفقي” . ثم انقر فوق إضافة . ثم انقر فوق “متابعة” .

بعد ذلك، انقر فوق وسائل EM . اسحب متغير الدواء إلى المربع المسمى Show Means For . ثم حدد المربع بجوار مقارنة التأثيرات الرئيسية وحدد Bonferroni من القائمة المنسدلة. ثم انقر فوق “متابعة” .

وأخيرا، انقر فوق موافق .

الخطوة الثانية: تفسير النتائج.

بمجرد النقر فوق موافق ، ستظهر نتائج التدابير المتكررة ANOVA. وإليك كيفية تفسير النتيجة:

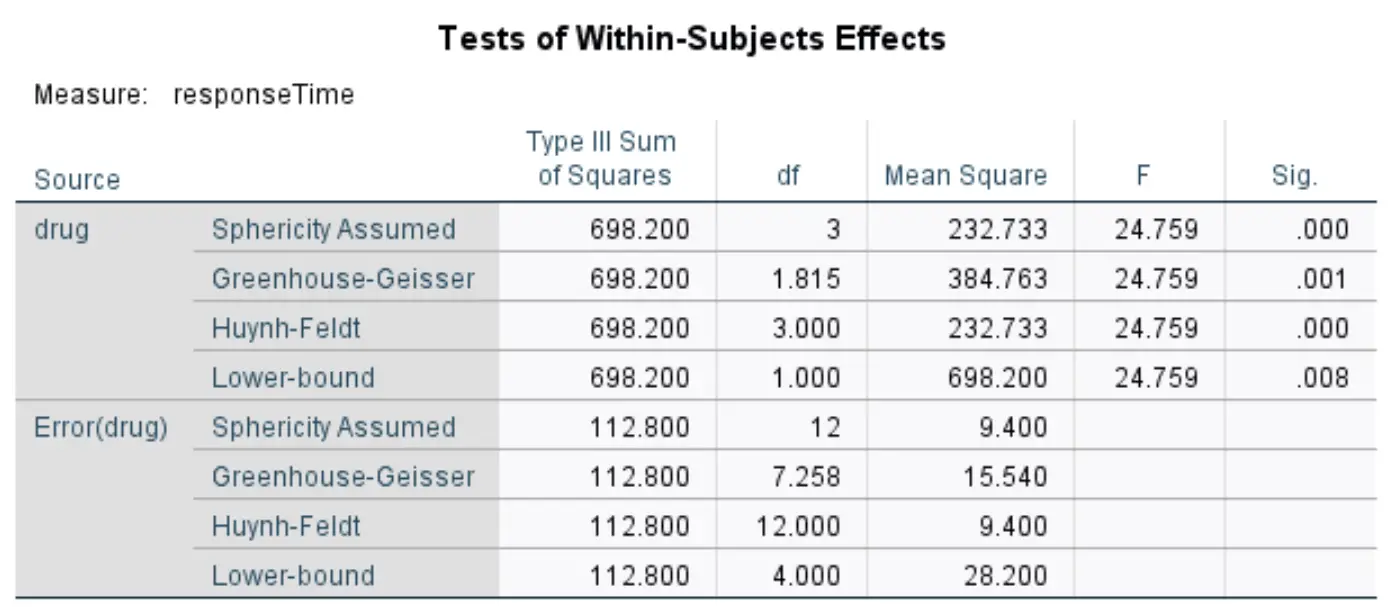
اختبارات التأثيرات داخل المواضيع

يعرض هذا الجدول إحصائيات F الإجمالية والقيمة p المقابلة من المقاييس المتكررة ANOVA. نستخدم عمومًا قيمًا من السطر المسمى Greenhouse-Geisser .

وفقًا لهذا الخط، تكون إحصائيات F هي 24.759 والقيمة p المقابلة هي 0.001 . وبما أن هذه القيمة p أقل من 0.05، يمكننا رفض الفرضية الصفرية ونستنتج أن هناك فرق ذو دلالة إحصائية في متوسط أوقات الاستجابة بين الأدوية الأربعة.

المقارنات الزوجية

وبما أننا رفضنا فرضية العدم، فهذا يعني أن متوسطي مجموعتين على الأقل مختلفان. لتحديد مجموعات الوسائل المختلفة، يمكننا استخدام هذا الجدول الذي يعرض المقارنات الزوجية بين كل دواء.

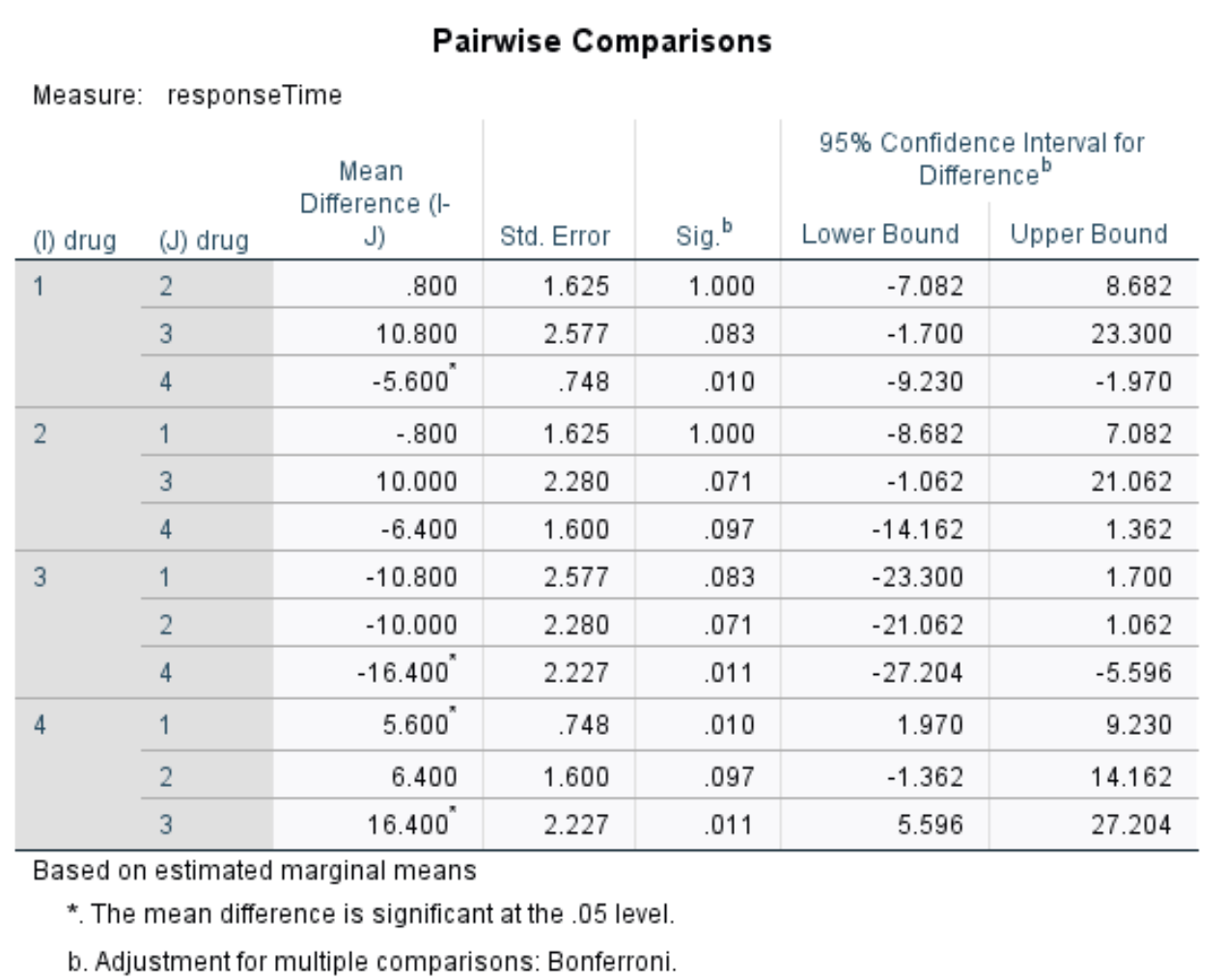
في الجدول يمكننا أن نرى القيم الاحتمالية للمقارنات التالية:

• المخدرات 1 مقابل المخدرات 2 | القيمة p = 1.000
• المخدرات 1 مقابل المخدرات 3 | القيمة p = 0.083
• المخدرات 1 مقابل المخدرات 4 | القيمة p = 0.010
• المخدرات 2 مقابل المخدرات 3 | القيمة p = 0.071
• المخدرات 2 مقابل المخدرات 4 | القيمة p = 0.097
• المخدرات 3 مقابل المخدرات 4 | القيمة p = 0.011

القيم p الوحيدة التي تقل عن 0.05 هي للعقار 1 مقابل الدواء 4 والدواء 3 مقابل الدواء 4. وجميع المقارنات الأخرى لها قيم p أكبر من 0.05.

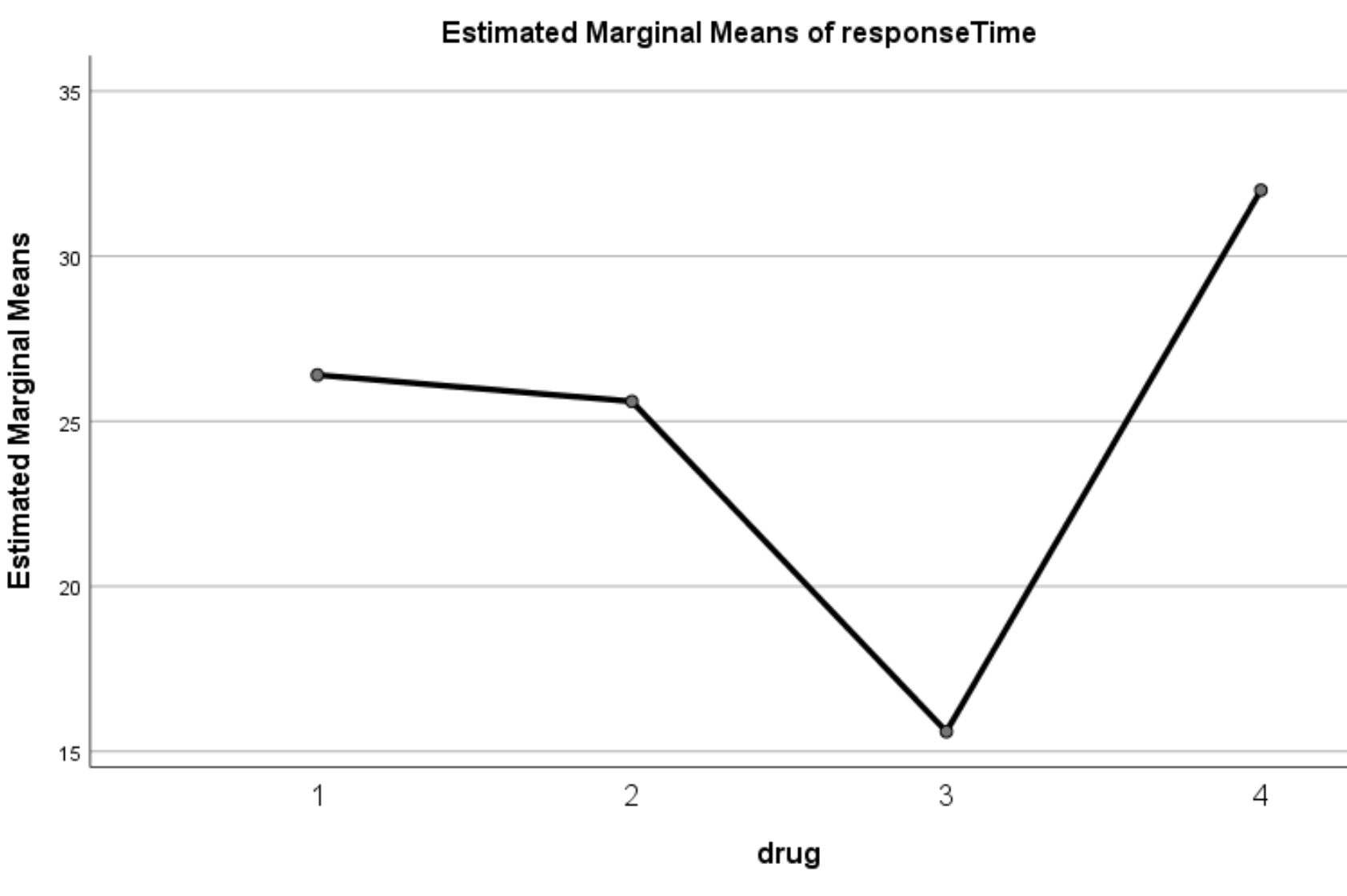
رسم بياني للوسائل الهامشية المقدرة

يعرض هذا الرسم البياني متوسط أوقات الاستجابة المقدرة لكل دواء. من الرسم البياني، يمكننا أن نرى بوضوح أن أوقات الاستجابة تباينت بشكل كبير بين الأدوية الأربعة المختلفة:

الخطوة 3: الإبلاغ عن النتائج.

وأخيرا، يمكننا الإبلاغ عن نتائج التدابير المتكررة ANOVA. فيما يلي مثال لكيفية القيام بذلك:

تم إجراء ANOVA للتدابير المتكررة في اتجاه واحد لتحديد ما إذا كان متوسط وقت رد الفعل لدى المرضى يختلف بين أربعة أدوية مختلفة.

وكشفت التدابير المتكررة في اتجاه واحد ANOVA أن نوع الدواء المستخدم أدى إلى فروق ذات دلالة إحصائية في زمن الاستجابة (F = 24.75887، ع = 0.001).

كشف اختبار Bonferroni لإجراء مقارنات متعددة عن وجود فروق ذات دلالة إحصائية في أوقات الاستجابة بين المرضى الذين يتناولون الدواء 1 والدواء 4 وكذلك الدواء 3 والدواء 4.