كيفية حساب القيمة المتوقعة لـ x^3
بالنسبة للمتغير العشوائي ، المشار إليه بـ X، يمكنك استخدام الصيغة التالية لحساب القيمة المتوقعة لـ X 3 :
ه(X 3 ) = Σx 3 * ص(x)
ذهب:
- Σ : رمز يعني “المجموع”
- x : قيمة المتغير العشوائي
- p(x) : احتمال أن يأخذ المتغير العشوائي قيمة معينة
يوضح المثال التالي كيفية استخدام هذه الصيغة عمليًا.
مثال: حساب القيمة المتوقعة لـ X 3
لنفترض أن لدينا جدول التوزيع الاحتمالي التالي الذي يصف احتمال وجود متغير عشوائي،
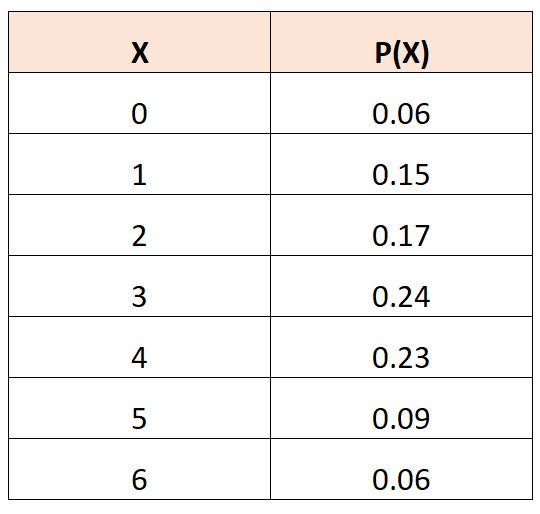
لحساب القيمة المتوقعة لـ X 3 يمكننا استخدام الصيغة التالية:
ه(X 3 ) = Σx 3 * ص(x)
ه(X 3 ) = (0) 3 *.06 + (1) 3 *.15 + (2) 3 *.17 + (3) 3 *.24 + (4) 3 *.23 + (5) 3 *.09 + (6) 3 *.06
ه(X 3 ) = 0 + 0.15 + 0.1.36 + 6.48 + 14.72 + 11.25 + 12.96
ه(× 3 ) = 45.596
القيمة المتوقعة لـ X 3 هي 45,596 .
لاحظ أن هذا المتغير العشوائي هو متغير عشوائي منفصل ، مما يعني أنه يمكن أن يأخذ فقط عددًا محدودًا من القيم.
إذا كان X متغير عشوائي مستمر ، يجب علينا استخدام الصيغة التالية لحساب القيمة المتوقعة لـ X 3 :
E(X 3 ) = ∫ x 3 f(x)dx
ذهب:
- ∫: رمز يعني “التكامل”
- f(x) : يستمر ملف pdf للمتغير العشوائي
عند حساب القيمة المتوقعة ل
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في الإحصائيات:
كيفية العثور على متوسط التوزيع الاحتمالي
كيفية العثور على الانحراف المعياري للتوزيع الاحتمالي
كيفية العثور على التباين في التوزيع الاحتمالي
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر