كيفية رسم منحنى roc في بايثون (خطوة بخطوة)

الانحدار اللوجستي هو طريقة إحصائية نستخدمها لتناسب نموذج الانحدار عندما يكون متغير الاستجابة ثنائيًا. لتقييم مدى ملاءمة نموذج الانحدار اللوجستي لمجموعة البيانات، يمكننا النظر إلى المقياسين التاليين:

• الحساسية: احتمال أن يتنبأ النموذج بنتيجة إيجابية لملاحظة ما عندما تكون النتيجة إيجابية بالفعل. ويسمى هذا أيضًا “المعدل الإيجابي الحقيقي”.
• الخصوصية: احتمال أن يتنبأ النموذج بنتيجة سلبية لملاحظة ما عندما تكون النتيجة سلبية بالفعل. ويسمى هذا أيضًا “المعدل السلبي الحقيقي”.

إحدى الطرق لتصور هذين القياسين هي إنشاء منحنى ROC ، والذي يرمز إلى منحنى “خاصية تشغيل جهاز الاستقبال”. هذا رسم بياني يعرض حساسية وخصوصية نموذج الانحدار اللوجستي.

يوضح المثال التالي خطوة بخطوة كيفية إنشاء وتفسير منحنى ROC في بايثون.

الخطوة 1: استيراد الحزم اللازمة

أولاً، سنقوم باستيراد الحزم اللازمة لإجراء الانحدار اللوجستي في بايثون:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

الخطوة 2: ملاءمة نموذج الانحدار اللوجستي

بعد ذلك، سنقوم باستيراد مجموعة بيانات وملائمة نموذج الانحدار اللوجستي لها:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/- Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0) 

#instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

الخطوة 3: ارسم منحنى ROC

بعد ذلك، سنقوم بحساب المعدل الإيجابي الحقيقي والمعدل الإيجابي الخاطئ وإنشاء منحنى ROC باستخدام حزمة تصور بيانات Matplotlib:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr)
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. show () 

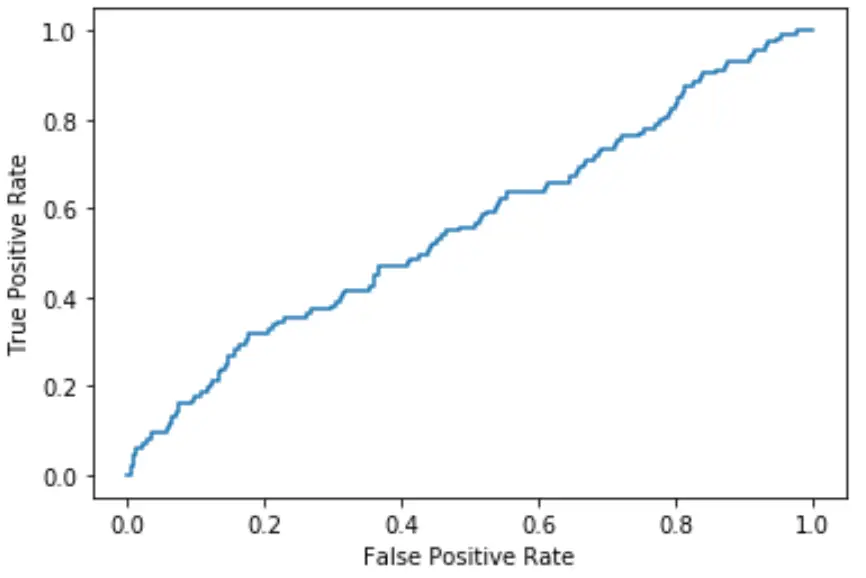
كلما اقترب المنحنى من الزاوية اليسرى العليا من المخطط، كلما كان النموذج قادرًا على تصنيف البيانات إلى فئات بشكل أفضل.

كما نرى من الرسم البياني أعلاه، فإن نموذج الانحدار اللوجستي هذا يقوم بعمل سيئ جدًا في فرز البيانات إلى فئات.

ولقياس ذلك، يمكننا حساب المساحة تحت المنحنى AUC، والتي تخبرنا بمقدار قطعة الأرض الموجودة تحت المنحنى.

كلما اقتربت AUC من 1، كان النموذج أفضل. النموذج الذي تبلغ فيه المساحة تحت المنحنى 0.5 ليس أفضل من النموذج الذي يقوم بتصنيفات عشوائية.

الخطوة 4: حساب الجامعة الأمريكية بالقاهرة

يمكننا استخدام الكود التالي لحساب AUC للنموذج وعرضه في الركن الأيمن السفلي من مخطط ROC:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. legend (loc=4)
plt. show () 

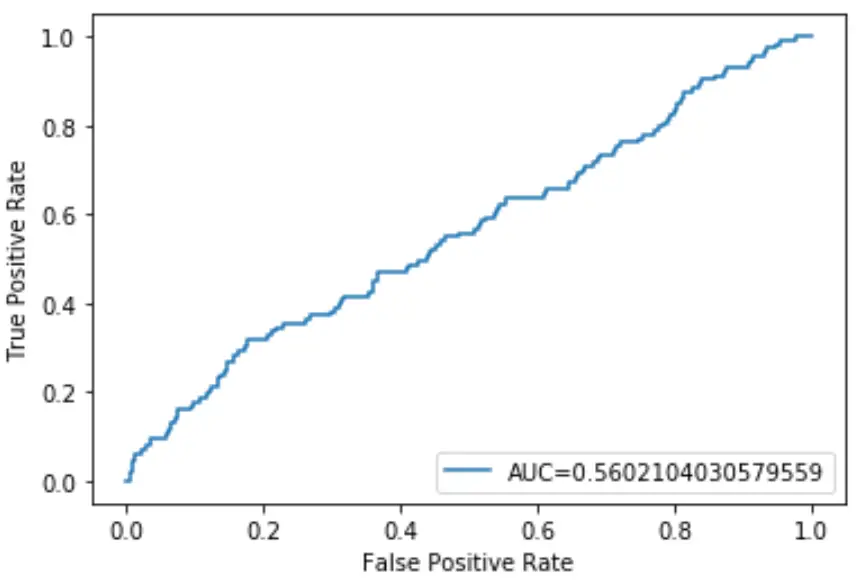
وتبين أن AUC لنموذج الانحدار اللوجستي هذا هو 0.5602 . وبما أن هذا الرقم مغلق عند 0.5، فهذا يؤكد أن النموذج يقوم بعمل ضعيف في تصنيف البيانات.

ذات صلة: كيفية رسم منحنيات ROC المتعددة في بايثون