كيفية إجراء تحليل ثنائي المتغير في لغة r (مع أمثلة)

يشير مصطلح التحليل ثنائي المتغير إلى تحليل متغيرين. يمكنك تذكر ذلك لأن البادئة “bi” تعني “اثنين”.

الهدف من التحليل ثنائي المتغير هو فهم العلاقة بين متغيرين

هناك ثلاث طرق شائعة لإجراء التحليل ثنائي المتغير:

1. نقطة الغيوم

2. معاملات الارتباط

3. الانحدار الخطي البسيط

يوضح المثال التالي كيفية إجراء كل نوع من هذه الأنواع من التحليل ثنائي المتغير باستخدام مجموعة البيانات التالية التي تحتوي على معلومات حول متغيرين: (1) الساعات المستغرقة في الدراسة و (2) درجات الاختبار التي حصل عليها 20 طالبًا مختلفًا:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. نقطة الغيوم

يمكننا استخدام بناء الجملة التالي لإنشاء مخطط مبعثر لساعات الدراسة مقابل درجة الامتحان في R:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

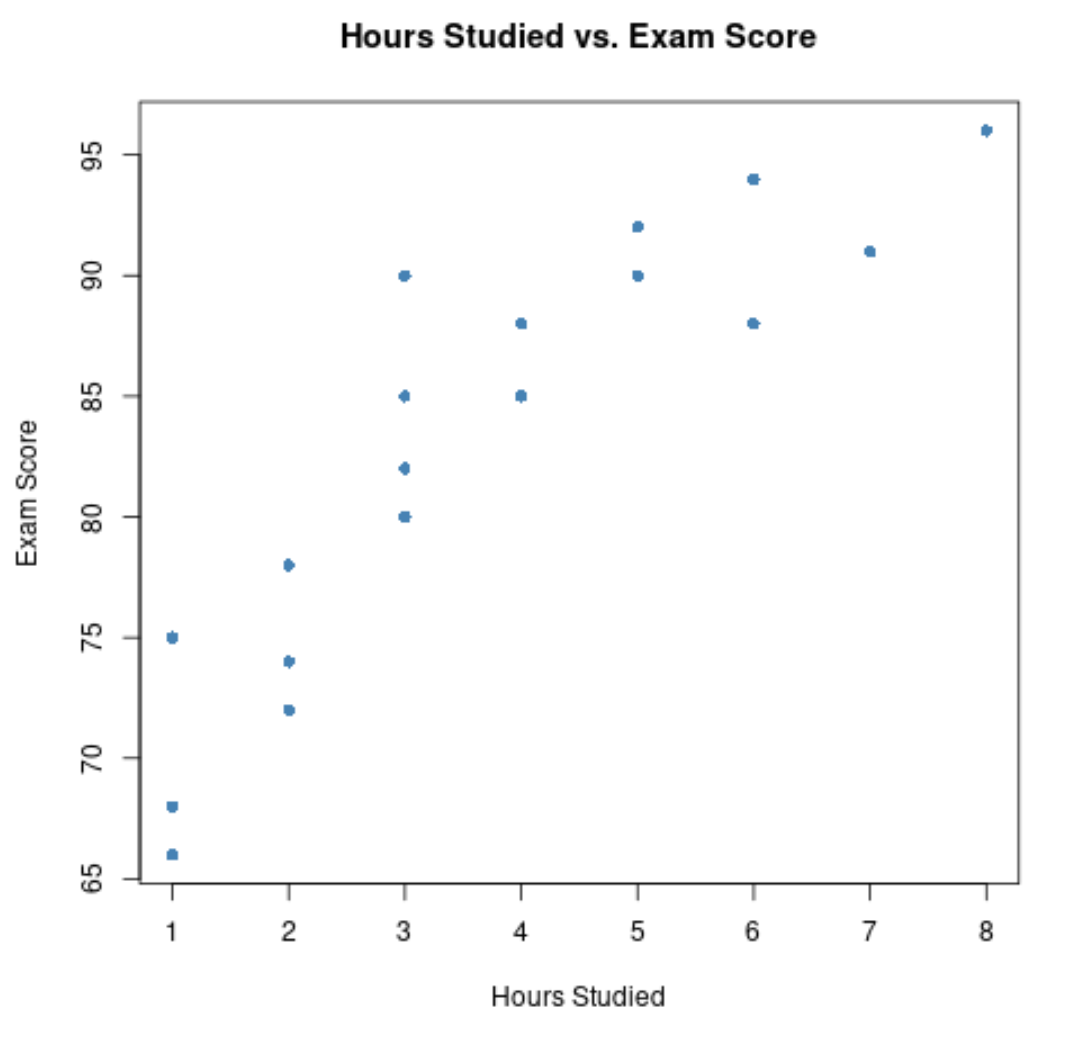
يُظهر المحور “س” الساعات التي تمت دراستها، بينما يُظهر المحور “ص” الدرجة التي تم الحصول عليها في الاختبار.

ويبين الرسم البياني أن هناك علاقة إيجابية بين المتغيرين: فكلما زاد عدد ساعات الدراسة، تميل درجات الامتحانات أيضا إلى الارتفاع.

2. معاملات الارتباط

معامل ارتباط بيرسون هو وسيلة لقياس العلاقة الخطية بين متغيرين.

يمكننا استخدام الدالة cor() في R لحساب معامل ارتباط بيرسون بين متغيرين:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

وتبين أن معامل الارتباط هو 0.891 .

هذه القيمة قريبة من 1، مما يشير إلى وجود علاقة إيجابية قوية بين ساعات الدراسة ودرجة الامتحان.

3. الانحدار الخطي البسيط

الانحدار الخطي البسيط هو طريقة إحصائية يمكننا استخدامها للعثور على معادلة الخط الذي “يناسب” مجموعة من البيانات بشكل أفضل، والتي يمكننا بعد ذلك استخدامها لفهم العلاقة الدقيقة بين متغيرين.

يمكننا استخدام الدالة lm() في R لتناسب نموذج الانحدار الخطي البسيط لساعات الدراسة ونتائج الامتحانات المستلمة:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

وتبين أن معادلة الانحدار المجهزة هي:

درجة الامتحان = 69.0734 + 3.8471*(ساعات الدراسة)

وهذا يخبرنا أن كل ساعة إضافية تتم دراستها ترتبط بمتوسط زيادة قدرها 3.8471 في درجة الامتحان.

يمكننا أيضًا استخدام معادلة الانحدار المجهزة للتنبؤ بالنتيجة التي سيحصل عليها الطالب بناءً على إجمالي عدد الساعات المدروسة.

على سبيل المثال الطالب الذي يدرس لمدة 3 ساعات يجب أن يحصل على 81.6147 :

• درجة الامتحان = 69.0734 + 3.8471*(ساعات الدراسة)
• درجة الامتحان = 69.0734 + 3.8471*(3)
• نتيجة الامتحان = 81.6147

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول التحليل ثنائي المتغير:

مقدمة للتحليل ثنائي المتغير
5 أمثلة للبيانات ثنائية المتغير في الحياة الحقيقية
مقدمة للانحدار الخطي البسيط