تركيب المنحنى في بايثون (مع أمثلة)

في كثير من الأحيان قد ترغب في ملاءمة منحنى لمجموعة بيانات في بايثون.

يشرح المثال التالي خطوة بخطوة كيفية ملاءمة المنحنيات مع البيانات في Python باستخدام الدالة numpy.polyfit() وكيفية تحديد المنحنى الذي يناسب البيانات بشكل أفضل.

الخطوة 1: إنشاء البيانات وتصورها

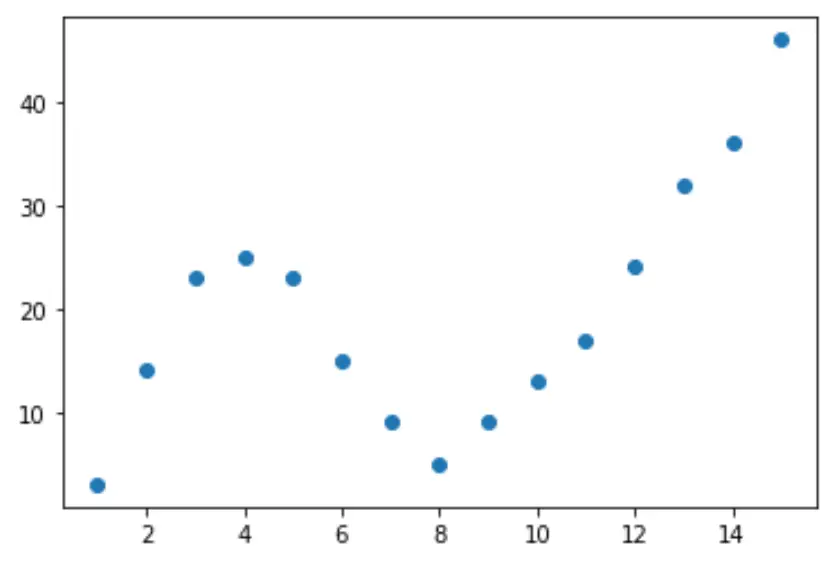
لنبدأ بإنشاء مجموعة بيانات مزيفة، ثم ننشئ مخططًا مبعثرًا لتصور البيانات:

 import pandas as pd
import matplotlib. pyplot as plt

#createDataFrame
df = pd. DataFrame ({' x ': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
                   ' y ': [3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46]})

#create scatterplot of x vs. y
plt. scatter (df. x , df. y ) 

الخطوة 2: ضبط منحنيات متعددة

دعونا بعد ذلك نلائم عدة نماذج انحدار متعددة الحدود مع البيانات ونتصور منحنى كل نموذج في نفس المخطط:

 import numpy as np

#fit polynomial models up to degree 5
model1 = np. poly1d (np. polyfit (df. x , df. y , 1))
model2 = np. poly1d (np. polyfit (df. x , df. y , 2))
model3 = np. poly1d (np. polyfit (df. x , df. y , 3))
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))
model5 = np. poly1d (np. polyfit (df. x , df. y , 5))

#create scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial lines to scatterplot 
plt. plot (polyline, model1(polyline), color=' green ')
plt. plot (polyline, model2(polyline), color=' red ')
plt. plot (polyline, model3(polyline), color=' purple ')
plt. plot (polyline, model4(polyline), color=' blue ')
plt. plot (polyline, model5(polyline), color=' orange ')
plt. show ()

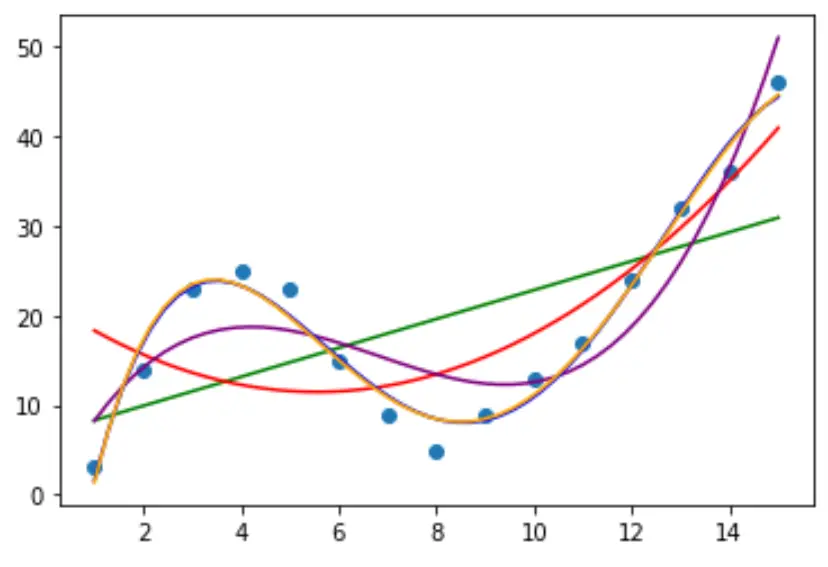
لتحديد المنحنى الذي يناسب البيانات بشكل أفضل، يمكننا أن ننظر إلى مربع R المعدل لكل نموذج.

تخبرنا هذه القيمة بنسبة التباين في متغير الاستجابة الذي يمكن تفسيره بواسطة متغير (متغيرات) التوقع في النموذج، مع تعديلها لعدد متغيرات التوقع.

 #define function to calculate adjusted r-squared
def adjR(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar)**2)
    sstot = np. sum ((y - ybar)**2)
    results[' r_squared '] = 1- (((1-(ssreg/sstot))*(len(y)-1))/(len(y)-degree-1))

    return results

#calculated adjusted R-squared of each model
adjR(df. x , df. y , 1)
adjR(df. x , df. y , 2)
adjR(df. x , df. y , 3)
adjR(df. x , df. y , 4)
adjR(df. x , df. y , 5)

{'r_squared': 0.3144819}
{'r_squared': 0.5186706}
{'r_squared': 0.7842864}
{'r_squared': 0.9590276}
{'r_squared': 0.9549709}

من النتيجة، يمكننا أن نرى أن النموذج الذي يحتوي على أعلى مربع R معدل هو متعدد الحدود من الدرجة الرابعة، والذي يحتوي على مربع R معدل قدره 0.959 .

الخطوة 3: تصور المنحنى النهائي

أخيرًا، يمكننا إنشاء مخطط مبعثر بمنحنى نموذج متعدد الحدود من الدرجة الرابعة:

 #fit fourth-degree polynomial
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))

#define scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial curve to scatterplot
plt. plot (polyline, model4(polyline), ' -- ', color=' red ')
plt. show ()

يمكننا أيضًا الحصول على معادلة هذا الخط باستخدام الدالة print() :

 print (model4)

          4 3 2
-0.01924x + 0.7081x - 8.365x + 35.82x - 26.52

معادلة المنحنى هي كما يلي:

ص = -0.01924س ⁴ + 0.7081 ^{س 3} – 8.365س ² + 35.82س – 26.52

يمكننا استخدام هذه المعادلة للتنبؤ بقيمة متغير الاستجابة بناءً على المتغيرات المتوقعة في النموذج. على سبيل المثال، إذا كانت x = 4 فإننا نتوقع أن y = 23.32 :

ص = -0.0192(4) ⁴ + 0.7081(4) ³ – 8.365(4) ² + 35.82(4) – 26.52 = 23.32

مصادر إضافية

مقدمة للانحدار متعدد الحدود
كيفية إجراء الانحدار متعدد الحدود في بايثون