تركيب المنحنى في r (مع أمثلة)
في كثير من الأحيان قد ترغب في العثور على المعادلة التي تناسب منحنى R.

يشرح المثال التالي خطوة بخطوة كيفية ملاءمة المنحنيات للبيانات في R باستخدام الدالة poly() وكيفية تحديد المنحنى الذي يناسب البيانات بشكل أفضل.
الخطوة 1: إنشاء البيانات وتصورها
لنبدأ بإنشاء مجموعة بيانات مزيفة، ثم ننشئ مخططًا مبعثرًا لتصور البيانات:
#create data frame df <- data. frame (x=1:15, y=c(3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46)) #create a scatterplot of x vs. y plot(df$x, df$y, pch= 19 , xlab=' x ', ylab=' y ')
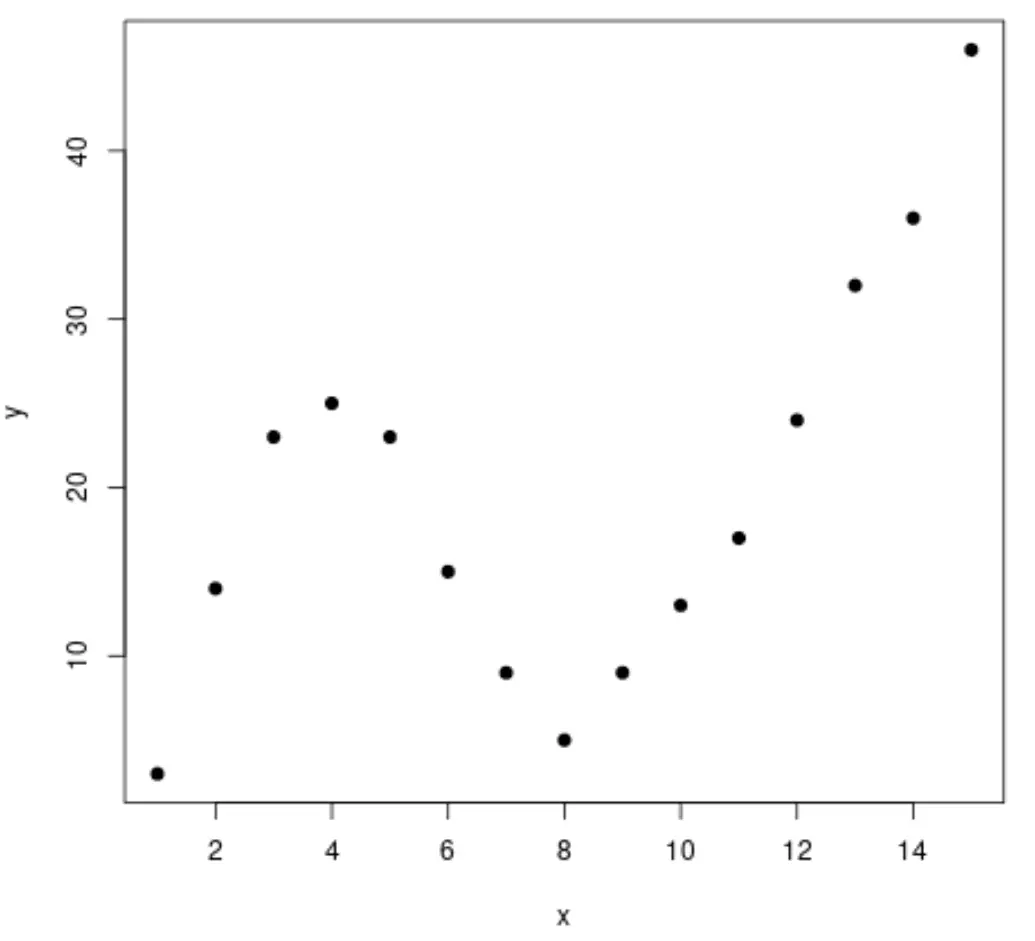
الخطوة 2: ضبط منحنيات متعددة
دعونا بعد ذلك نلائم عدة نماذج انحدار متعددة الحدود مع البيانات ونتصور منحنى كل نموذج في نفس المخطط:
#fit polynomial regression models up to degree 5 fit1 <- lm(y~x, data=df) fit2 <- lm(y~poly(x,2,raw= TRUE ), data=df) fit3 <- lm(y~poly(x,3,raw= TRUE ), data=df) fit4 <- lm(y~poly(x,4,raw= TRUE ), data=df) fit5 <- lm(y~poly(x,5,raw= TRUE ), data=df) #create a scatterplot of x vs. y plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ') #define x-axis values x_axis <- seq(1, 15, length= 15 ) #add curve of each model to plot lines(x_axis, predict(fit1, data. frame (x=x_axis)), col=' green ') lines(x_axis, predict(fit2, data. frame (x=x_axis)), col=' red ') lines(x_axis, predict(fit3, data. frame (x=x_axis)), col=' purple ') lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ') lines(x_axis, predict(fit5, data. frame (x=x_axis)), col=' orange ')
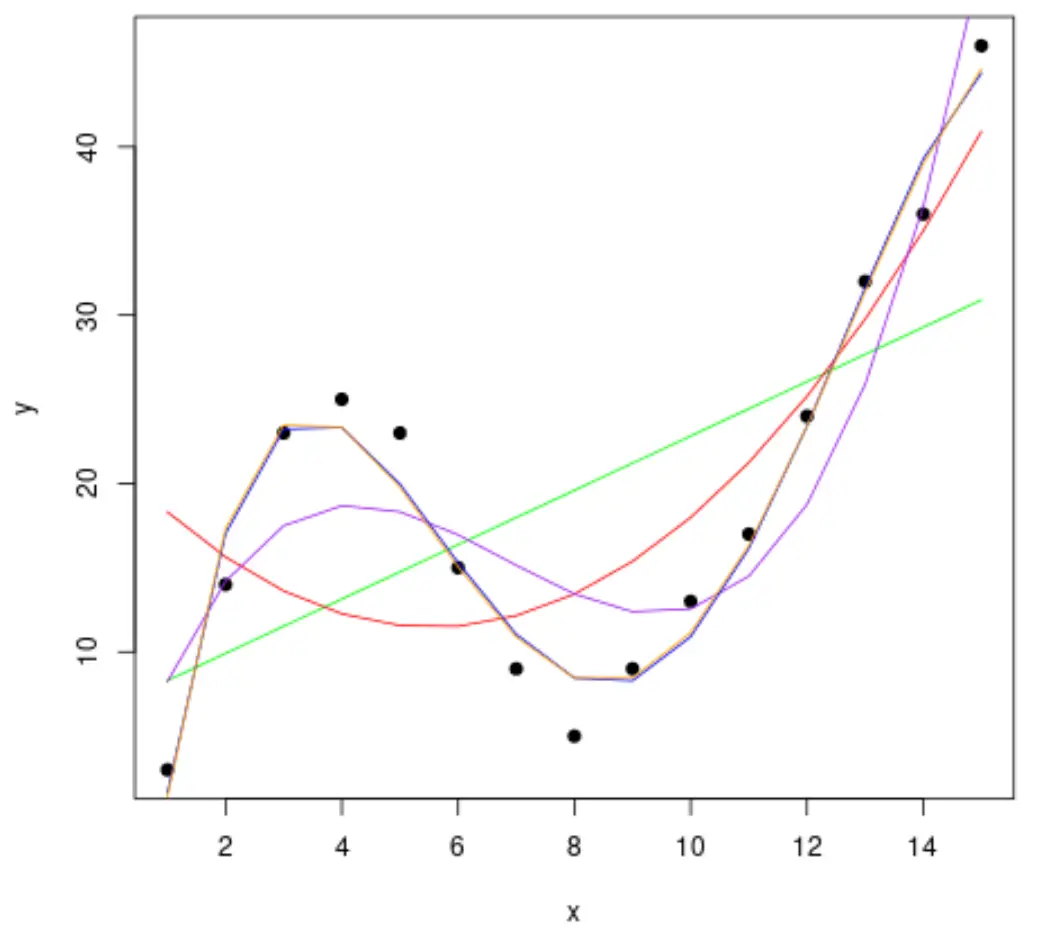
لتحديد المنحنى الذي يناسب البيانات بشكل أفضل، يمكننا أن ننظر إلى مربع R المعدل لكل نموذج.
تخبرنا هذه القيمة بنسبة التباين في متغير الاستجابة الذي يمكن تفسيره بواسطة متغير (متغيرات) التوقع في النموذج، مع تعديلها لعدد متغيرات التوقع.
#calculated adjusted R-squared of each model summary(fit1)$adj. r . squared summary(fit2)$adj. r . squared summary(fit3)$adj. r . squared summary(fit4)$adj. r . squared summary(fit5)$adj. r . squared [1] 0.3144819 [1] 0.5186706 [1] 0.7842864 [1] 0.9590276 [1] 0.9549709
من النتيجة، يمكننا أن نرى أن النموذج الذي يحتوي على أعلى مربع R معدل هو متعدد الحدود من الدرجة الرابعة، والذي يحتوي على مربع R معدل قدره 0.959 .
الخطوة 3: تصور المنحنى النهائي
أخيرًا، يمكننا إنشاء مخطط مبعثر بمنحنى نموذج متعدد الحدود من الدرجة الرابعة:
#create a scatterplot of x vs. y plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ') #define x-axis values x_axis <- seq(1, 15, length= 15 ) #add curve of fourth-degree polynomial model lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')

يمكننا أيضًا الحصول على معادلة هذا الخط باستخدام الدالة Summary() :
summary(fit4)
Call:
lm(formula = y ~ poly(x, 4, raw = TRUE), data = df)
Residuals:
Min 1Q Median 3Q Max
-3.4490 -1.1732 0.6023 1.4899 3.0351
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -26.51615 4.94555 -5.362 0.000318 ***
poly(x, 4, raw = TRUE)1 35.82311 3.98204 8.996 4.15e-06 ***
poly(x, 4, raw = TRUE)2 -8.36486 0.96791 -8.642 5.95e-06 ***
poly(x, 4, raw = TRUE)3 0.70812 0.08954 7.908 1.30e-05 ***
poly(x, 4, raw = TRUE)4 -0.01924 0.00278 -6.922 4.08e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.424 on 10 degrees of freedom
Multiple R-squared: 0.9707, Adjusted R-squared: 0.959
F-statistic: 82.92 on 4 and 10 DF, p-value: 1.257e-07
معادلة المنحنى هي كما يلي:
ص = -0.0192×4 + 0.7081×3 – 8.3649×2 + 35.823x – 26.516
يمكننا استخدام هذه المعادلة للتنبؤ بقيمة متغير الاستجابة بناءً على المتغيرات المتوقعة في النموذج. على سبيل المثال، إذا كانت x = 4 فإننا نتوقع أن y = 23.34 :
ص = -0.0192(4) 4 + 0.7081(4) 3 – 8.3649(4) 2 + 35.823(4) – 26.516 = 23.34
مصادر إضافية
مقدمة للانحدار متعدد الحدود
الانحدار متعدد الحدود في R (خطوة بخطوة)
كيفية استخدام الدالة seq في R