كيفية تفسير منحنى roc (مع أمثلة)
الانحدار اللوجستي هو طريقة إحصائية نستخدمها لتناسب نموذج الانحدار عندما يكون متغير الاستجابة ثنائيًا. لتقييم مدى ملاءمة نموذج الانحدار اللوجستي لمجموعة البيانات، يمكننا النظر إلى المقياسين التاليين:
- الحساسية: احتمال أن يتنبأ النموذج بنتيجة إيجابية لملاحظة ما عندما تكون النتيجة إيجابية بالفعل.
- الخصوصية: احتمال أن يتنبأ النموذج بنتيجة سلبية لملاحظة ما عندما تكون النتيجة سلبية بالفعل.
إحدى الطرق البسيطة لتصور هذين المقياسين هي إنشاء منحنى ROC ، وهو رسم بياني يعرض حساسية وخصوصية نموذج الانحدار اللوجستي.
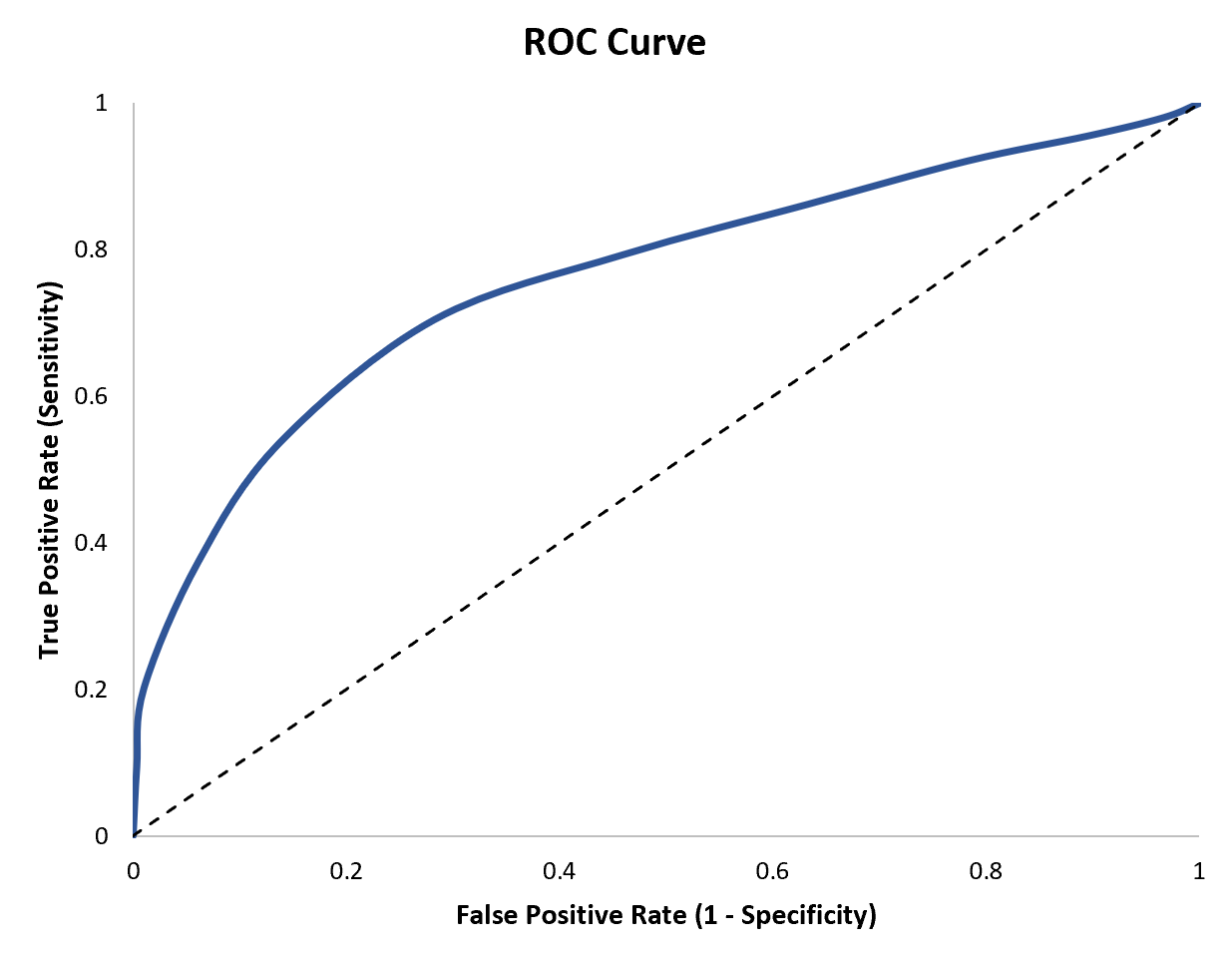
يشرح هذا البرنامج التعليمي كيفية إنشاء وتفسير منحنى ROC.
كيفية إنشاء منحنى ROC
بمجرد الانتهاء من تركيب نموذج الانحدار اللوجستي، يمكننا استخدام النموذج لتصنيف الملاحظات إلى واحدة من فئتين.
على سبيل المثال، يمكننا تصنيف الملاحظات على أنها “إيجابية” أو “سلبية”.
يمثل المعدل الإيجابي الحقيقي نسبة الملاحظات التي يجب أن تكون إيجابية عندما تكون كذلك بالفعل.
وعلى العكس من ذلك، يمثل المعدل الإيجابي الكاذب نسبة الملاحظات التي ينبغي أن تكون إيجابية ولكنها في الواقع سلبية.
عندما نقوم بإنشاء منحنى ROC، فإننا نرسم أزواج المعدل الإيجابي الحقيقي مقابل المعدل الإيجابي الخاطئ لكل عتبة قرار محتملة لنموذج الانحدار اللوجستي.
كيفية تفسير منحنى ROC
كلما اقترب منحنى ROC من الزاوية اليسرى العليا من المخطط، كلما كان النموذج قادرًا على تصنيف البيانات إلى فئات بشكل أفضل.
لتحديد ذلك، يمكننا حساب AUC (المساحة الواقعة تحت المنحنى) والتي تخبرنا بمقدار قطعة الأرض الموجودة تحت المنحنى.
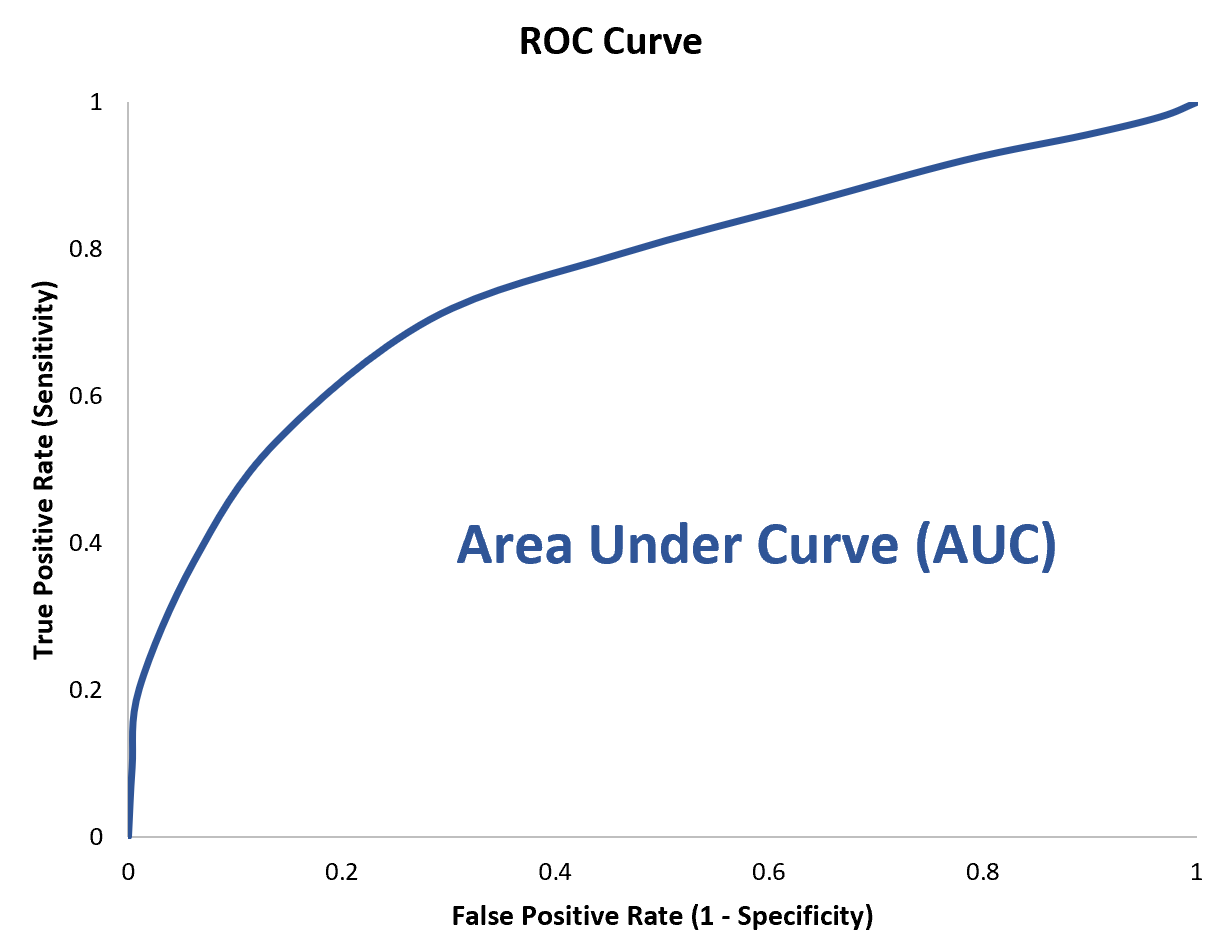
كلما اقتربت AUC من 1، كان النموذج أفضل.
سيكون النموذج ذو المساحة تحت المنحنى (AUC) الذي يساوي 0.5 بمثابة خط قطري مثالي وسيمثل نموذجًا ليس أفضل من النموذج الذي يقوم بتصنيفات عشوائية.
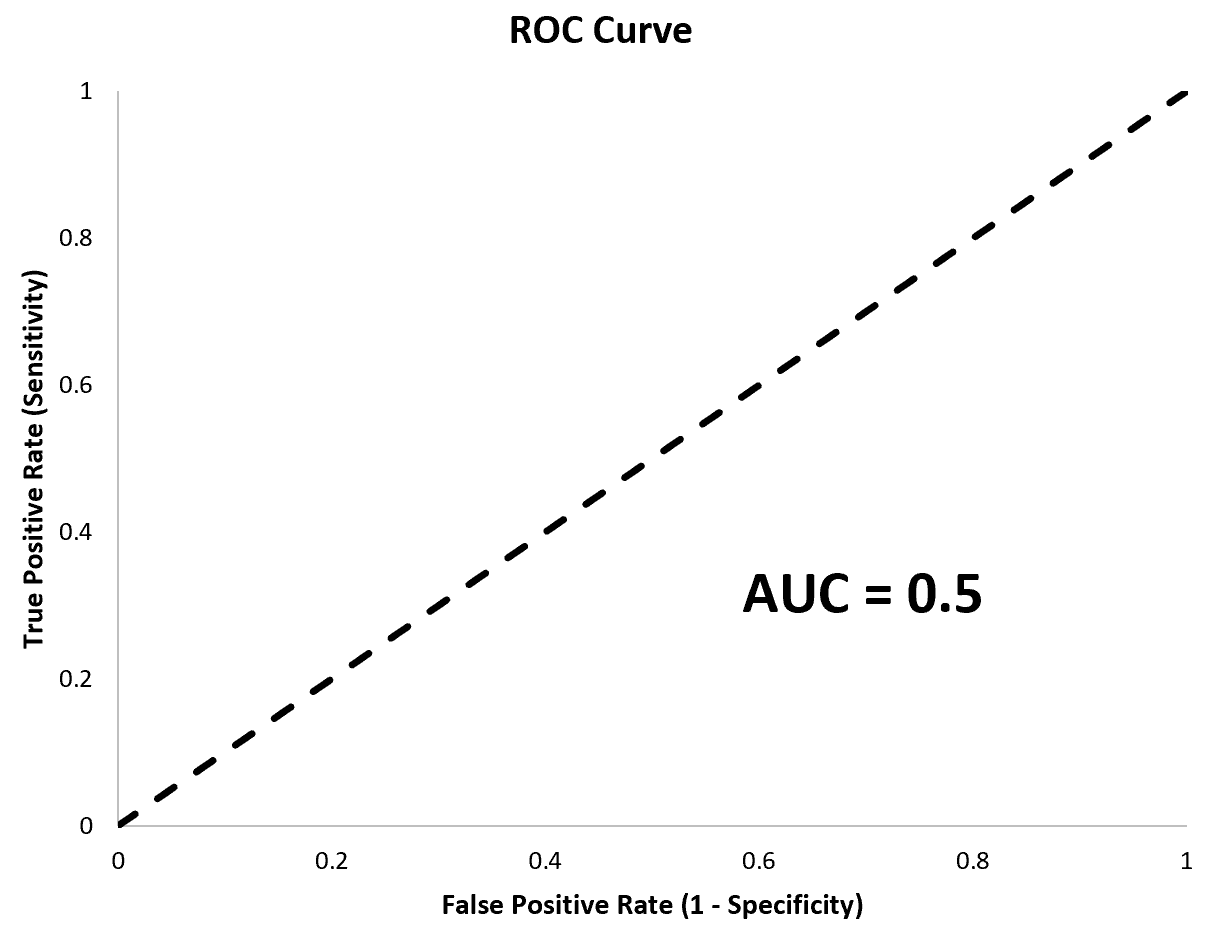
من المفيد بشكل خاص حساب AUC لنماذج الانحدار اللوجستي المتعددة لأنه يسمح لنا بمعرفة النموذج الأفضل في عمل التنبؤات.
على سبيل المثال، لنفترض أننا قمنا بتركيب ثلاثة نماذج مختلفة للانحدار اللوجستي ورسمنا منحنيات ROC التالية لكل نموذج:
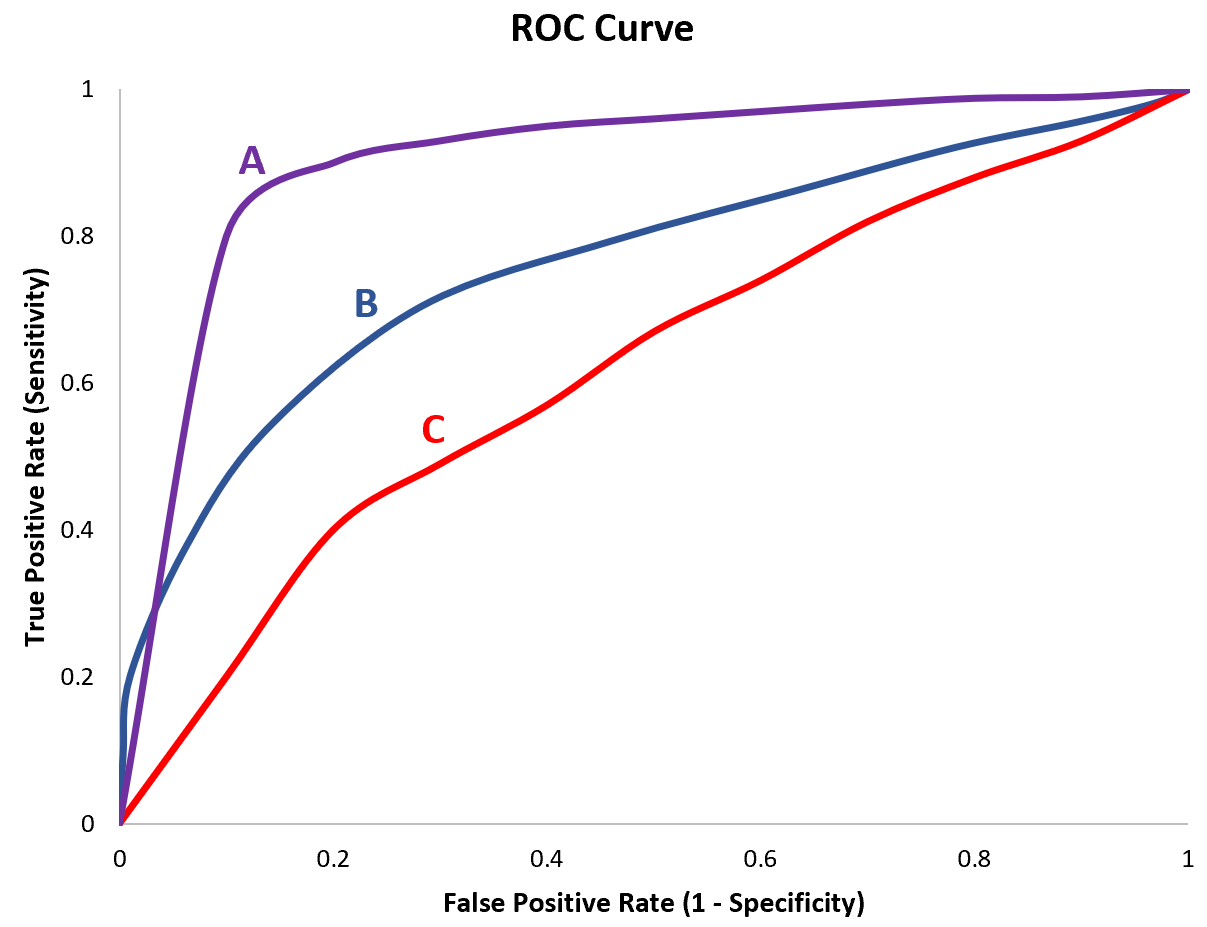
لنفترض أننا نحسب AUC لكل نموذج على النحو التالي:
- النموذج أ: الجامعة الأمريكية بالقاهرة = 0.923
- النموذج ب: الجامعة الأمريكية بالقاهرة = 0.794
- النموذج ج: الجامعة الأمريكية بالقاهرة = 0.588
يحتوي النموذج A على أعلى مساحة تحت المنحنى، مما يشير إلى أنه يحتوي على أعلى منطقة أسفل المنحنى وهو أفضل نموذج لتصنيف الملاحظات بشكل صحيح إلى فئات.
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية إنشاء منحنيات ROC باستخدام برامج إحصائية مختلفة:
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر