كيفية حساب توزيعات العينات في r

توزيع العينات هو توزيع احتمالي لإحصائية معينة بناءً على العديد من العينات العشوائية من مجتمع واحد.

يشرح هذا البرنامج التعليمي كيفية القيام بما يلي مع توزيعات العينات في R:

• إنشاء توزيع العينات.
• تصور توزيع العينات.
• حساب المتوسط والانحراف المعياري لتوزيع العينات.
• احسب الاحتمالات المتعلقة بتوزيع العينات.

إنشاء توزيع العينات في R

يوضح الكود التالي كيفية إنشاء توزيع العينات في R:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

في هذا المثال، استخدمنا الدالة rnorm() لحساب متوسط 10000 عينة كان حجم كل عينة فيها 20 وتم إنشاؤها من توزيع طبيعي بمتوسط 5.3 وانحراف معياري قدره 9.

يمكننا أن نرى أن متوسط العينة الأولى كان 5.283992، وأن متوسط العينة الثانية كان 6.304845، وهكذا.

تصور توزيع العينات

يوضح الكود التالي كيفية إنشاء رسم بياني بسيط لتصور توزيع العينات:

 #create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

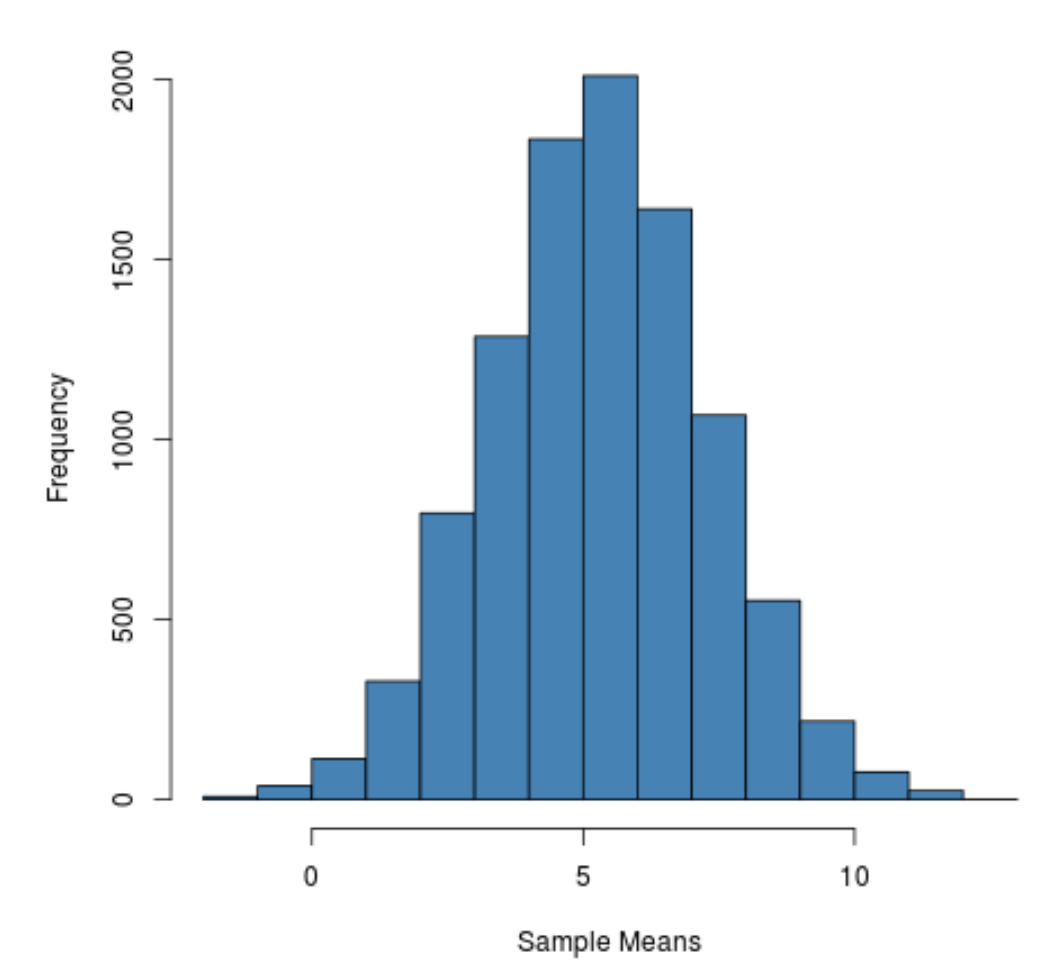
ويمكن ملاحظة أن توزيع العينات على شكل جرس مع ذروة قريبة من القيمة 5.

ومع ذلك، من ذيل التوزيع يمكننا أن نرى أن بعض العينات كان لها متوسط أكبر من 10 والبعض الآخر كان لها متوسط أقل من 0.

أوجد المتوسط والانحراف المعياري

يوضح الكود التالي كيفية حساب المتوسط والانحراف المعياري لتوزيع العينات:

 #mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

ومن الناحية النظرية، ينبغي أن يكون متوسط توزيع العينات 5.3. يمكننا أن نرى أن متوسط العينة الفعلي في هذا المثال هو 5.287195 ، وهو قريب من 5.3.

ومن الناحية النظرية، يجب أن يكون الانحراف المعياري لتوزيع العينات مساوياً لـ s/√n، والذي سيكون 9 / √20 = 2.012. يمكننا أن نرى أن الانحراف المعياري الفعلي لتوزيع العينات هو 2.00224 ، وهو قريب من 2.012.

احسب الاحتمالات

يوضح الكود التالي كيفية حساب احتمالية الحصول على قيمة معينة لمتوسط العينة، بمعلومية متوسط السكان، والانحراف المعياري للسكان، وحجم العينة.

 #calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

في هذا المثال بالذات نجد احتمال أن يكون متوسط العينة أقل من أو يساوي 6، بشرط أن يكون متوسط السكان 5.3، والانحراف المعياري للسكان 9، وحجم العينة 20 هو 0.6417 .

وهذا قريب جدًا من الاحتمالية المحسوبة بواسطة حاسبة توزيع العينات :

الكود الكامل

يظهر أدناه رمز R الكامل المستخدم في هذا المثال:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

مصادر إضافية

مقدمة لتوزيعات العينات
حاسبة توزيع العينات
مقدمة لنظرية الحد المركزي