مقدمة للتوزيع ذي الحدين

التوزيع ذو الحدين هو أحد التوزيعات الأكثر شعبية في الإحصاء. لفهم التوزيع ذي الحدين، من المفيد أن نفهم أولاً التجارب ذات الحدين .

تجارب ذات الحدين

التجربة ذات الحدين هي تجربة لها الخصائص التالية:

• تتكون التجربة من تجارب متكررة.
• كل تجربة لها نتيجتين محتملتين فقط.
• احتمال النجاح، المشار إليه بـ p ، هو نفسه لكل تجربة.
• كل اختبار مستقل.

المثال الأكثر وضوحًا للتجربة ذات الحدين هو رمي العملة المعدنية. على سبيل المثال، لنفترض أننا نقلب عملة معدنية 10 مرات. هذه تجربة ذات الحدين لأنها تحتوي على الخصائص الأربع التالية:

• تتكون التجربة من تجارب متكررة – هناك 10 تجارب.
• كل تجربة لها نتيجتان محتملتان فقط: الرأس أو الذيل.
• احتمال النجاح، المشار إليه بـ p ، هو نفسه لكل تجربة. إذا عرفنا “النجاح” بأنه رؤوس الهبوط، فإن احتمال النجاح هو بالضبط 0.5 لكل تجربة.
• كل تجربة مستقلة – نتيجة رمية عملة واحدة لا تؤثر على نتيجة أي رمية عملة أخرى.

التوزيع ذو الحدين

يصف التوزيع ذو الحدين احتمالية الحصول على نجاحات k في تجارب ذات الحدين.

إذا كان المتغير العشوائي X يتبع التوزيع ذي الحدين، فيمكن العثور على احتمال نجاح X = k من خلال الصيغة التالية:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ذهب:

• ن: عدد التجارب
• ك: عدد النجاحات
• ع: احتمال النجاح في تجربة معينة
• _n C _k : عدد الطرق للحصول على نجاحات k في التجارب n

على سبيل المثال، لنفترض أننا نقلب عملة معدنية 3 مرات. يمكننا استخدام الصيغة أعلاه لتحديد احتمالية الحصول على 0 و1 و2 و3 رؤوس في هذه الرميات الثلاث:

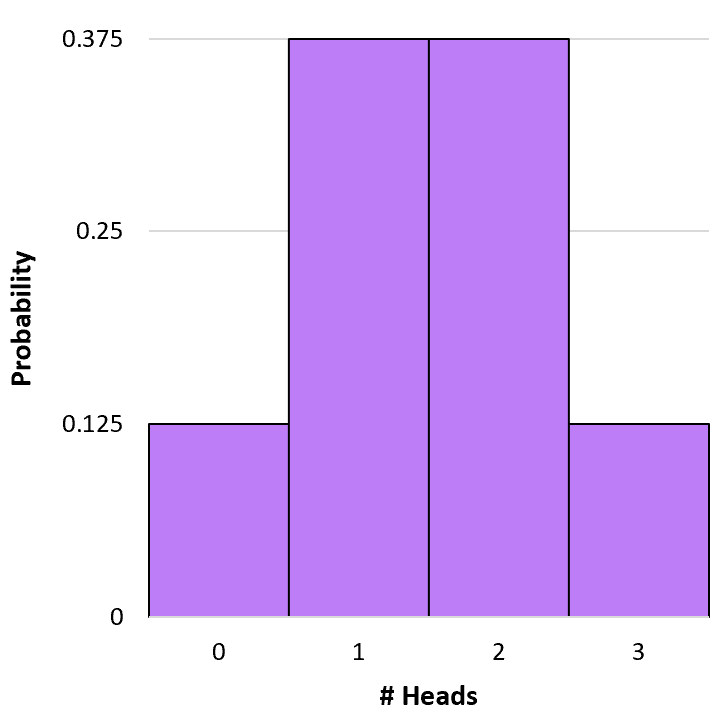
ف(X=0) = ₃ ج ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125

ف(X=1) = ₃ ج ₁ * 0.5 ¹ * (1-0.5) ^3-1 = 3 * 0.5 * (0.5) ² = 0.375

ف(X=2) = ₃ ج ₂ * 0.5 ² * (1-0.5) ^3-2 = 3 * 0.25 * (0.5) ¹ = 0.375

ف(X=3) = ₃ ج ₃ * 0.5 ³ * (1-0.5) ^3-3 = 1 * 0.125 * (0.5) ⁰ = 0.125

ملاحظة : استخدمنا هذه الآلة الحاسبة المدمجة لحساب _{nCk لكل} مثال.

يمكننا إنشاء رسم بياني بسيط لتصور هذا التوزيع الاحتمالي:

حساب الاحتمالات ذات الحدين التراكمية

من السهل حساب احتمالية ذات حدين واحدة (على سبيل المثال احتمال ظهور عملة معدنية مرة واحدة من أصل 3 رميات) باستخدام الصيغة أعلاه، ولكن لحساب الاحتمالات التراكمية ذات الحدين نحتاج إلى إضافة احتمالات فردية.

على سبيل المثال، لنفترض أننا نريد معرفة احتمالية ظهور العملة المعدنية مرة واحدة أو أقل من أصل 3 رميات. سوف نستخدم الصيغة التالية لحساب هذا الاحتمال:

P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 .

وهذا ما يسمى بالاحتمال التراكمي لأنه يتضمن إضافة احتمالات متعددة. يمكننا حساب الاحتمال التراكمي للحصول على عدد k أو أقل لكل نتيجة باستخدام صيغة مماثلة:

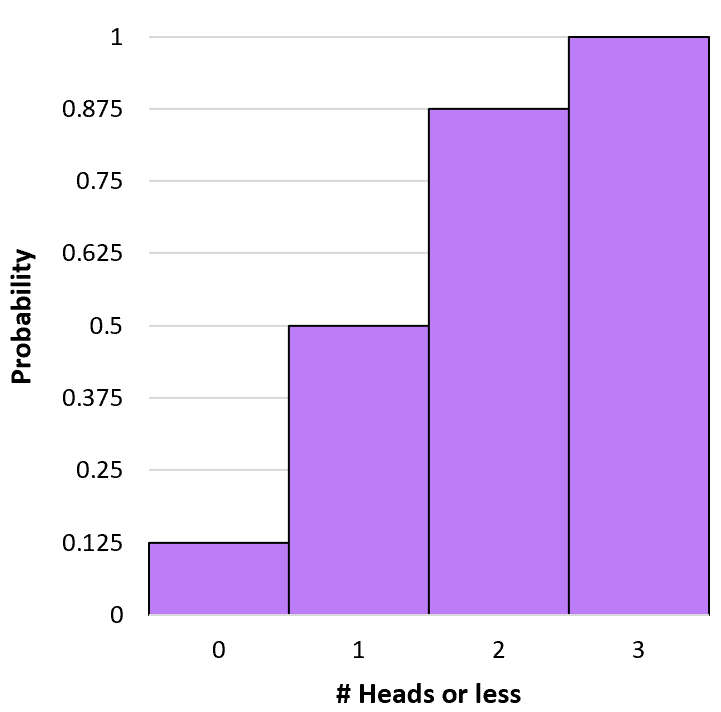
ف(X≥0) = ف(X=0) = 0.125 .

P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 .

P(X≥2) = P(X=0) + P(X=1) + P(X=2) = 0.125 + 0.375 + 0.375 = 0.875 .

P(X≥3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0.125 + 0.375 + 0.375 + 0.125 = 1 .

يمكننا إنشاء رسم بياني لتصور هذا التوزيع الاحتمالي التراكمي:

حاسبة الاحتمالية ذات الحدين

عندما نعمل مع أعداد صغيرة (على سبيل المثال، رمي العملات المعدنية ثلاث مرات)، فمن المعقول حساب احتمالات ذات الحدين يدويًا. ومع ذلك، عندما نعمل بأعداد أكبر (على سبيل المثال، 100 سحب)، قد يكون من الصعب حساب الاحتمالات يدويًا. في هذه الحالات، قد يكون من المفيد استخدام حاسبة الاحتمالية ذات الحدين مثل تلك الموجودة أدناه.

على سبيل المثال، لنفترض أننا رمينا عملة معدنية n = 100 مرة، فإن احتمال سقوطها على الصور في تجربة معينة هو p = 0.5، ونريد أن نعرف احتمال سقوطها على الصور k = 43 مرة أو أقل:

وإليك كيفية تفسير النتيجة:

• احتمال ظهور العملة على الوجه 43 مرة بالضبط هو 0.03007 .
• احتمال ظهور العملة على الوجه أقل من 43 مرة هو 0.06661 .
• احتمال ظهور العملة على الوجه 43 مرة أو أقل هو 0.09667 .
• احتمال ظهور العملة على الوجه أكثر من 43 مرة هو 0.90333 .
• احتمال ظهور العملة على الوجه 43 مرة أو أكثر هو 0.93339 .

خصائص التوزيع ذي الحدين

التوزيع ذو الحدين له الخصائص التالية:

متوسط التوزيع هو μ = np

تباين التوزيع هو σ ² = np(1-p)

الانحراف المعياري للتوزيع هو σ = √ np(1-p)

على سبيل المثال، لنفترض أننا ألقينا قطعة نقود 3 مرات. دع p = احتمال سقوط العملة على الرؤوس.

متوسط عدد الرؤوس التي نتوقعها هو μ = np = 3*.5 = 1.5 .

تباين عدد الرأس الذي نتوقعه هو σ ² = np(1-p) = 3*.5*(1-.5) = 0.75 .

مشاكل ممارسة التوزيع ذي الحدين

استخدم المسائل التدريبية التالية لاختبار معرفتك بالتوزيع ذي الحدين.

المشكلة 1

سؤال: يقوم بوب بنسبة 60% من محاولات الرمية الحرة. إذا نفذ 12 رمية حرة، فما احتمال أن ينفذ 10 رميات بالضبط؟

الإجابة: باستخدام حاسبة التوزيع ذات الحدين أعلاه حيث p = 0.6 و n = 12 و k = 10، نجد أن P(X=10) = 0.06385 .

المشكلة 2

السؤال: تقلب جيسيكا العملة المعدنية 5 مرات. ما هو احتمال ظهور العملة على الوجه مرتين أو أقل؟

الإجابة: باستخدام حاسبة التوزيع ذات الحدين أعلاه حيث p = 0.5 و n = 5 و k = 2، نجد أن P(X≥2) = 0.5 .

المشكلة 3

سؤال: احتمال قبول طالب معين في كلية معينة هو 0.2. إذا تقدم 10 طلاب، ما هو احتمال قبول أكثر من 4 طلاب؟

الإجابة: باستخدام حاسبة التوزيع ذات الحدين أعلاه مع p = 0.2 و n = 10 و k = 4، نجد أن P(X>4) = 0.03279 .

المشكلة 4

سؤال: قمت بقلب العملة المعدنية 12 مرة. ما هو متوسط عدد الرؤوس المتوقع ظهورها؟

الإجابة: تذكر أن متوسط التوزيع ذي الحدين يتم حسابه على أنه μ = np. إذن μ = 12*0.5 = 6 رؤوس .

المشكلة 5

سؤال: نجح مارك في تحقيق 10% من محاولاته. إذا نجح في تحقيق خمس محاولات في مباراة معينة، فما التباين في عدد الضربات التي حققها على أرض الملعب؟

الإجابة: تذكر أن تباين التوزيع ذي الحدين يتم حسابه على النحو التالي: σ ² = np(1-p). وبالتالي، ^σ2 = 6*.1*(1-.1) = 0.54 .

مصادر إضافية

يمكن أن تساعدك المقالات التالية في تعلم كيفية استخدام التوزيع ذي الحدين في برامج إحصائية مختلفة:

• كيفية حساب الاحتمالات ذات الحدين في إكسيل
• كيفية حساب الاحتمالات ذات الحدين على الآلة الحاسبة TI-84
• كيفية حساب الاحتمالات ذات الحدين في R
• كيفية رسم التوزيع ذي الحدين في R