التوزيع السلبي ذو الحدين

By دكتور بنيامين أندرسون زومار 3, 2023 احتمالا 0 Comments

تشرح هذه المقالة ما هو التوزيع السالب ذو الحدين وفيم يتم استخدامه. ستجد أيضًا صيغة التوزيع السلبي ذي الحدين، ومثالًا ملموسًا وخصائص هذا النوع من التوزيع الاحتمالي. وأخيرًا، ستتمكن من حساب أي احتمال توزيع سلبي ذي الحدين باستخدام الآلة الحاسبة عبر الإنترنت.

ما هو التوزيع السلبي ذو الحدين؟

التوزيع السلبي ذو الحدين هو توزيع احتمالي يصف عدد تجارب برنولي المطلوبة للحصول على عدد معين من النتائج الإيجابية.

ولذلك، فإن التوزيع السلبي ذي الحدين له معلمتان مميزتان: r هو عدد النتائج الناجحة المطلوبة و p هو احتمال النجاح لكل تجربة بيرنولي يتم إجراؤها.

$X\sim \text{BN}(r,p)$

تذكر أن اختبار برنولي هو تجربة لها نتيجتان محتملتان: “النجاح” و”الفشل”. لذا، إذا كان احتمال “النجاح” هو p ، فإن احتمال “الفشل” هو q=1-p .

وبالتالي، فإن التوزيع السلبي ذو الحدين يحدد العملية التي يتم فيها إجراء العديد من تجارب برنولي حسب الضرورة للحصول على نتائج إيجابية. علاوة على ذلك، فإن جميع تجارب برنولي هذه مستقلة ولها احتمالية ثابتة للنجاح .

على سبيل المثال، المتغير العشوائي الذي يتبع التوزيع السالب ذو الحدين هو عدد المرات التي يجب فيها رمي حجر النرد حتى يتم رمي الرقم 6 ثلاث مرات.

الفرق بين التوزيع السالب ذو الحدين والتوزيع ذو الحدين هو أن التوزيع السالب ذو الحدين يحسب عدد المرات التي يستغرقها الحصول على عدد معين من النتائج الناجحة، بينما يحسب التوزيع ذو الحدين عدد الحالات الناجحة في سلسلة اختبارات برنولي.

➤ انظر: ما هو التوزيع ذو الحدين؟

صيغة التوزيع ذات الحدين السلبية

بالنظر إلى المعلمات r، p، x، يتم حساب احتمال التوزيع السلبي ذي الحدين عن طريق ضرب العدد التوافقي لـ x-1 في xr بواسطة (1-p) ^xr بواسطة p ^r .

لذا، فإن صيغة حساب احتمال التوزيع السلبي ذي الحدين هي:

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب احتمال وجود متغير يتبع التوزيع السلبي ذي الحدين.

حل تمرين التوزيع السالب ذو الحدين

ما هو احتمال أنك إذا رميت قطعة نقود ثماني مرات، فسوف تظهر صورة للمرة الرابعة في الرمية الثامنة؟

أولًا، علينا حساب احتمال ظهور الصورة عند رمي قطعة نقود. في هذه الحالة، لدينا نتيجة إيجابية واحدة فقط (الرؤوس) من أصل نتيجتين محتملتين (الرؤوس والذيول)، وبالتالي فإن احتمال النجاح هو:

$p=\cfrac{1}{2}=0,5$

وبالتالي، فإن المتغير العشوائي في هذه المشكلة يتبع توزيعًا سلبيًا ذا الحدين حيث r=4 وp=0.5. لذلك، نستخدم صيغة التوزيع السالبة ذات الحدين لحساب الاحتمال الذي يطلب منا التمرين القيام به.

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

خصائص التوزيع السلبي ذو الحدين

فيما يلي أهم خصائص التوزيع السلبي ذي الحدين.

يتم تعريف التوزيع السلبي ذي الحدين بمعلمتين مميزتين: r هو عدد النتائج الناجحة المرغوبة و p هو احتمال النجاح لكل تجربة بيرنولي يتم إجراؤها.

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

تباين التوزيع السلبي ذو الحدين يساوي r مضروبًا في (1-p) مقسومًا على p ² .

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

إذا كانت المعلمة r أكبر من 1، فيمكن حساب نمط التوزيع السلبي ذي الحدين باستخدام الصيغة التالية:

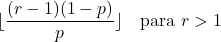
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”221″ style=”vertical-align: -16px;”></p> </p> <ul style=$

دالة الكتلة التي تجعل من الممكن تحديد احتمال التوزيع السلبي ذي الحدين هي كما يلي:

$P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

يتم حساب معامل الانحراف للتوزيع السلبي ذي الحدين بالتعبير التالي:

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

يمكن العثور على التفرطح للتوزيع السلبي ذي الحدين بالصيغة التالية:

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

إذا كانت المعلمة r تساوي 1، فلدينا حالة توزيع هندسي .

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

حاسبة التوزيع ذات الحدين السالبة

أدخل قيم المعلمات r، p، x في الآلة الحاسبة التالية لحساب الاحتمال. يجب عليك إدخال الأرقام باستخدام النقطة كفاصل عشري، على سبيل المثال 0.50.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر