كيفية حساب خطأ الجذر التربيعي (rmse) في excel

في الإحصاء، تحليل الانحدار هو أسلوب نستخدمه لفهم العلاقة بين متغير التوقع، x، ومتغير الاستجابة، y.

عندما نقوم بإجراء تحليل الانحدار، نحصل على نموذج يخبرنا بالقيمة المتوقعة لمتغير الاستجابة بناءً على قيمة المتغير المتنبئ.

إحدى طرق تقييم مدى ملاءمة نموذجنا لمجموعة بيانات معينة هي حساب متوسط الخطأ التربيعي ، وهو مقياس يخبرنا بمدى بعد القيم المتوقعة عن القيم المرصودة لدينا، في المتوسط.

صيغة العثور على متوسط مربع الخطأ، والمعروفة أكثر باسم RMSE ، هي:

RMSE = √[ Σ(P _i – O _i ) ² / n ]

ذهب:

• Σ هو رمز خيالي يعني “المجموع”
• P _i هي القيمة المتوقعة للملاحظة ⁱ في مجموعة البيانات
• O _i هي القيمة المرصودة للملاحظة ^رقم في مجموعة البيانات
• n هو حجم العينة

ملاحظات فنية :

• يمكن حساب متوسط مربع الخطأ لأي نوع من النماذج التي تنتج قيمًا متوقعة، والتي يمكن بعد ذلك مقارنتها بالقيم المرصودة لمجموعة البيانات.
• ويسمى أحيانًا متوسط خطأ المربع أيضًا متوسط انحراف المربع، والذي غالبًا ما يتم اختصاره بـ RMSD.

بعد ذلك، دعونا نلقي نظرة على مثال لكيفية حساب متوسط مربع الخطأ في إكسيل.

كيفية حساب متوسط الخطأ المربع في إكسل

لا توجد وظيفة مدمجة لحساب RMSE في Excel، ولكن يمكننا حسابها بسهولة تامة باستخدام صيغة واحدة. سنوضح كيفية حساب RMSE لسيناريوهين مختلفين.

السيناريو 1

في السيناريو، يمكن أن يكون لديك عمود واحد يحتوي على القيم المتوقعة من النموذج الخاص بك وعمود آخر يحتوي على القيم المرصودة. توضح الصورة أدناه مثالاً على هذا السيناريو:

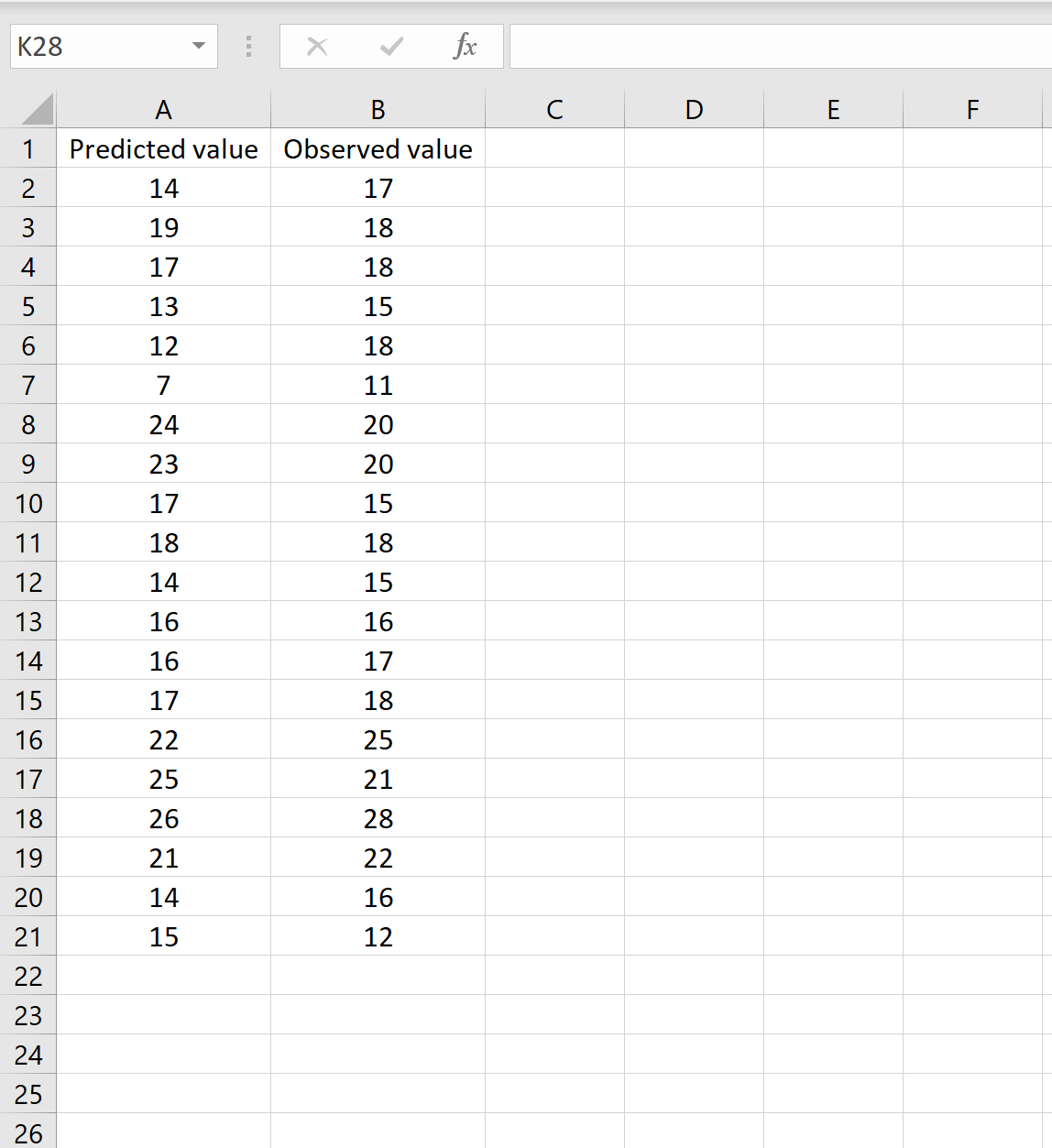
إذا كان الأمر كذلك، فيمكنك حساب RMSE عن طريق كتابة الصيغة التالية في أي خلية ثم النقر فوق CTRL+SHIFT+ENTER:

=SQRT(SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21))

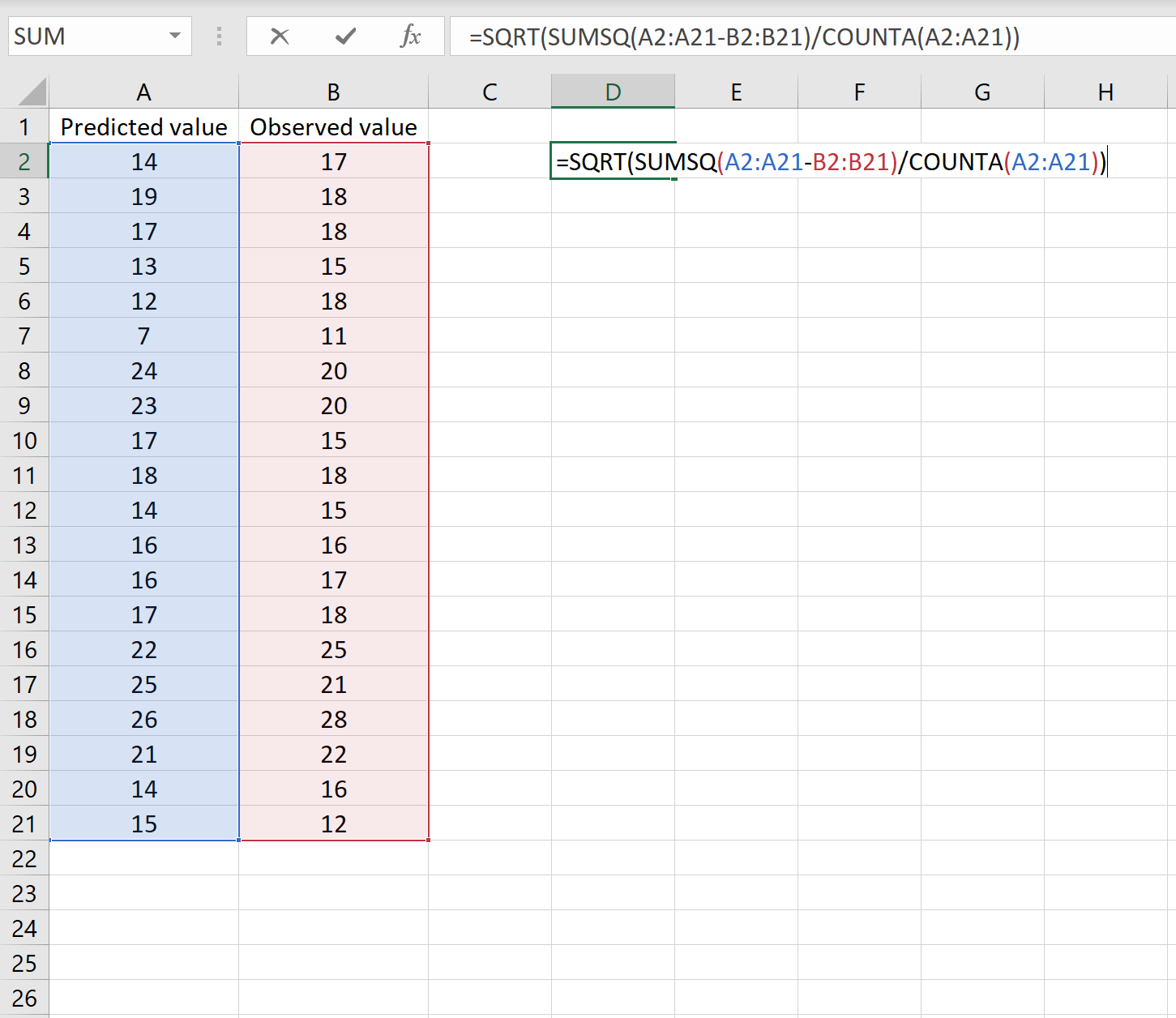
هذا يخبرنا أن متوسط مربع الخطأ هو 2.6646 .

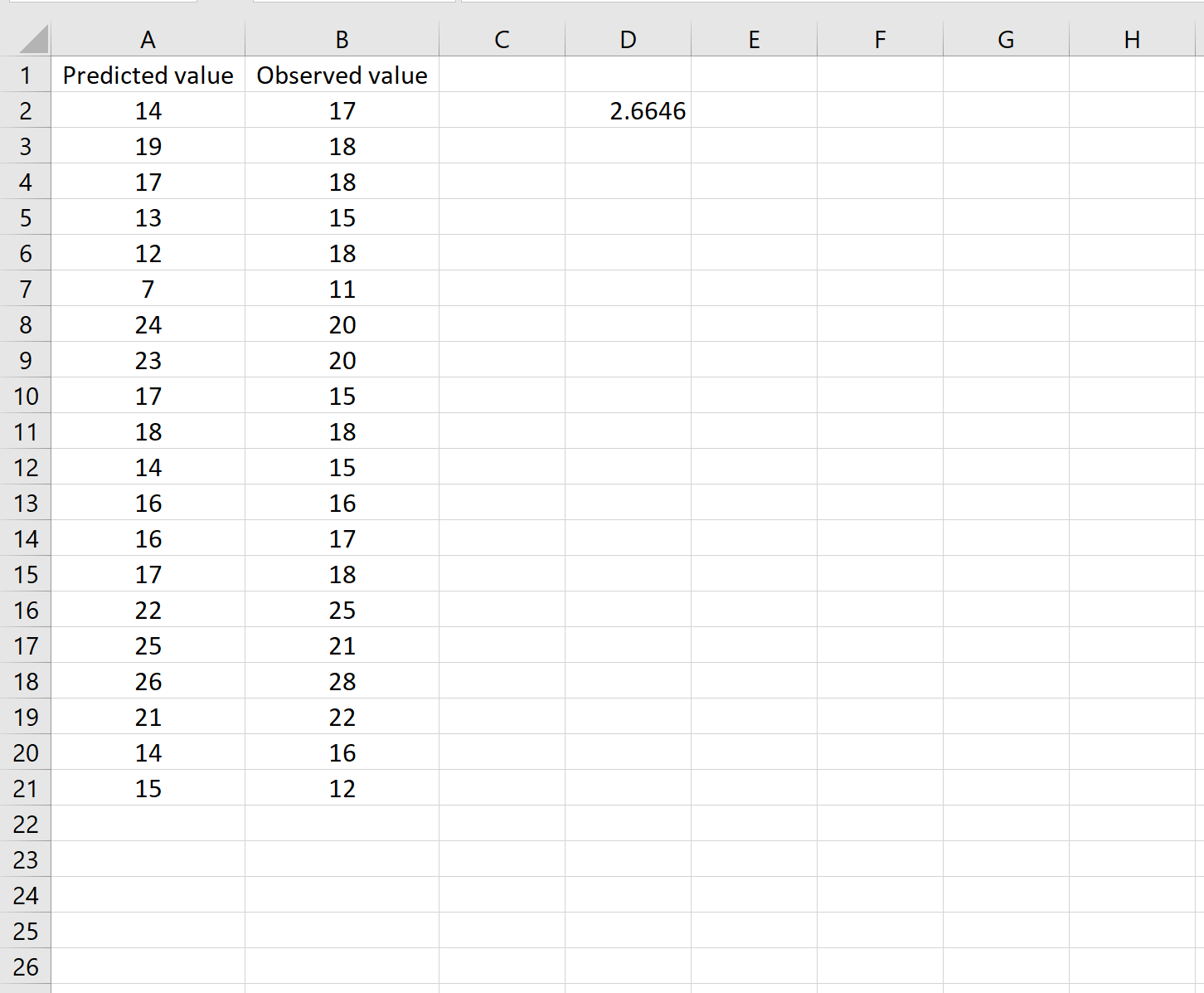
قد تبدو الصيغة صعبة بعض الشيء، لكنها تصبح منطقية بمجرد تحليلها:

= SQRT( SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21) )

• أولاً، نحسب مجموع مربعات الاختلافات بين القيم المتوقعة والمرصودة باستخدام الدالة SUMSQ() .
• بعد ذلك، نقسم على حجم عينة مجموعة البيانات باستخدام COUNTA() ، الذي يحسب عدد الخلايا غير الفارغة في النطاق.
• وأخيرًا، نأخذ الجذر التربيعي للعملية الحسابية بأكملها باستخدام الدالة SQRT() .

السيناريو 2

في سيناريو آخر، ربما تكون قد قمت بالفعل بحساب الاختلافات بين القيم المتوقعة والقيم المرصودة. في هذه الحالة سيكون لديك عمود واحد فقط يوضح الاختلافات.

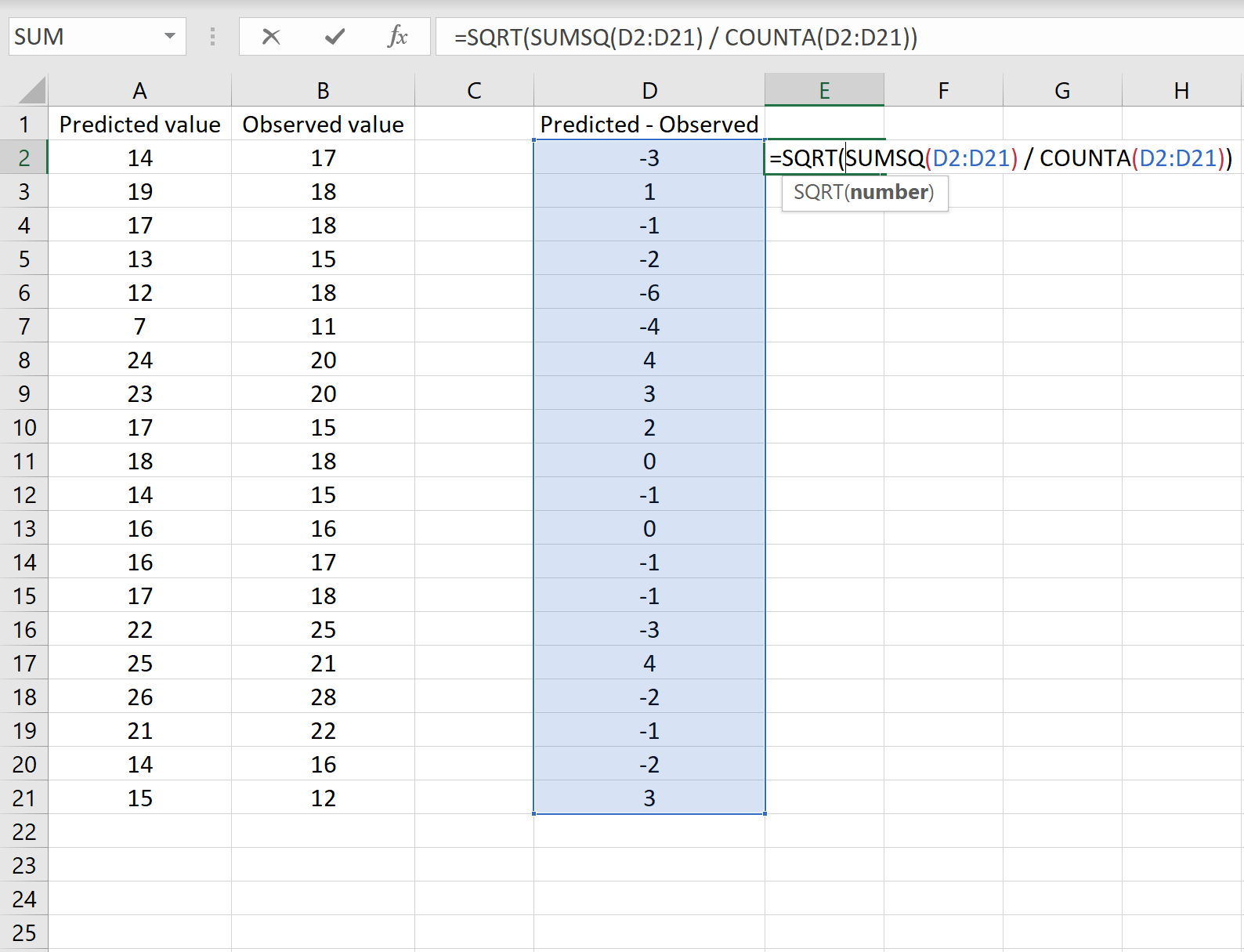
توضح الصورة أدناه مثالاً على هذا السيناريو. تظهر القيم المتوقعة في العمود أ، والقيم المرصودة في العمود ب، والفرق بين القيم المتوقعة والمرصودة في العمود د:

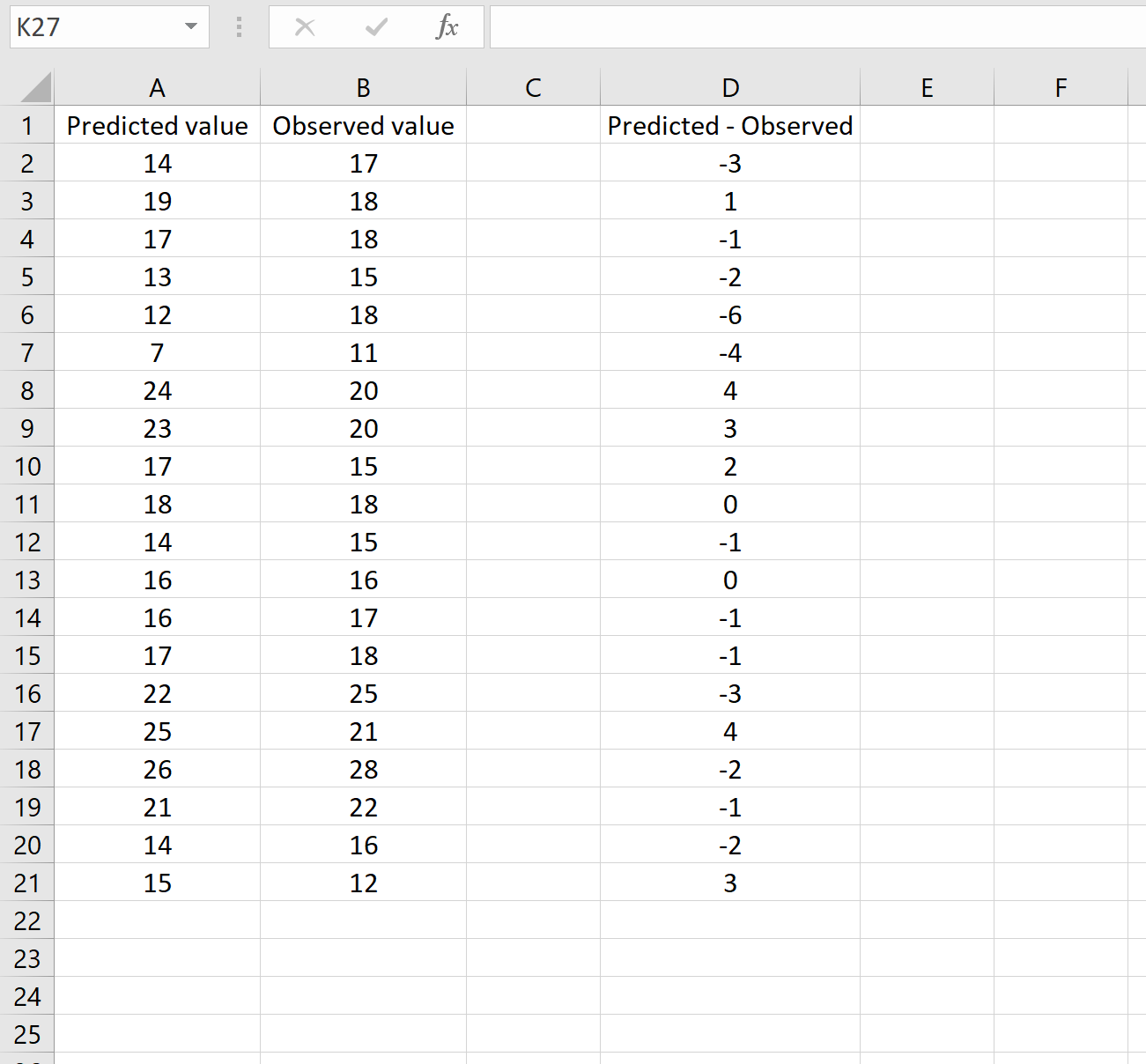
إذا كان الأمر كذلك، فيمكنك حساب RMSE عن طريق كتابة الصيغة التالية في أي خلية ثم النقر فوق CTRL+SHIFT+ENTER:

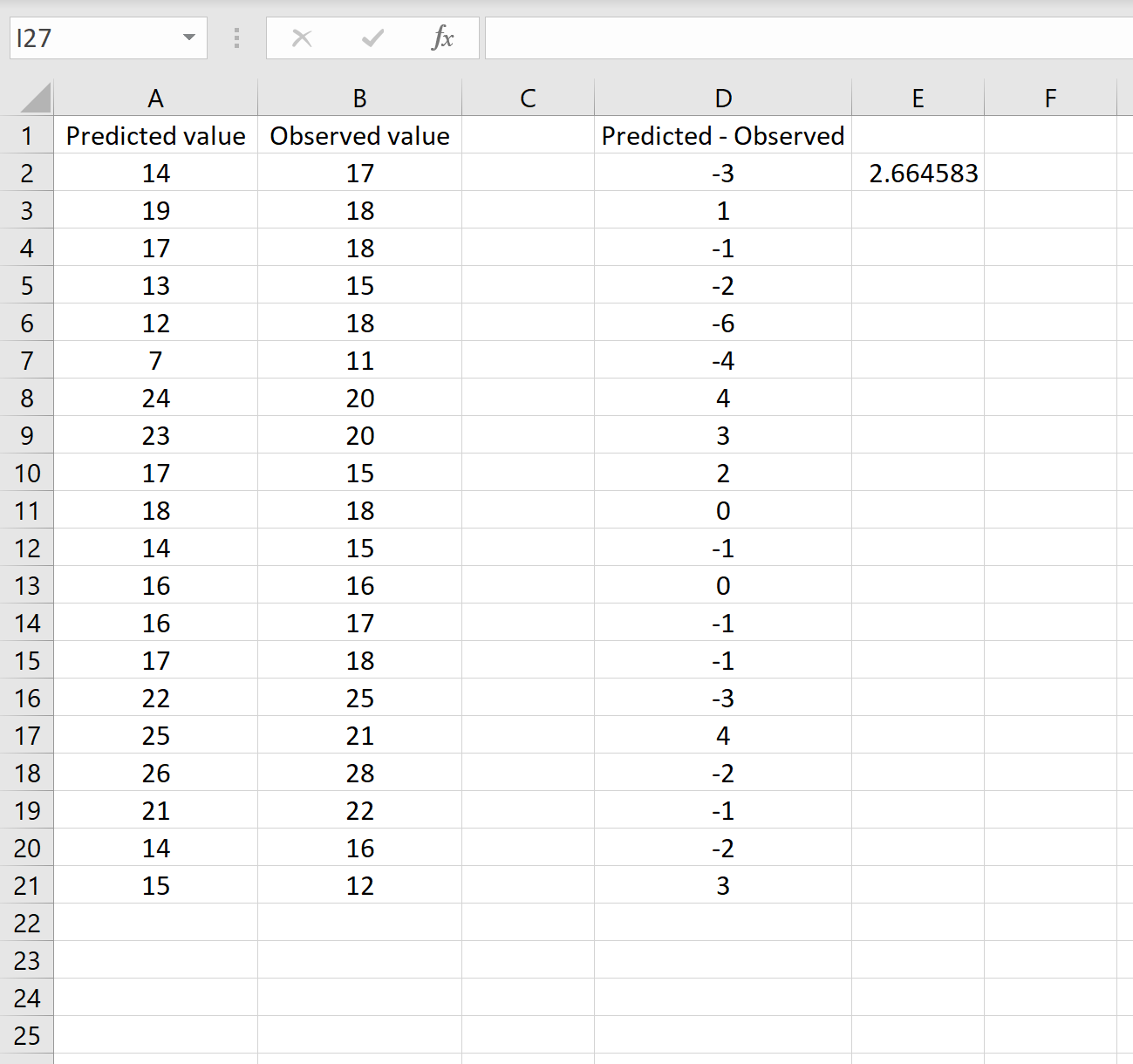
=SQRT(SUMSQ(D2:D21) / COUNT(D2:D21))

يخبرنا هذا أن متوسط مربع الخطأ هو 2.6646 ، وهو ما يتوافق مع النتيجة التي تم الحصول عليها في السيناريو الأول. وهذا يؤكد أن هذين النهجين لحساب RMSE متساويان.

تختلف الصيغة التي استخدمناها في هذا السيناريو قليلاً عما استخدمناه في السيناريو السابق:

= SQRT( SUMSQ(D2:D21) / COUNT(D2:D21) )

• وبما أننا قمنا بالفعل بحساب الاختلافات بين القيم المتوقعة والمرصودة في العمود D، فيمكننا حساب مجموع الفروق المربعة باستخدام الدالة SUMSQ().   الدالة مع القيم من العمود D فقط.
• بعد ذلك، نقسم على حجم عينة مجموعة البيانات باستخدام COUNTA() ، الذي يحسب عدد الخلايا غير الفارغة في النطاق.
• وأخيرًا، نأخذ الجذر التربيعي للعملية الحسابية بأكملها باستخدام الدالة SQRT() .

كيفية تفسير RMSE

كما ذكرنا سابقًا، تعد RMSE طريقة مفيدة لمعرفة مدى قدرة نموذج الانحدار (أو أي نموذج ينتج قيمًا متوقعة) على “ملاءمة” مجموعة البيانات.

كلما زاد حجم RMSE، زاد الفرق بين القيم المتوقعة والمرصودة، مما يعني أنه كلما كان نموذج الانحدار مناسبًا للبيانات. على العكس من ذلك، كلما كان RMSE أصغر، كلما كانت قدرة النموذج على ملاءمة البيانات أفضل.

قد يكون من المفيد بشكل خاص مقارنة RMSE لنموذجين مختلفين لمعرفة النموذج الذي يناسب البيانات بشكل أفضل.

لمزيد من البرامج التعليمية في Excel، تأكد من مراجعة صفحة أدلة Excel الخاصة بنا، والتي تسرد جميع برامج Excel التعليمية حول الإحصائيات.