فهم اختبار t في الانحدار الخطي

يستخدم الانحدار الخطي لتحديد العلاقة بين متغير التوقع ومتغير الاستجابة.

عندما نقوم بإجراء الانحدار الخطي، نريد أن نعرف ما إذا كانت هناك علاقة ذات دلالة إحصائية بين متغير التوقع ومتغير الاستجابة.

نحن نختبر الأهمية من خلال إجراء اختبار t لمنحدر الانحدار. نستخدم الفرضية الصفرية والبديلة التالية لاختبار t:

• H ₀ : β ₁ = 0 (الميل يساوي صفر)
• H _A : β ₁ ≠ 0 (الميل لا يساوي الصفر)

ثم نقوم بحساب إحصائية الاختبار على النحو التالي:

ر = ب / SE _ب

ذهب:

• ب : تقدير المعامل
• SE _b : الخطأ المعياري في تقدير المعامل

إذا كانت القيمة p التي تقابل t أقل من عتبة معينة (على سبيل المثال α = 0.05)، فإننا نرفض فرضية العدم ونستنتج أن هناك علاقة ذات دلالة إحصائية بين متغير التوقع ومتغير الاستجابة.

يوضح المثال التالي كيفية إجراء اختبار t لنموذج الانحدار الخطي عمليًا.

مثال: إجراء اختبار t للانحدار الخطي

لنفترض أن الأستاذ يريد تحليل العلاقة بين ساعات الدراسة ودرجات الامتحان لـ 40 من طلابه.

وهو ينفذ انحدارًا خطيًا بسيطًا باستخدام الساعات التي تمت دراستها كمتغير متوقع ودرجات الامتحانات المستلمة كمتغير الاستجابة.

ويبين الجدول التالي نتائج نموذج الانحدار:

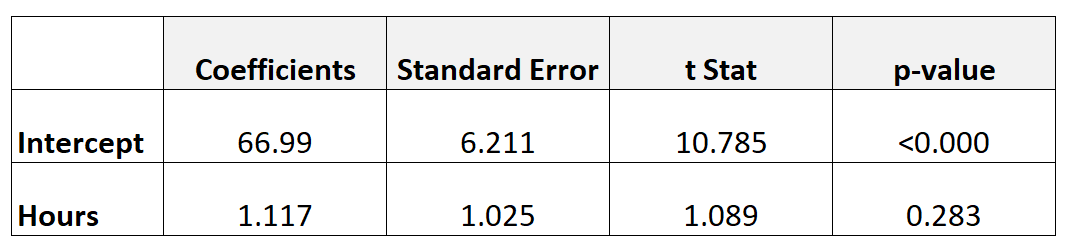
لتحديد ما إذا كانت ساعات الدراسة لها علاقة ذات دلالة إحصائية مع درجة الامتحان النهائي، يمكننا إجراء اختبار t.

نستخدم الفرضية الصفرية والبديلة التالية لاختبار t:

• H ₀ : β ₁ = 0 (ميل الساعات المدروسة يساوي صفر)
• H _A : β ₁ ≠ 0 (ميل الساعات المدروسة لا يساوي الصفر)

ثم نقوم بحساب إحصائية الاختبار على النحو التالي:

• ر = ب / SE _ب
• ر = 1.117 / 1.025
• ر = 1.089

القيمة p التي تتوافق مع t = 1.089 مع df = n-2 = 40 – 2 = 38 هي 0.283 .

لاحظ أنه يمكننا أيضًا استخدام حاسبة القيمة P من نقاط T لحساب قيمة p هذه:

وبما أن هذه القيمة p لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم.

وهذا يعني أن ساعات الدراسة ليس لها علاقة ذات دلالة إحصائية بين نتائج الامتحان النهائي.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول الانحدار الخطي:

مقدمة إلى الانحدار الخطي البسيط
مقدمة في الانحدار الخطي المتعدد
كيفية تفسير معاملات الانحدار
كيفية تفسير اختبار F للأهمية الشاملة في الانحدار