أحداث شاملة أو متنافية

حدثان متنافيان إذا لم يمكن أن يحدثا في نفس الوقت.

على سبيل المثال، لنفترض أن الحدث A هو حدث سقوط حجر النرد على رقم زوجي، والحدث B هو حدث سقوط حجر النرد على رقم فردي.

ويمكننا تعريف فضاء العينة للأحداث على النحو التالي:

• أ = {2، 4، 6}
• ب = {1، 3، 5}

لاحظ أنه لا يوجد تداخل بين المساحتين اللتين تم أخذ عينات منهما. لذا فإن الحدثين A وB متنافيان لأنه لا يمكن أن يحدثا معًا في نفس الوقت. الرقم الذي يقع عليه حجر النرد لا يمكن أن يكون زوجيًا وفرديًا .

وعلى العكس من ذلك، يكون الحدثان شاملين لبعضهما البعض إذا أمكن حدوثهما في نفس الوقت.

على سبيل المثال، ليكن الحدث C هو الحدث الذي يقع فيه حجر النرد على رقم زوجي، وليكن الحدث D هو الحدث الذي يقع فيه حجر النرد على رقم أكبر من 3.

ويمكننا تعريف فضاء العينة للأحداث على النحو التالي:

• ج = {2، 4، 6}
• د = {4، 5، 6}

لاحظ أن هناك تداخلًا بين المساحتين اللتين تم أخذ عينات منهما. وبالتالي، فإن الحدثين C وD كلاهما شاملان لبعضهما البعض لأنهما يمكن أن يحدثا في نفس الوقت. من الممكن أن يستقر النرد على رقم زوجي أكبر من 3.

احتمالات الحدث

إذا كان هناك حدثان متنافيان ، فإن احتمال وقوعهما يساوي صفرًا.

على سبيل المثال، ضع في اعتبارك مثالين للحدثين A وB أعلاه:

• أ = {2، 4، 6}
• ب = {1، 3، 5}

وبما أنه لا يوجد تداخل في فضاءات العينة، فإننا نقول P(A and B) = 0 .

لكن إذا كان هناك حدثان متكاملان ، فإن احتمال وقوعهما معًا سيكون عددًا أكبر من الصفر.

على سبيل المثال، خذ بعين الاعتبار مثالين للحدثين C وD سابقًا:

• ج = {2، 4، 6}
• د = {4، 5، 6}

نظرًا لوجود 6 أرقام محتملة يمكن أن يستقر عليها النرد واثنان من هذه الأرقام (4 و 6) ينتميان إلى كلا الحدثين C و D، فسنحسب P(C و D) كـ 2/6 أو 1/3 .

عرض الأحداث الشاملة والحصرية للطرفين

غالبًا ما نستخدم مخططات فين لتصور الاحتمالات المرتبطة بالأحداث.

إذا كان هناك حدثان متنافيان ، فلن يتداخلا على الإطلاق في مخطط Venn:

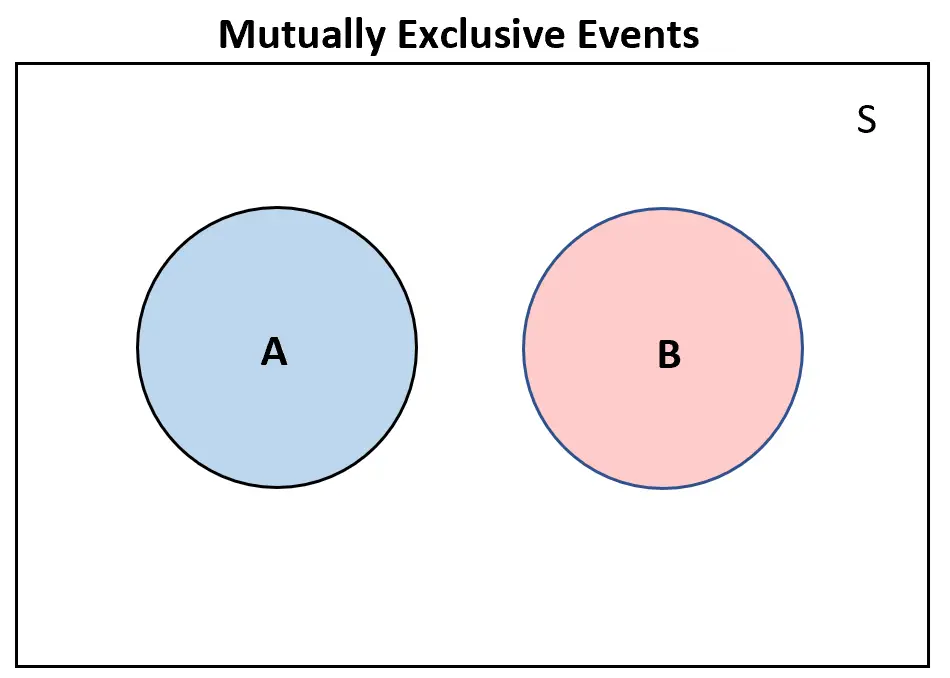
على العكس من ذلك، إذا كان هناك حدثان شاملان لبعضهما البعض ، فسيكون هناك على الأقل بعض التداخل في مخطط فين:

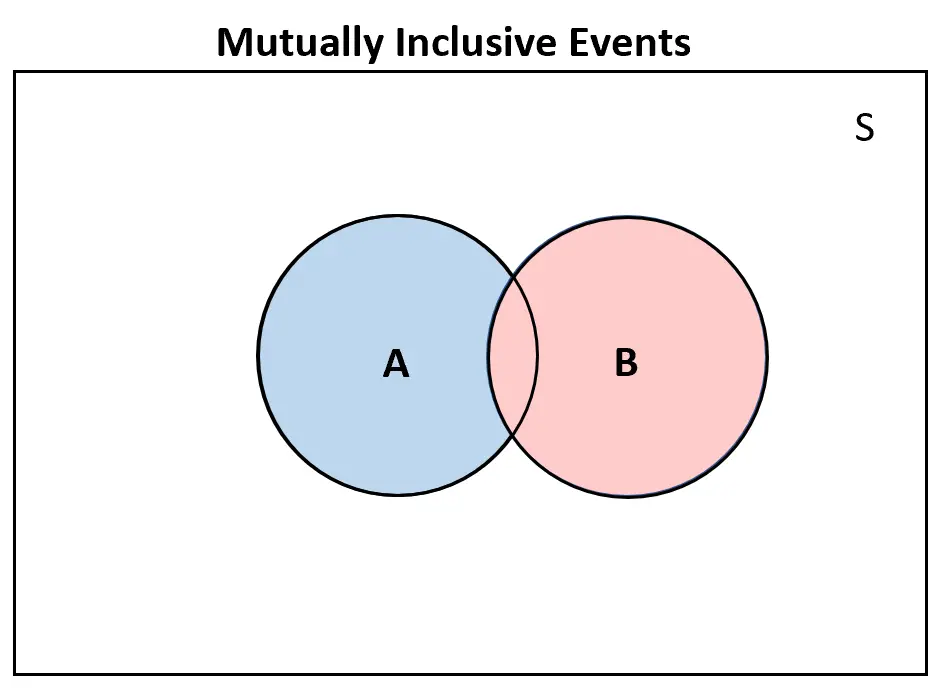
مصادر إضافية

مقدمة في الاحتمال النظري
القاعدة العامة للضرب
ما هي الأحداث المنفصلة؟