كيفية إنشاء منحنى roc في sas

الانحدار اللوجستي هو طريقة يمكننا استخدامها لتناسب نموذج الانحدار عندما يكون متغير الاستجابة ثنائيًا.

لتقييم مدى ملاءمة نموذج الانحدار اللوجستي لمجموعة البيانات، يمكننا النظر إلى المقياسين التاليين:

• الحساسية: احتمال أن يتنبأ النموذج بنتيجة إيجابية لملاحظة ما عندما تكون النتيجة إيجابية بالفعل. ويسمى هذا أيضًا “المعدل الإيجابي الحقيقي”.
• الخصوصية: احتمال أن يتنبأ النموذج بنتيجة سلبية لملاحظة ما عندما تكون النتيجة سلبية بالفعل. ويسمى هذا أيضًا “المعدل السلبي الحقيقي”.

إحدى الطرق لتصور هذين القياسين هي إنشاء منحنى ROC ، والذي يرمز إلى منحنى “خاصية تشغيل جهاز الاستقبال”. هذا رسم بياني يعرض حساسية وخصوصية نموذج الانحدار اللوجستي.

يوضح المثال التالي خطوة بخطوة كيفية إنشاء وتفسير منحنى ROC في SAS.

الخطوة 1: إنشاء مجموعة البيانات

أولاً، سنقوم بإنشاء مجموعة بيانات تحتوي على معلومات حول المتغيرات التالية لـ 18 طالبًا:

• القبول في كلية معينة (1 = نعم، 0 = لا)
• المعدل التراكمي (مقياس من 1 إلى 4)
• درجة ACT (مقياس من 1 إلى 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

الخطوة 2: ملائمة نموذج الانحدار اللوجستي وإنشاء منحنى ROC

بعد ذلك، سوف نستخدم لوجستيات proc لتناسب نموذج الانحدار اللوجستي، باستخدام “القبول” كمتغير الاستجابة و”gpa” و”act” كمتغيرات متوقعة.

سنحدد التناقص حتى تعرف SAS كيفية التنبؤ باحتمال أن يأخذ متغير الاستجابة القيمة 1.

سنستخدم أيضًا plots(only)=roc لإنشاء منحنى ROC للنموذج:

 /*fit logistic regression model & create ROC curve*/
proc logistic data =my_data descending plots ( only )=roc;
  model acceptance = gpa act;
run ;

الخطوة 3: تفسير منحنى ROC

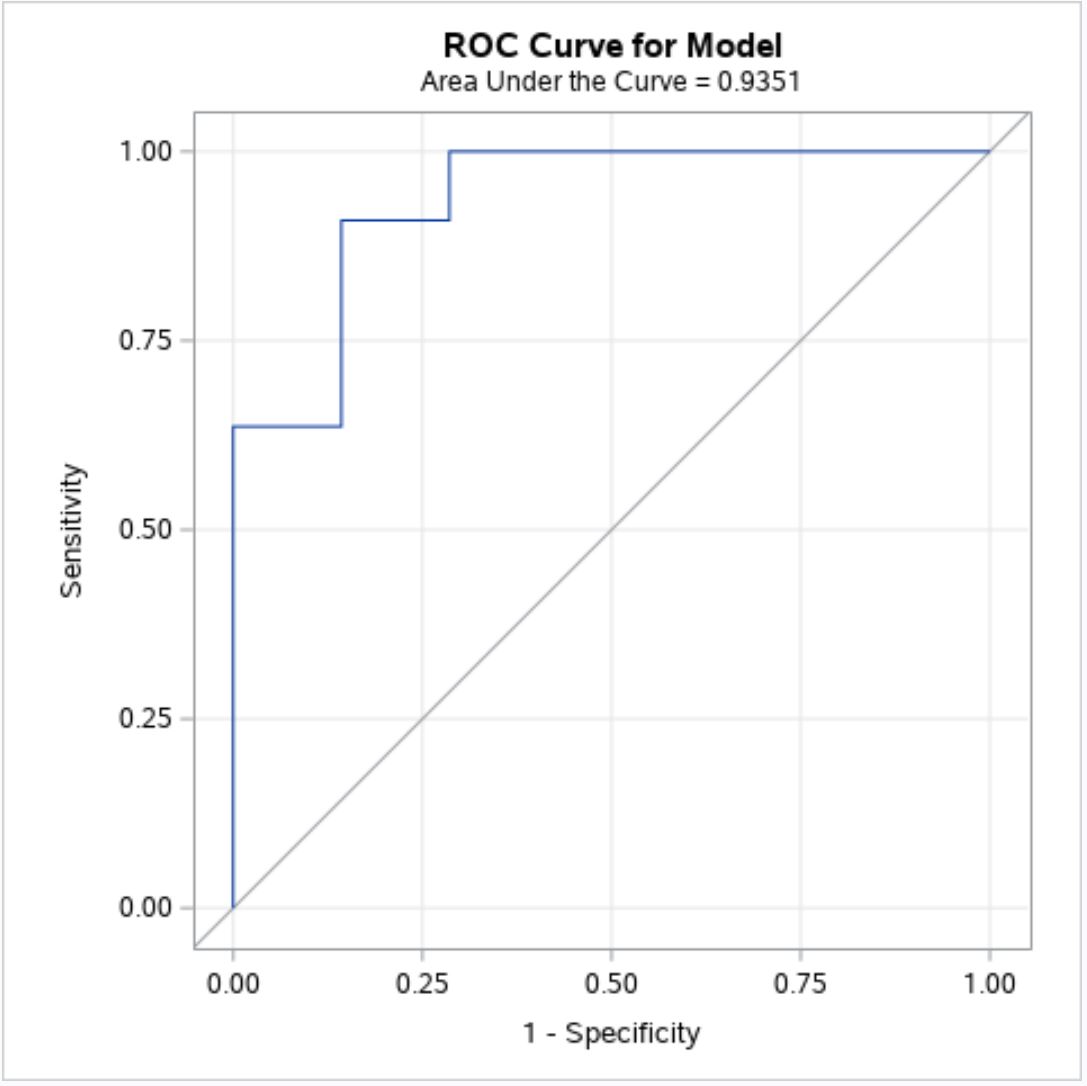
كلما اقترب منحنى ROC من الزاوية اليسرى العليا من المخطط، كلما كان النموذج يتنبأ بقيمة قيم الاستجابة في مجموعة البيانات بشكل أفضل.

من الرسم البياني أعلاه، يمكننا أن نرى أن منحنى ROC الأزرق يميل إلى احتضان الزاوية اليسرى العليا، مما يشير إلى أن نموذج الانحدار اللوجستي يقوم بعمل جيد في التنبؤ بقيمة قيم الاستجابة.

لتحديد مدى ملاءمة نموذج الانحدار اللوجستي للبيانات، يمكننا حساب AUC – المنطقة الواقعة أسفل المنحنى – والتي تخبرنا بمقدار قطعة الأرض الموجودة تحت المنحنى.

كلما اقتربت AUC من 1، كان النموذج أفضل. النموذج الذي تبلغ فيه المساحة تحت المنحنى 0.5 ليس أفضل من النموذج الذي يقوم بتصنيفات عشوائية.

تحت عنوان الرسم البياني أعلاه، يمكننا أن نرى أن AUC لهذا النموذج هو 0.9351 .

وبما أن هذه القيمة قريبة من الواحد فهذا يؤكد أن النموذج يتنبأ بقيمة قيم الاستجابة بشكل جيد.

يمكننا أيضًا استخدام قيمة AUC لمقارنة مدى ملاءمة نماذج الانحدار اللوجستي المختلفة.

على سبيل المثال، لنفترض أننا قمنا بتركيب نموذجين مختلفين للانحدار اللوجستي وحساب قيم AUC لكل منهما:

• الجامعة الأمريكية للنموذج 1: 0.9351
• الجامعة الأمريكية للنموذج 2: 0.8140

نظرًا لأن المساحة تحت المنحنى (AUC) للنموذج 1 أكبر، فإن هذا يخبرنا أن النموذج 1 يقوم بعمل أفضل في ملاءمة البيانات من النموذج 2.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ العمليات الشائعة الأخرى في SAS:

كيفية إجراء الانحدار الخطي البسيط في SAS
كيفية إجراء الانحدار الخطي المتعدد في SAS
كيفية إجراء الانحدار اللوجستي في SAS