مقدمة إلى تحليل التباين (ancova)
ANCOVA تعني “تحليل التباين”. لفهم كيفية عمل تحليل التباين (ANCOVA)، من المفيد أن نفهم تحليل التباين (ANCOVA) أولاً.
أنوفا _ يستخدم (تحليل التباين) لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر.
على سبيل المثال، لنفترض أننا نريد معرفة ما إذا كانت تقنية الدراسة تؤثر على درجات امتحان فئة من الطلاب أم لا. قمنا بتقسيم الفصل إلى ثلاث مجموعات بشكل عشوائي. تستخدم كل مجموعة أسلوب دراسة مختلفًا لمدة شهر للتحضير للامتحان. وفي نهاية الشهر، يؤدي جميع الطلاب نفس الاختبار.
لمعرفة ما إذا كان أسلوب الدراسة له تأثير على درجات الامتحانات، يمكننا إجراء تحليل التباين (ANOVA) أحادي الاتجاه، والذي سيخبرنا ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسط درجات المجموعات الثلاث.
تحليل التباين (ANCOVA) هو امتداد لتحليل التباين (ANOVA) الذي نريد من خلاله تحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين ثلاث مجموعات مستقلة أو أكثر بعد حساب متغير واحد أو أكثر.
المتغير المشترك هو متغير مستمر يختلف مع متغير الاستجابة.
على سبيل المثال، لنفترض أننا نريد معرفة ما إذا كان أسلوب الدراسة له تأثير على درجات الامتحان أم لا، لكننا نريد أن نأخذ في الاعتبار الدرجة التي حصل عليها الطالب بالفعل في الفصل . يمكننا استخدام درجتهم الحالية كمتغير مشترك وإجراء تحليل التباين المشترك (ANCOVA) لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسط درجات الاختبار للمجموعات الثلاث.
يتيح لنا ذلك اختبار ما إذا كان أسلوب الدراسة له تأثير على درجات الامتحانات أم لا بمجرد إزالة تأثير المتغير المشترك.
لذلك، إذا وجدنا أن هناك فرقًا ذا دلالة إحصائية في درجات الامتحانات بين تقنيات الدراسة الثلاثة، فيمكننا التأكد من أن هذا الاختلاف موجود حتى بعد الأخذ في الاعتبار الدرجة الحالية للطلاب في الفصل (ج’ أي إذا كانوا يقومون بعمل جيد بالفعل أو إذا كانوا في حالة جيدة بالفعل). ليس في الصف) .
افتراضات تحليل التباين (ANCOVA).
قبل إجراء تحليل التباين المشترك (ANCOVA)، من المهم التأكد من استيفاء الافتراضات التالية:
- المتغير (المتغيرات) والمتغير (المتغيرات) العامل مستقلان – يجب أن يكون المتغير المشترك ومتغير العامل مستقلين عن بعضهما البعض، لأن إضافة مصطلح متغير في النموذج يكون منطقيًا فقط إذا كان المتغير المشترك ومتغير العامل يعملان بشكل مستقل على متغير الاستجابة .
- المتغير (المتغيرات) المشتركة عبارة عن بيانات مستمرة. يجب أن تكون المتغيرات المشتركة مستمرة (أي بيانات الفاصل الزمني أو النسبة).
- تجانس التباينات – يجب أن تكون التباينات بين المجموعات متساوية تقريبًا.
- الاستقلال – يجب أن تكون الملاحظات في كل مجموعة مستقلة.
- الحالة الطبيعية – يجب أن يتم توزيع البيانات بشكل طبيعي تقريبًا في كل مجموعة.
- لا توجد قيم متطرفة – يجب ألا تكون هناك قيم متطرفة في أي من المجموعات التي يمكن أن تؤثر بشكل كبير على نتائج تحليل التباين (ANCOVA).
أنكوفا: مثال
تريد إحدى المعلمات معرفة ما إذا كانت هناك ثلاث تقنيات دراسة مختلفة تؤثر على درجات الامتحان، ولكنها تريد أن تأخذ في الاعتبار الدرجة الحالية التي حصل عليها الطالب بالفعل في الفصل.
سيتم إجراء تحليل التباين (ANCOVA) باستخدام المتغيرات التالية:
- متغير العامل: الدراسة الفنية
- المتغير: النتيجة الحالية
- متغير الاستجابة: درجة الامتحان
يعرض الجدول التالي مجموعة بيانات الطلاب الخمسة عشر الذين تم تعيينهم للمشاركة في الدراسة:
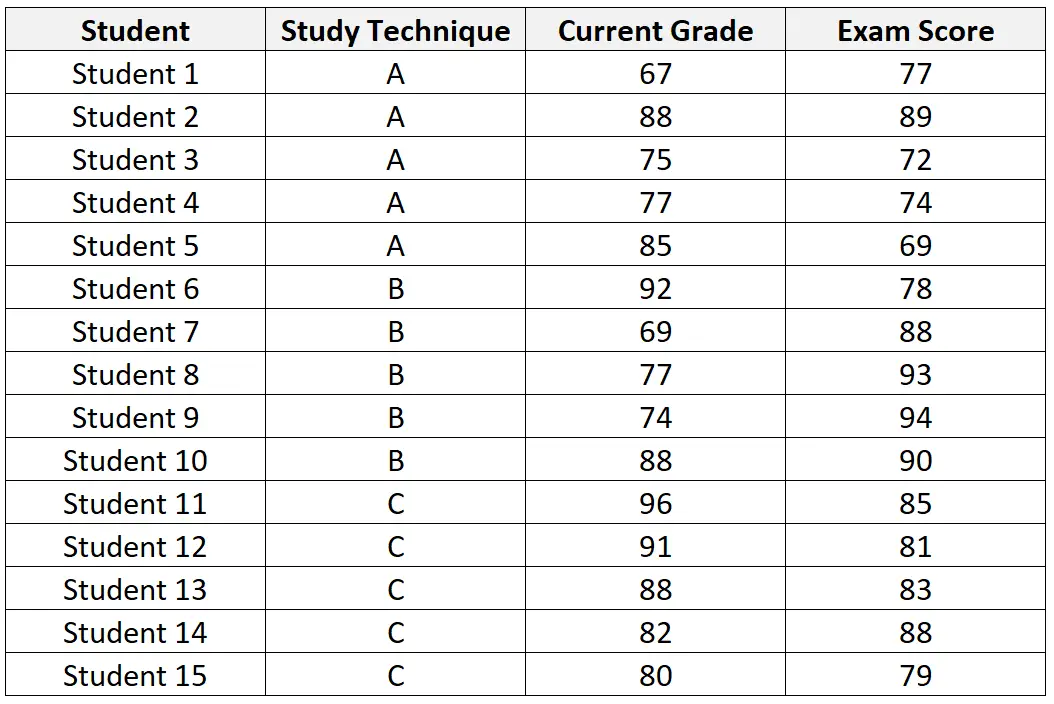
بعد إجراء تحليل التباين (ANCOVA) على مجموعة البيانات، يحصل المعلم على النتائج التالية:

القيمة p لتقنية الدراسة هي 0.03155 . وبما أن هذه القيمة أقل من 0.05، فيمكننا رفض الفرضية الصفرية القائلة بأن كل أسلوب من أساليب الدراسة يؤدي إلى نفس متوسط درجات الامتحان، حتى بعد احتساب الدرجة الحالية للطالب في الفصل .
لتحديد تقنيات الدراسة التي تنتج متوسطات مختلفة لدرجات الامتحانات، سيحتاج المعلم إلى إجراء اختبار ما بعد الاختبار .
مصادر إضافية
كيفية إجراء تحليل التباين (ANCOVA) في Excel
كيفية إجراء تحليل التباين (ANCOVA) في R
كيفية إجراء تحليل التباين (ANCOVA) في بايثون
الاختلافات بين أنوفا، أنكوفا، مانوفا ومانكوفا