الفرضيات الخمس لارتباط بيرسون

يقيس معامل ارتباط بيرسون (المعروف أيضًا باسم “معامل الارتباط بين المنتج واللحظة”) الارتباط الخطي بين متغيرين.

يأخذ دائمًا قيمة بين -1 و1 حيث:

• يشير -1 إلى وجود علاقة خطية سلبية تمامًا بين متغيرين
• يشير 0 إلى عدم وجود علاقة خطية بين متغيرين
• يشير الشكل 1 إلى وجود علاقة خطية إيجابية تمامًا بين متغيرين

ومع ذلك، قبل حساب معامل ارتباط بيرسون بين متغيرين، يجب التأكد من استيفاء خمسة افتراضات:

1. مستوى القياس: يجب قياس كلا المتغيرين على مستوى الفترة أو النسبة .

2. العلاقة الخطية: يجب أن تكون هناك علاقة خطية بين المتغيرين.

3. الحالة الطبيعية: يجب أن يكون لكلا المتغيرين توزيع طبيعي تقريبًا.

4. الأزواج المرتبطة: يجب أن تحتوي كل ملاحظة في مجموعة البيانات على زوج من القيم.

5. لا توجد قيم متطرفة: يجب ألا تكون هناك قيم متطرفة في مجموعة البيانات.

وفي هذه المقالة نقدم شرحًا لكل افتراض بالإضافة إلى كيفية تحديد ما إذا كان الافتراض قد تحقق أم لا.

الفرضية 1: مستوى القياس

لحساب معامل ارتباط بيرسون بين متغيرين، يجب قياس كلا المتغيرين على مستوى الفاصل أو النسبة .

ويقدم الرسم التالي شرحاً سريعاً للمستويات الأربعة التي يمكن قياس المتغيرات فيها:

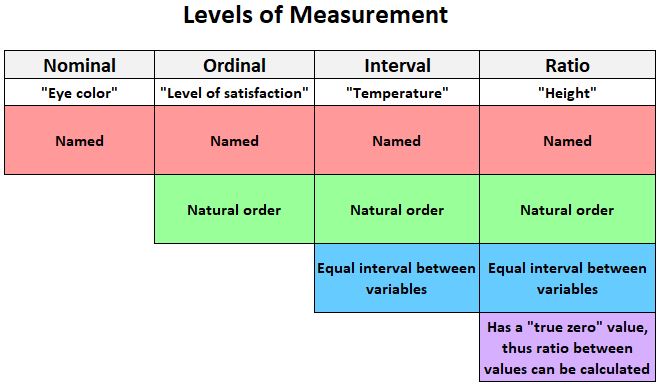
فيما يلي بعض الأمثلة على المتغيرات التي يمكن قياسها على مقياس فاصل :

• درجة الحرارة: تقاس بالفهرنهايت أو مئوية
• درجات الائتمان: تقاس من 300 إلى 850
• درجات اختبار SAT: تقاس من 400 إلى 1600

فيما يلي بعض الأمثلة على المتغيرات التي يمكن قياسها على مقياس النسبة :

• الارتفاع: يُقاس بالسنتيمتر، البوصة، القدم، إلخ.
• الوزن: يقاس بالكيلوجرام والجنيه وما إلى ذلك.
• الطول: يُقاس بالسنتيمتر، البوصة، القدم، إلخ.

إذا تم قياس المتغيرات على المستوى الترتيبي ، فأنت بحاجة إلى حساب معامل ارتباط سبيرمان بينهما.

ذات صلة: مستويات القياس: الاسمية والترتيبية والفاصلة والنسبة

الفرضية 2: العلاقة الخطية

لحساب معامل ارتباط بيرسون بين متغيرين، يجب أن تكون هناك علاقة خطية بين المتغيرين.

أسهل طريقة لاختبار هذه الفرضية هي ببساطة إنشاء مخطط مبعثر للمتغيرين. إذا كانت النقاط على المخطط تتبع خطًا مستقيمًا تقريبًا، فتوجد علاقة خطية:

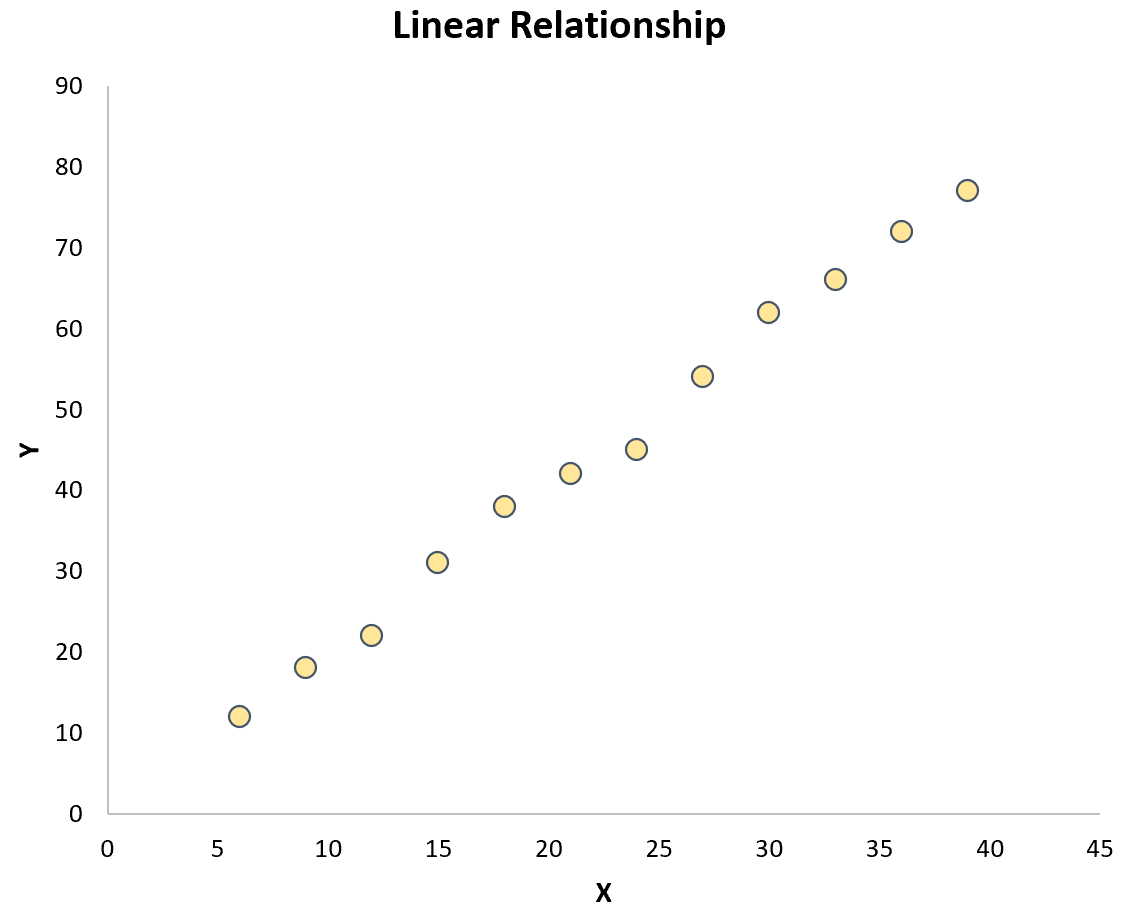
ومع ذلك، إذا كانت النقاط منتشرة عشوائيًا عبر المخطط أو كان لها نوع آخر من العلاقات (مثل العلاقات التربيعية)، فلن توجد علاقة خطية بين المتغيرات:

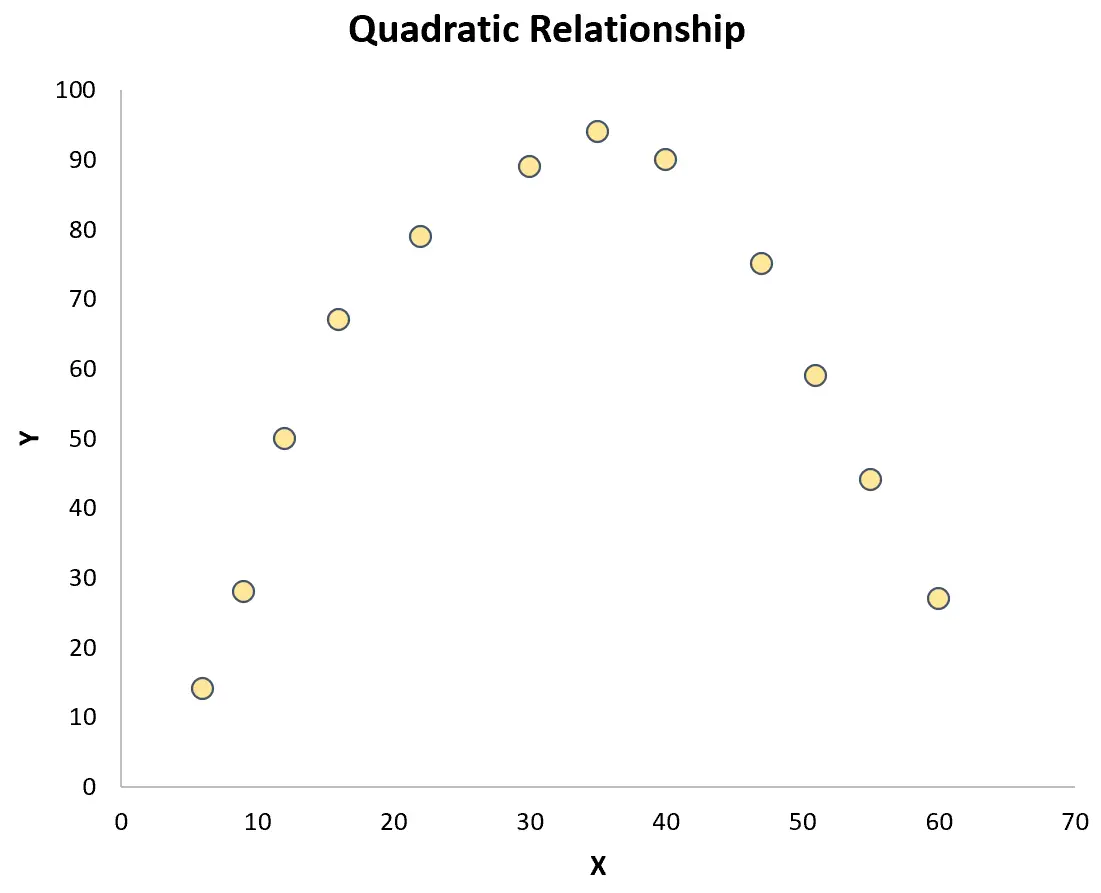
في هذه الحالة، لن يتمكن معامل ارتباط بيرسون من التقاط العلاقة بين المتغيرات بشكل كافٍ.

الفرضية 3: الحياة الطبيعية

ويفترض معامل ارتباط بيرسون أيضًا أن المتغيرين موزعان بشكل طبيعي تقريبًا .

يمكنك التحقق من هذا الافتراض بشكل مرئي عن طريق إنشاء رسم بياني أو مخطط QQ لكل متغير.

1. الرسم البياني

إذا كان الرسم البياني لمجموعة البيانات على شكل جرس تقريبًا، فمن المحتمل أن يتم توزيع البيانات بشكل طبيعي.

2. كيو كيو لاند

مخطط QQ، وهو اختصار لعبارة “Quantile-Quantile”، هو نوع من المخططات التي تعرض الكميات النظرية على طول المحور السيني (أي المكان الذي ستكون فيه بياناتك إذا اتبعت التوزيع الطبيعي) وكميات العينات على طول المحور الصادي. (أي المكان الذي توجد فيه بياناتك فعليًا).

إذا كانت قيم البيانات تتبع خطًا مستقيمًا تقريبًا يشكل زاوية قدرها 45 درجة، فمن المفترض أن يتم توزيع البيانات بشكل طبيعي.

يمكنك أيضًا إجراء اختبار إحصائي رسمي لتحديد ما إذا كان المتغير موزعًا بشكل طبيعي.

إذا كانت القيمة p للاختبار أقل من مستوى معين من الأهمية (مثل α = 0.05)، فهذا يعني أن لديك أدلة كافية للقول بأن البيانات لا يتم توزيعها بشكل طبيعي.

هناك ثلاثة اختبارات إحصائية تستخدم عادة لاختبار الحالة الطبيعية:

1. اختبار جارك بيرا

• كيفية إجراء اختبار جارك بيرا في إكسيل
• كيفية إجراء اختبار Jarque-Bera في R
• كيفية إجراء اختبار Jarque-Bera في بايثون

2. اختبار شابيرو ويلك

• كيفية إجراء اختبار شابيرو ويلك في R
• كيفية إجراء اختبار شابيرو ويلك في بايثون

3. اختبار كولموجوروف-سميرنوف

• كيفية إجراء اختبار Kolmogorov-Smirnov في R
• كيفية إجراء اختبار Kolmogorov-Smirnov في بايثون

الفرضية 4: أزواج ذات صلة

يفترض معامل ارتباط بيرسون أيضًا أن كل ملاحظة في مجموعة البيانات يجب أن تحتوي على زوج من القيم.

من السهل التحقق من هذه الفرضية. على سبيل المثال، إذا كنت تحسب الارتباط بين الوزن والطول، فما عليك سوى التحقق من أن كل ملاحظة في مجموعة البيانات تحتوي على مقياس للوزن ومقياس للطول.

الفرضية 5: لا القيم المتطرفة

ويفترض معامل ارتباط بيرسون أيضًا عدم وجود قيم متطرفة في مجموعة البيانات، لأن القيم المتطرفة تؤثر بشدة على حساب معامل الارتباط.

لتوضيح ذلك، خذ بعين الاعتبار مجموعة البيانات التالية:

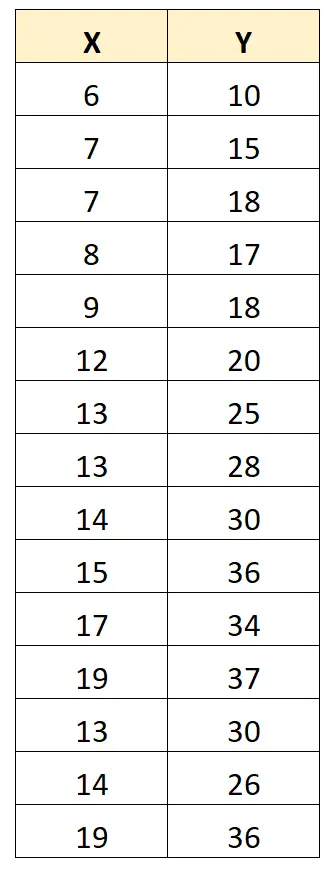
معامل ارتباط بيرسون بين X و Y هو 0.949 .

ومع ذلك، لنفترض أن لدينا قيمة متطرفة في مجموعة البيانات:

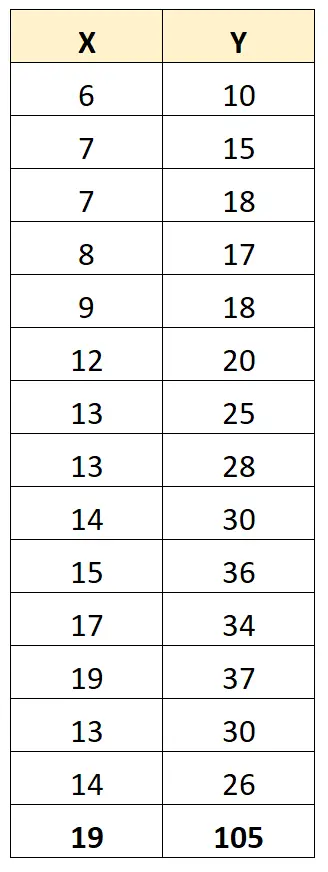
أصبح معامل ارتباط بيرسون بين X و Y الآن 0.711 .

تغير القيم المتطرفة بشكل كبير معامل ارتباط بيرسون بين المتغيرين. في هذه الحالة، قد يكون من المنطقي إزالة القيمة المتطرفة من مجموعة البيانات.

ذات صلة: الدليل الكامل: متى يجب إزالة القيم المتطرفة في البيانات

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول ارتباط بيرسون:

مقدمة لمعامل ارتباط بيرسون
كيفية الإبلاغ عن ارتباط بيرسون بتنسيق APA
كيفية حساب معامل ارتباط بيرسون يدويًا