كيفية حساب قيمة p يدويًا من اختبار t
أحد الاختبارات الأكثر استخدامًا في الإحصاء هو اختبار t ، والذي يُستخدم غالبًا لتحديد ما إذا كان متوسط عدد السكان يساوي قيمة معينة.
على سبيل المثال، لنفترض أننا نريد معرفة ما إذا كان متوسط ارتفاع نوع معين من النباتات يساوي 15 بوصة. لاختبار ذلك، يمكننا جمع عينة عشوائية من 20 نباتًا، وإيجاد متوسط العينة والانحراف المعياري للعينة، وإجراء اختبار t لتحديد ما إذا كان متوسط الارتفاع هو 15 بوصة بالفعل.
الفرضيات الصفرية والبديلة للاختبار هي كما يلي:
ح 0 : μ = 15
ح أ : μ ≠ 15
صيغة إحصائية الاختبار هي:
ر = ( X -μ) / (ق/ √n )
حيث x هو متوسط العينة، μ هو المتوسط الافتراضي (في مثالنا سيكون 15)، s هو الانحراف المعياري للعينة، و n هو حجم العينة.
بمجرد أن نعرف قيمة t ، يمكننا استخدام برنامج إحصائي أو آلة حاسبة عبر الإنترنت للعثور على القيمة p المقابلة. إذا كانت القيمة p أقل من مستوى ألفا معين (الاختيارات الشائعة هي 0.01 و0.05 و0.10)، فيمكننا رفض فرضية العدم ونستنتج أن متوسط ارتفاع النبات لا يساوي 15 بوصة.
ومع ذلك، من الممكن أيضًا تقدير قيمة الاختبار يدويًا باستخدام جدول توزيع t . وفي هذه المقالة سنشرح كيفية القيام بذلك.
مثال: الحساب اليدوي للقيمة p من اختبار t
المشكلة : يريد بوب معرفة ما إذا كان متوسط ارتفاع نوع معين من النباتات يساوي 15 بوصة. ولاختبار ذلك، قام بجمع عينة عشوائية من 20 نباتًا ووجد أن متوسط العينة هو 14 بوصة والانحراف المعياري للعينة هو 3 بوصات. قم بإجراء اختبار t باستخدام مستوى ألفا قدره 0.05 لتحديد ما إذا كان متوسط ارتفاع السكان الحقيقي هو 15 بوصة بالفعل.
حل:
الخطوة الأولى: تحديد الفرضيات الصفرية والبديلة.
ح 0 : μ = 15
ح أ : μ ≠ 15
الخطوة 2: ابحث عن إحصائية الاختبار.
t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1.49
الخطوة 3: ابحث عن القيمة الاحتمالية لإحصائيات الاختبار.
للعثور على القيمة p يدويًا، نحتاج إلى استخدام جدول توزيع t مع درجات حرية n-1. في مثالنا، حجم العينة هو n = 20، لذا n-1 = 19.
في جدول توزيع t أدناه، نحتاج إلى إلقاء نظرة على الصف الذي يتوافق مع “19” على الجانب الأيسر ومحاولة العثور على القيمة المطلقة لإحصاء الاختبار لدينا 1.49 .
لاحظ أن 1.49 لا يظهر في الجدول ولكنه يقع بين القيمتين 1.328 و 1.729 .
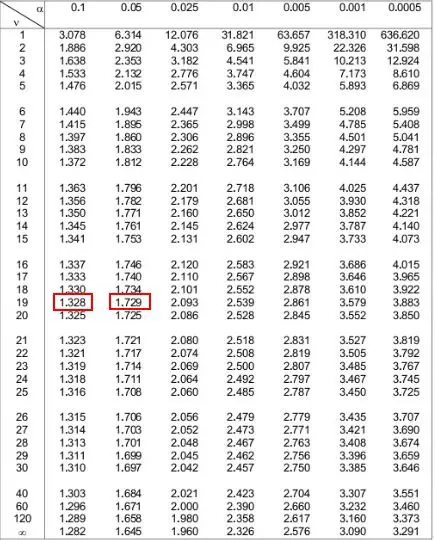
ثم يمكننا أن ننظر إلى مستويي ألفا الموجودين في أعلى الجدول اللذين يتوافقان مع هذين الرقمين. نرى أنهم 0.1 و 0.05 .
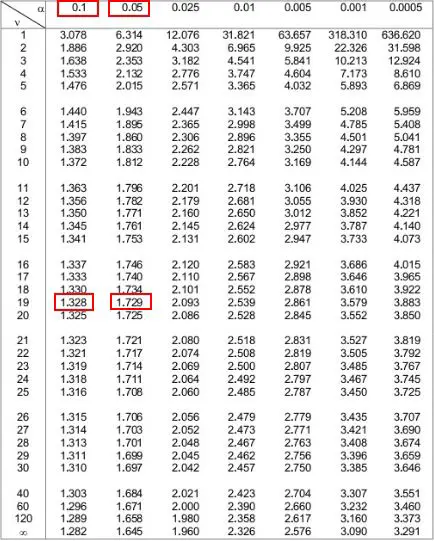
وهذا يعني أن القيمة p للاختبار أحادي الطرف تتراوح بين 0.1 و0.05. دعنا نسميها .075. نظرًا لأن اختبار t الخاص بنا ذو طرفين، فنحن بحاجة إلى ضرب هذه القيمة بـ 2. لذا، فإن القيمة p المقدرة لدينا هي 0.075 * 2 = 0.15 .
الخطوة 4: استخلاص النتيجة.
وبما أن هذه القيمة p ليست أقل من مستوى ألفا المختار وهو 0.05، فلا يمكننا رفض فرضية العدم. وبالتالي، ليس لدينا ما يكفي من الأدلة لنقول أن متوسط الارتفاع الحقيقي لهذا النوع من النباتات هو أي شيء آخر غير 15 بوصة.
التحقق من النتائج باستخدام الآلة الحاسبة
يمكننا توصيل إحصائية اختبار t ودرجات الحرية الخاصة بنا إلى حاسبة القيمة الاحتمالية عبر الإنترنت لمعرفة مدى قرب القيمة الاحتمالية المقدرة لدينا من القيمة الاحتمالية الحقيقية:

القيمة p الحقيقية هي 0.15264 ، وهي قريبة جدًا من القيمة p المقدرة لدينا والتي تبلغ 0.15 .
خاتمة
لقد رأينا في هذه المقالة أنه من الممكن تقدير القيمة الاحتمالية لاختبار t يدويًا باستخدام جدول توزيع t. ومع ذلك، في معظم السيناريوهات، لن تضطر أبدًا إلى حساب القيمة الاحتمالية يدويًا، ويمكنك استخدام إما برامج إحصائية مثل R وExcel أو آلة حاسبة عبر الإنترنت للعثور على القيمة الاحتمالية الدقيقة للاختبار.
في معظم الحالات، خاصة في الدراسات والتجارب الإحصائية الصارمة، ستحتاج إلى استخدام الآلة الحاسبة للعثور على القيمة الاحتمالية الدقيقة من اختبار t لتكون دقيقة قدر الإمكان، ولكن من الجيد أن تعرف أنه يمكنك دائمًا تقدير القيمة الاحتمالية يدويًا القيمة p من اختبار t إذا كنت في حاجة ماسة لذلك.