ما أهمية الانحراف المعياري؟ (شرح + أمثلة)

يستخدم الانحراف المعياري لقياس توزيع القيم في العينة.

يمكننا استخدام الصيغة التالية لحساب الانحراف المعياري لعينة معينة:

√ Σ(س _ط – س _بار ) ² / (ن-1)

ذهب:

• Σ: رمز يعني “المجموع”
• _xi : القيمة ⁱ للعينة
• _شريط x: يعني العينة
• ن: حجم العينة

كلما زادت قيمة الانحراف المعياري، زادت تشتت القيم في العينة. وعلى العكس من ذلك، كلما انخفضت قيمة الانحراف المعياري، كلما تم تجميع القيم بشكل أوثق.

السؤال الذي يطرحه الطلاب غالبًا هو: ما أهمية الانحراف المعياري؟

الجواب: الانحراف المعياري مهم لأنه يخبرنا بتوزيع القيم في مجموعة بيانات معينة.

نقوم بتحليل مجموعة بيانات كلما أردنا العثور على المقاييس التالية:

• مركز مجموعة البيانات . الطريقة الأكثر شيوعًا لقياس “المركز” هي استخدام المتوسط والوسيط.
• توزيع القيم في مجموعة البيانات . الطريقة الأكثر شيوعًا لقياس الانتشار هي استخدام الانحراف المعياري.

ومن خلال معرفة مكان المركز وما هو توزيع القيم، يمكننا أن نفهم جيدًا توزيع القيم في أي مجموعة بيانات.

توضح الأمثلة التالية أهمية الانحراف المعياري في الممارسة العملية.

مثال 1: توزيع الرواتب

لنفترض أن متوسط الراتب في الشركة (أ) هو 80 ألف دولار والانحراف المعياري هو 20 ألف دولار. نظرًا لأن الانحراف المعياري كبير جدًا، فليس هناك ما يضمن أنك ستحصل على ما يقرب من 80 ألف دولار سنويًا إذا كنت تعمل في هذه الشركة نظرًا لوجود مثل هذا الاختلاف في الرواتب.

على العكس من ذلك، لنفترض أن متوسط الراتب في الشركة (ب) هو أيضًا 80 ألف دولار، ولكن الانحراف المعياري هو 4000 دولار فقط. نظرًا لأن هذا الانحراف المعياري صغير جدًا، يمكنك التأكد من أنه سيتم الدفع لك بما يقرب من 80 ألف دولار نظرًا لوجود تباين بسيط جدًا في الرواتب.

إذا أنشأنا مخططًا مربعًا لتصور توزيع الرواتب في هاتين الشركتين، فقد يبدو كما يلي:

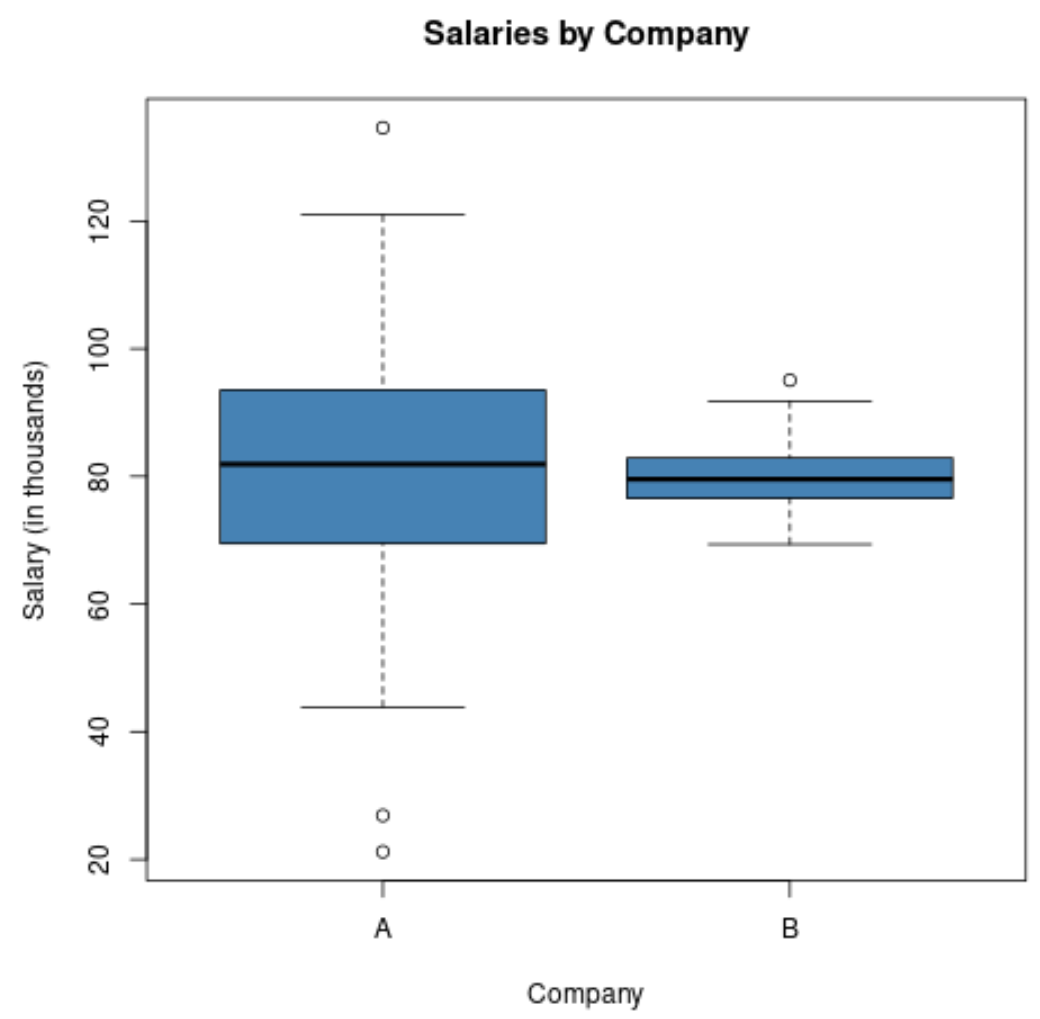
لاحظ أن طول مخطط الصندوق للشركة (أ) أكبر لأن الانحراف المعياري للأجور أعلى بكثير.

كلا الشركتين لديهما نفس متوسط الراتب، لكن فجوة الرواتب أعلى بكثير في الشركة أ.

مثال 2: توزيع أسعار المساكن

افترض أن متوسط سعر السكن في الحي أ هو 250 ألف دولار والانحراف المعياري هو 50 ألف دولار. وبما أن الانحراف المعياري كبير جدًا، فهذا يعني أن بعض أسعار المنازل ستكون أعلى بكثير من 250 ألف دولار والبعض الآخر ستكون أقل بكثير. إذا نظرت إلى أي منزل في هذا الحي، فليس هناك ما يضمن أن السعر سيكون قريبًا من المتوسط.

وعلى العكس من ذلك، لنفترض أن متوسط سعر المنزل في الحي “ب” هو أيضًا 250 ألف دولار، ولكن الانحراف المعياري يبلغ 10 آلاف دولار فقط. نظرًا لأن هذا الانحراف المعياري صغير جدًا، يمكنك التأكد من أن أي منزل تنظر إليه في الحي من المحتمل أن يكون مغلقًا بهذا السعر.

إذا قمنا بإنشاء مخطط مربع لتصور توزيع أسعار المنازل في هذين الحيين، فقد يبدو كما يلي:

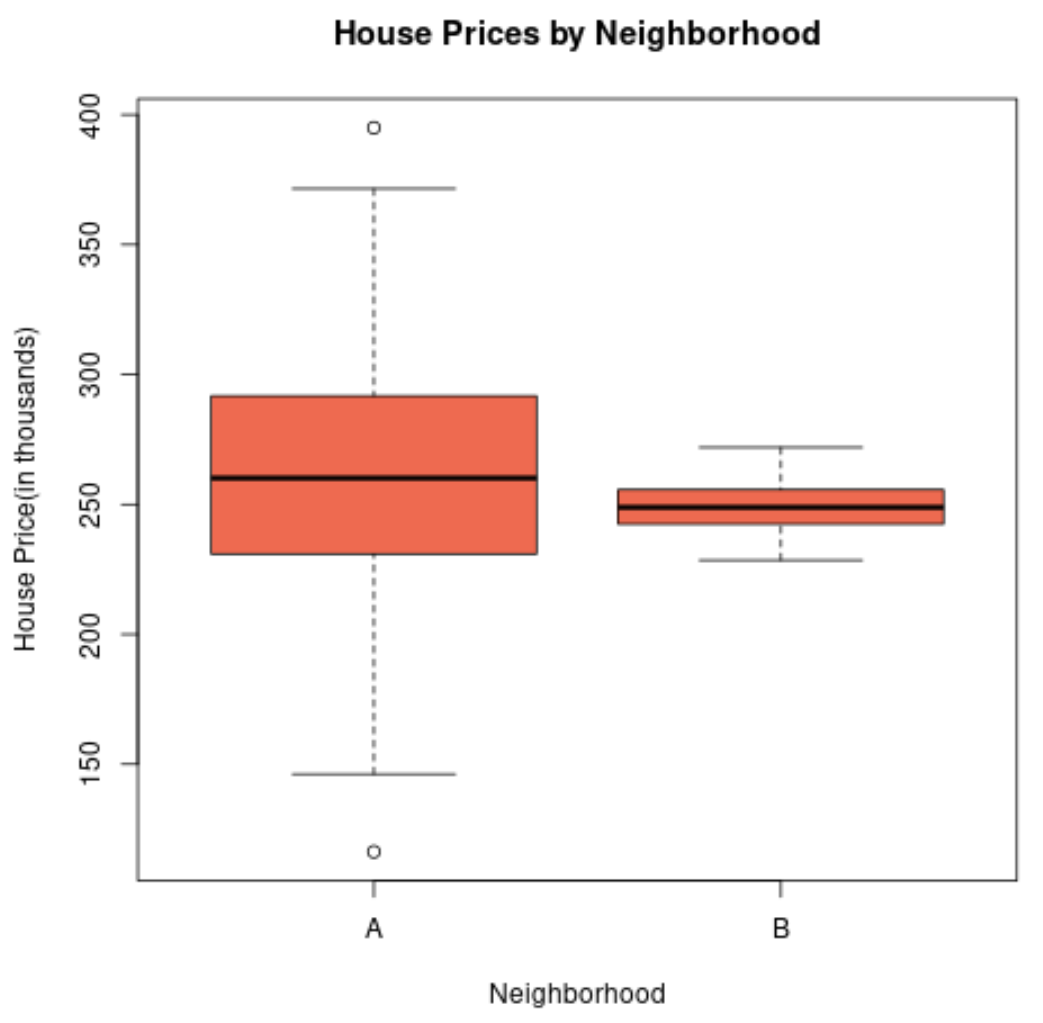
يكون طول قطعة الأرض المربعة للحي A أكبر نظرًا لأن الانحراف المعياري لأسعار العقارات أعلى بكثير.

في الواقع، تتراوح أسعار المساكن من أقل من 150 ألف دولار إلى أكثر من 400 ألف دولار للحي أ، في حين تتراوح الأسعار فقط من حوالي 230 ألف دولار إلى 270 ألف دولار للحي ب.

وببساطة من خلال معرفة الانحراف المعياري لأسعار المنازل في كل حي، يمكننا معرفة مقدار التباين المتوقع في الأسعار في كل حي.

مصادر إضافية

ما الذي يعتبر انحرافا معياريا جيدا؟
النطاق مقابل. الانحراف المعياري: متى يتم استخدام كل منهما
معامل الاختلاف مقابل الانحراف المعياري: الفرق