الانحراف المتوسط المطلق مقابل الانحراف المعياري: ما الفرق؟
يعد الانحراف المعياري أحد أكثر الطرق شيوعًا لقياس انتشار مجموعة البيانات.
يتم حسابه على النحو التالي:
الانحراف المعياري = √( Σ(x i – x ) 2 / n )
هناك طريقة أخرى لقياس توزيع الملاحظات في مجموعة بيانات وهي متوسط الانحراف المطلق .
يتم حسابه على النحو التالي:
متوسط الانحراف المطلق = Σ|x i – x | /لا
يشرح هذا البرنامج التعليمي الاختلافات بين هذين المقياسين بالإضافة إلى أمثلة حول كيفية حساب كل منهما.
أوجه التشابه والاختلاف
كما يوحي اسمها، يحاول الانحراف المعياري ومتوسط الانحراف المطلق تحديد الانحراف النموذجي للملاحظات عن المتوسط في مجموعة بيانات معينة.
ومع ذلك، تختلف الطريقة المستخدمة لكل مقياس.
الانحراف المعياري
يجد الانحراف المعياري الفرق التربيعي بين كل ملاحظة ومتوسط مجموعة البيانات. ثم يقوم بعد ذلك بحساب متوسط هذه الاختلافات التربيعية ويأخذ الجذر التربيعي.
وهذا يتركنا مع رقم يمثل الانحراف “المعياري” أو النموذجي للملاحظة عن المتوسط.
يعني الانحراف المطلق
على العكس من ذلك، يعني الانحراف المطلق العثور على الانحراف المطلق بين كل ملاحظة ومتوسط مجموعة البيانات. ثم يجد متوسط هذه الانحرافات.
وهذا يتركنا مع رقم يمثل متوسط انحراف الملاحظات عن المتوسط.
وبما أن الانحراف المعياري يجد فروقًا مربعة، فسيكون دائمًا مساويًا أو أكبر من متوسط الانحراف المطلق.
عندما تكون القيم المتطرفة موجودة، سيكون الانحراف المعياري أكبر بكثير من متوسط الانحراف المطلق. ويوضح المثال التالي هذه النقطة.
مثال: متوسط الانحراف المطلق عن الانحراف المعياري
لنفترض أن لدينا مجموعة البيانات التالية المكونة من 8 قيم:
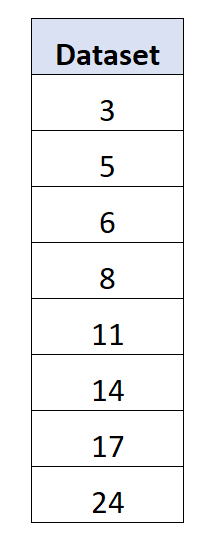
المتوسط يتحول إلى 11 .
لذلك، يمكننا حساب متوسط الانحراف المطلق على النحو التالي:
متوسط الانحراف المطلق = (|3-11| + |5-11| + |6-11| + |8-11| + |11-11| + |14-11| + |17-11| + |24- 11|) / 8 = 5.5 .
ونقوم بحساب الانحراف المعياري على النحو التالي:
الانحراف المعياري = √ ((3-11) 2 + (5-11) 2 + (6-11) 2 + (8-11) 2 + (11-11) 2 + (14-11) 2 + (17- 11) 2 + (24-11) 2 )/8) = 6.595 .
كما ذكرنا سابقًا، سيكون الانحراف المعياري دائمًا مساويًا أو أكبر من متوسط الانحراف المطلق.
ومع ذلك، فإن الفرق بين الانحراف المعياري ومتوسط الانحراف المطلق سيكون كبيرًا بشكل خاص إذا كانت هناك قيم متطرفة في مجموعة البيانات.
على سبيل المثال، ضع في اعتبارك مجموعة البيانات التالية ذات قيمة متطرفة للقيمة الأخيرة:
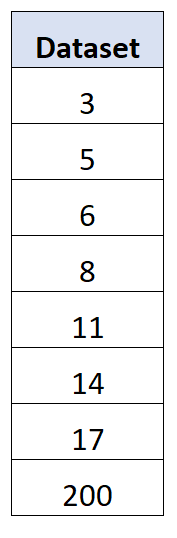
وتبين أن الانحراف المعياري لمجموعة البيانات هذه هو 63.27 في حين أن متوسط الانحراف المطلق هو 41.75 .
يؤدي الحد الأقصى إلى أن يكون الانحراف المعياري أكبر بكثير من متوسط الانحراف المطلق.
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر