مجموعة التحقق من الصحة ومجموعة الاختبار: ما الفرق؟

عندما نقوم بتكييف خوارزمية التعلم الآلي مع مجموعة بيانات، فإننا عادةً ما نقسم مجموعة البيانات إلى ثلاثة أجزاء:

1. مجموعة التدريب : تستخدم لتدريب النموذج.

2. مجموعة التحقق من الصحة : تستخدم لتحسين معلمات النموذج.

3. مجموعة الاختبار : تستخدم للحصول على تقدير غير متحيز لأداء النموذج النهائي.

يقدم الرسم البياني التالي شرحًا مرئيًا لهذه الأنواع الثلاثة المختلفة من مجموعات البيانات:

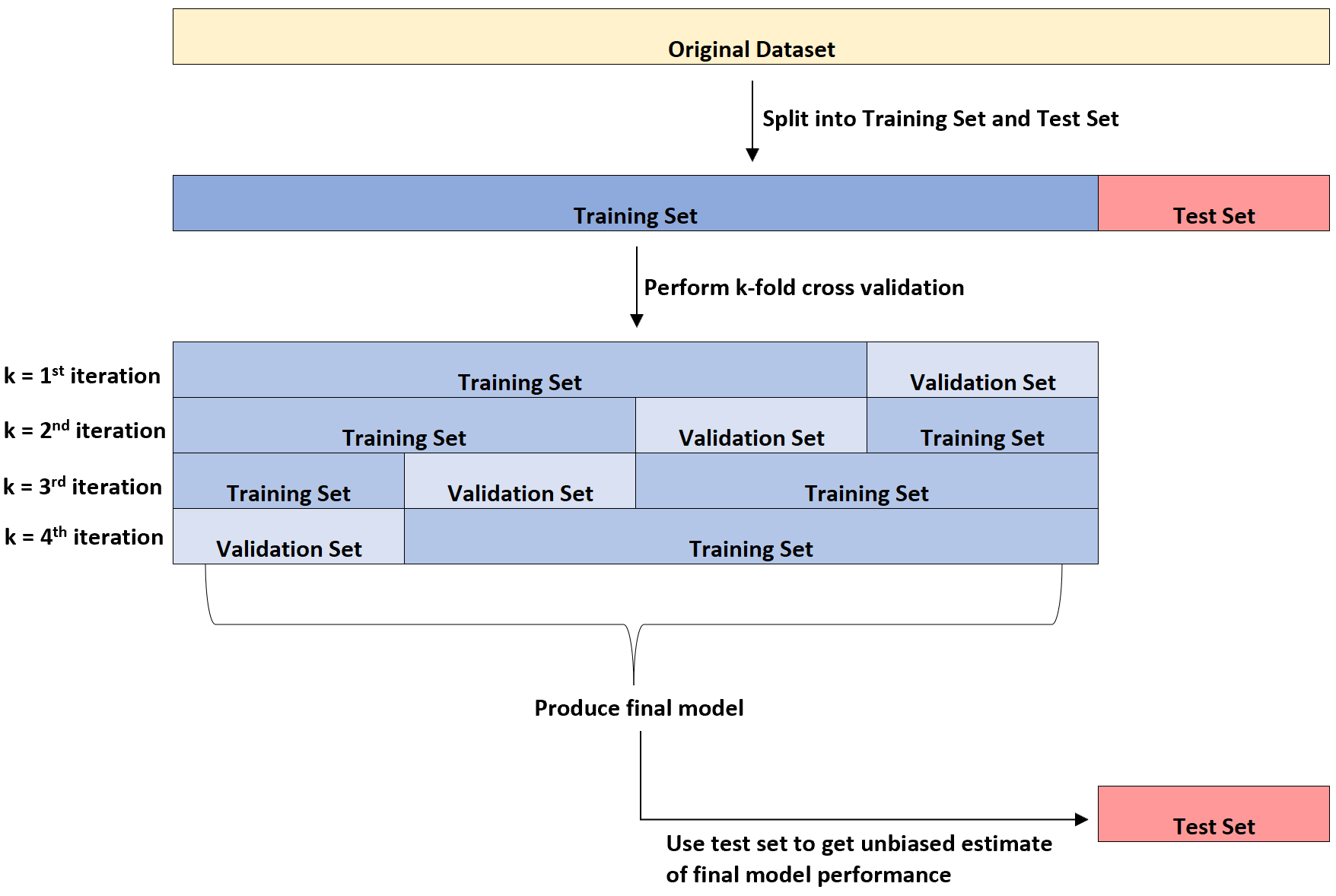
إحدى نقاط الارتباك للطلاب هي الفرق بين مجموعة التحقق ومجموعة الاختبار.

ببساطة، يتم استخدام مجموعة التحقق من الصحة لتحسين معلمات النموذج بينما يتم استخدام مجموعة الاختبار لتوفير تقدير غير متحيز للنموذج النهائي.

يمكن إثبات أن معدل الخطأ كما تم قياسه بواسطة التحقق المتبادل k-fold يميل إلى التقليل من معدل الخطأ الحقيقي بمجرد تطبيق النموذج على مجموعة بيانات غير مرئية.

وبالتالي، فإننا نلائم النموذج النهائي مع مجموعة الاختبار للحصول على تقدير غير متحيز لمعدل الخطأ الحقيقي في العالم الحقيقي.

يوضح المثال التالي الفرق بين مجموعة التحقق من الصحة ومجموعة الاختبار في الممارسة العملية.

مثال: فهم الفرق بين مجموعة التحقق ومجموعة الاختبار

لنفترض أن مستثمرًا عقاريًا يريد استخدام (1) عدد غرف النوم، (2) إجمالي عدد الأقدام المربعة، و(3) عدد الحمامات للتنبؤ بسعر بيع منزل معين.

لنفترض أن لديه مجموعة بيانات تتضمن هذه المعلومات عن 10000 منزل. أولاً، سيتم تقسيم مجموعة البيانات إلى مجموعة تدريب مكونة من 8000 منزل ومجموعة اختبار مكونة من 2000 منزل:

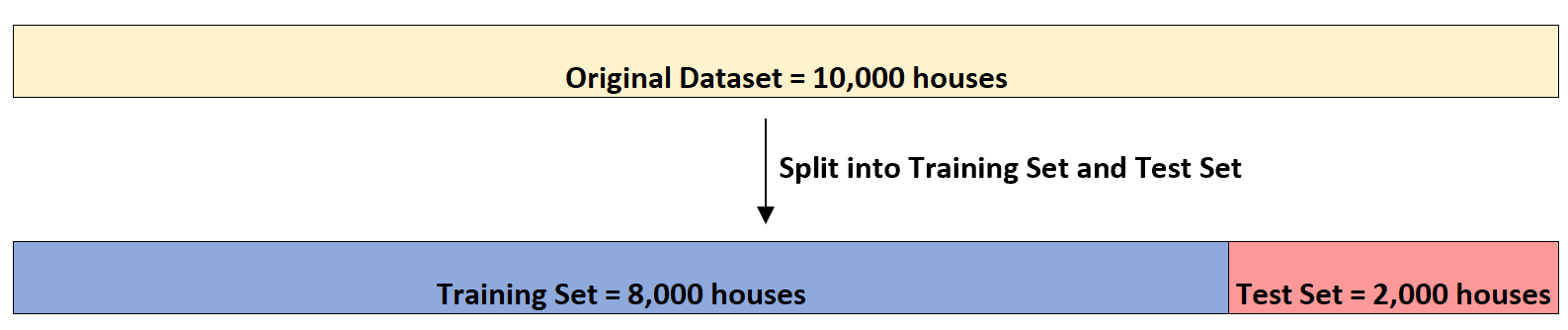
بعد ذلك سوف يتناسب نموذج الانحدار الخطي المتعدد مع مجموعة البيانات أربع مرات. وسوف يستخدم 6000 منزل لمجموعة التدريب و2000 منزل لمجموعة التحقق في كل مرة.

وهذا ما يسمى التحقق المتقاطع k-fold.

يتم استخدام مجموعة التدريب لتدريب النموذج ويتم استخدام مجموعة التحقق لتقييم أداء النموذج. وسوف تستخدم مجموعة مختلفة من 2000 منزل في كل مرة لمجموعة التحقق من الصحة.

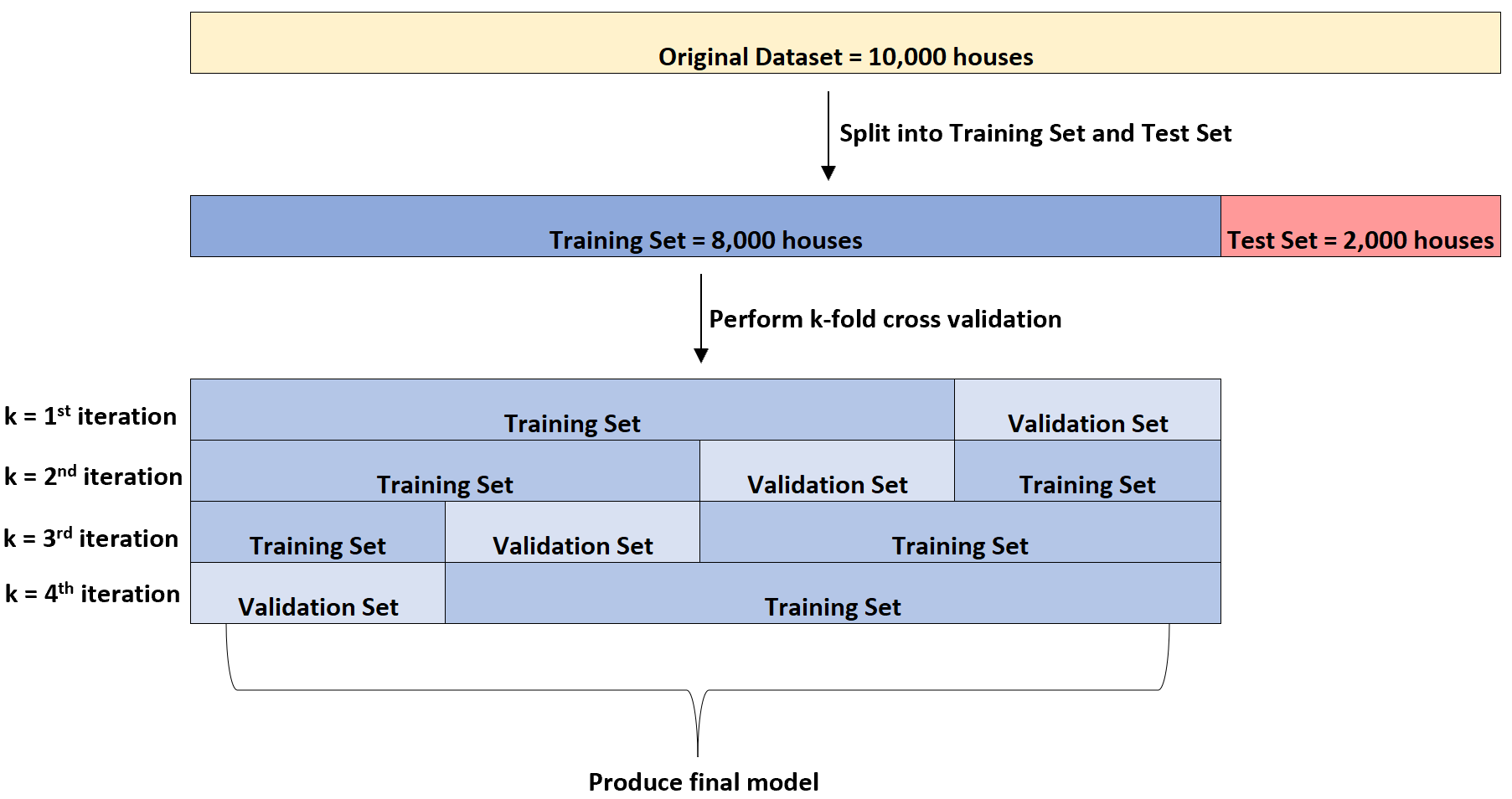
يمكنه إجراء التحقق المتبادل من k-fold على عدة أنواع مختلفة من نماذج الانحدار لتحديد النموذج الذي يحتوي على أقل خطأ (أي تحديد النموذج الذي يناسب مجموعة البيانات بشكل أفضل).

وبمجرد تحديد النموذج الأفضل، سيتم استخدام مجموعة اختبار 2000 منزل التي قدمتها في البداية للحصول على تقدير غير متحيز للأداء النهائي للنموذج.

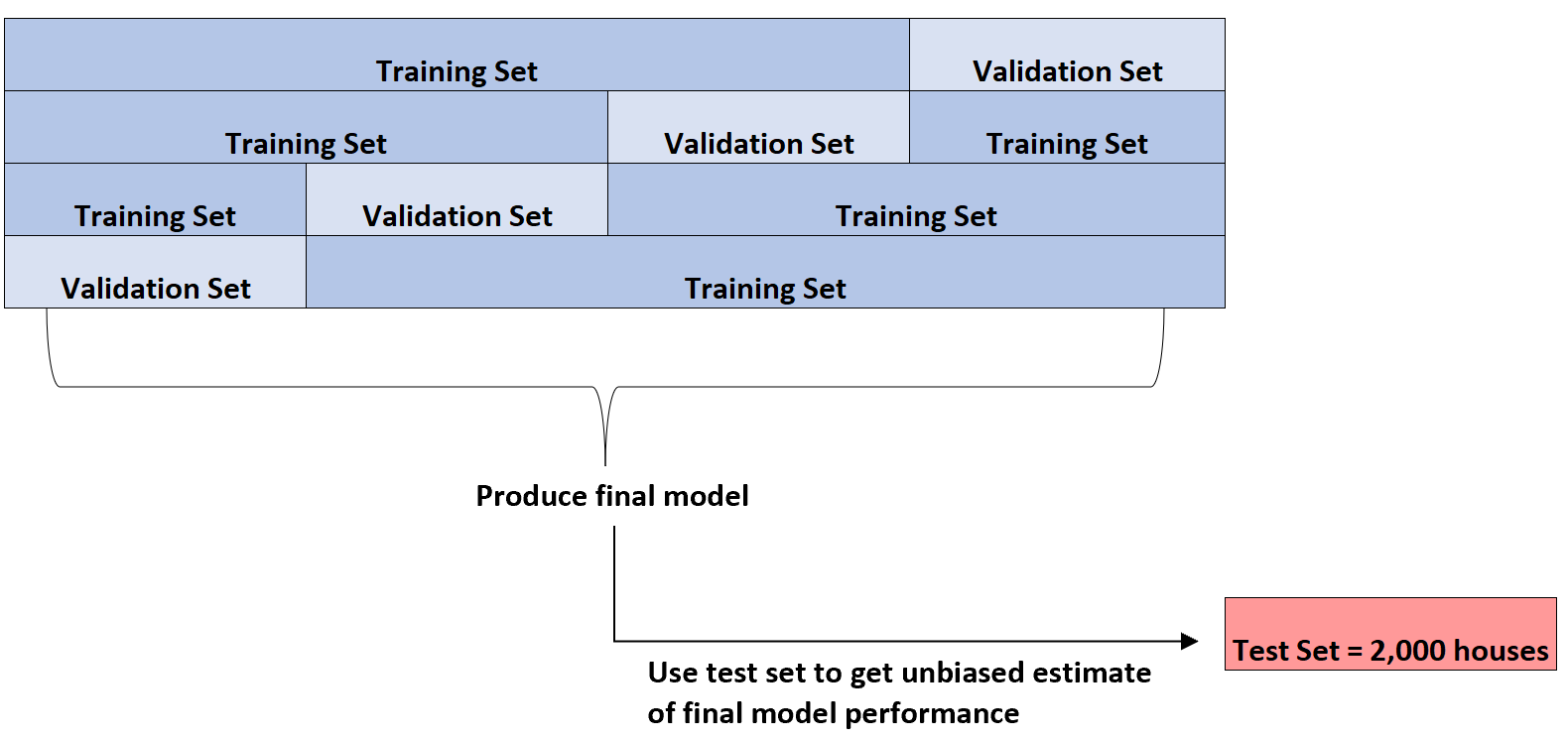
على سبيل المثال، يمكن تحديد نوع معين من نموذج الانحدار الذي يبلغ متوسط خطأه المطلق 8.345 . أي أن متوسط الفرق المطلق بين سعر السكن المتوقع وسعر السكن الفعلي هو 8,345 دولارًا.

ويمكنه بعد ذلك أن يلائم نموذج الانحدار الدقيق هذا مع مجموعة الاختبار المكونة من 2000 منزل لم يتم استخدامها بعد، ويجد أن متوسط الخطأ المطلق للنموذج هو 8.847 .

وبالتالي، فإن التقدير غير المتحيز لمتوسط الخطأ المطلق الحقيقي للنموذج هو 8,847 دولارًا.

مصادر إضافية

دليل بسيط للتحقق من صحة K-Fold
كيفية إجراء التحقق من صحة K-Fold في بايثون
كيفية إجراء التحقق من صحة K-Fold في R