كيفية إجراء anova ثنائي الاتجاه في sas

يتم استخدام ANOVA ثنائي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر تم تخصيصها لمتغيرين (تسمى أحيانًا “العوامل”).

يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية إجراء تحليل التباين ثنائي الاتجاه في SAS.

الخطوة 1: إنشاء البيانات

لنفترض أن عالم النبات يريد معرفة ما إذا كان نمو النبات يتأثر بالتعرض لأشعة الشمس وتكرار الري.

تزرع 30 بذرة وتتركها تنمو لمدة شهر في ظروف مختلفة من التعرض لأشعة الشمس وتكرار الري. وبعد شهر، تسجل ارتفاع كل نبات. النتائج موضحة أدناه:

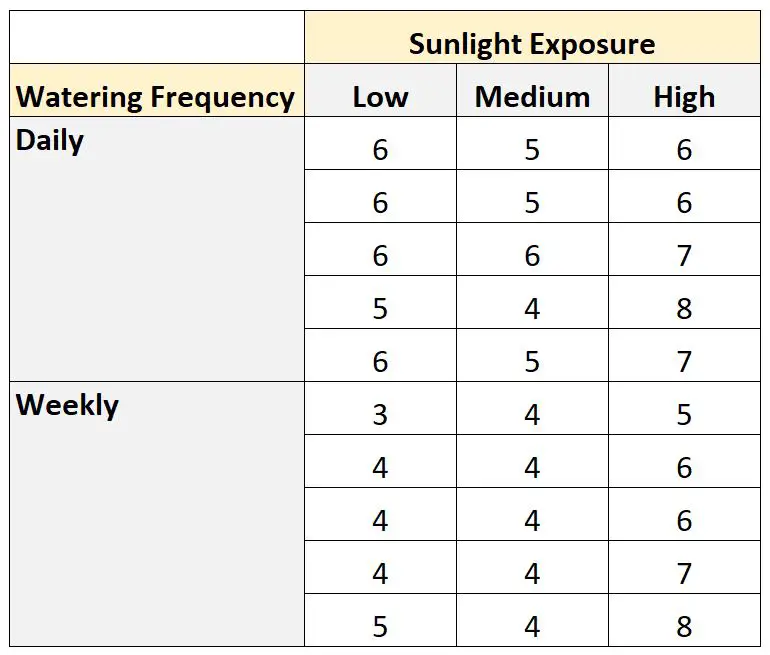
يمكننا استخدام الكود التالي لإنشاء مجموعة البيانات هذه في SAS:

 /*create dataset*/
data my_data;
    input water $sunlight $height;
    datalines ;
daily low 6
daily low 6
daily low 6
daily low 5
daily low 6
daily med 5
daily med 5
daily med 6
daily med 4
daily med 5
daily high 6
daily high 6
daily high 7
daily high 8
daily high 7
weekly low 3
weekly low 4
weekly low 4
weekly low 4
weekly low 5
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly high 5
weekly high 6
weekly high 6
weekly high 7
weekly high 8
;
run ;

الخطوة 2: إجراء تحليل التباين ثنائي الاتجاه

بعد ذلك، سوف نستخدم proc ANOVA لإجراء تحليل التباين ثنائي الاتجاه:

 /*perform two-way ANOVA*/
proc ANOVA data =my_data;
class water sunlight;
model height = water sunlight water*sunlight;
means water sunlight / tukey cldiff ;
run ;

الخطوة 3: تفسير النتائج

الجدول الأول الذي نريد تحليله في النتائج هو جدول ANOVA:

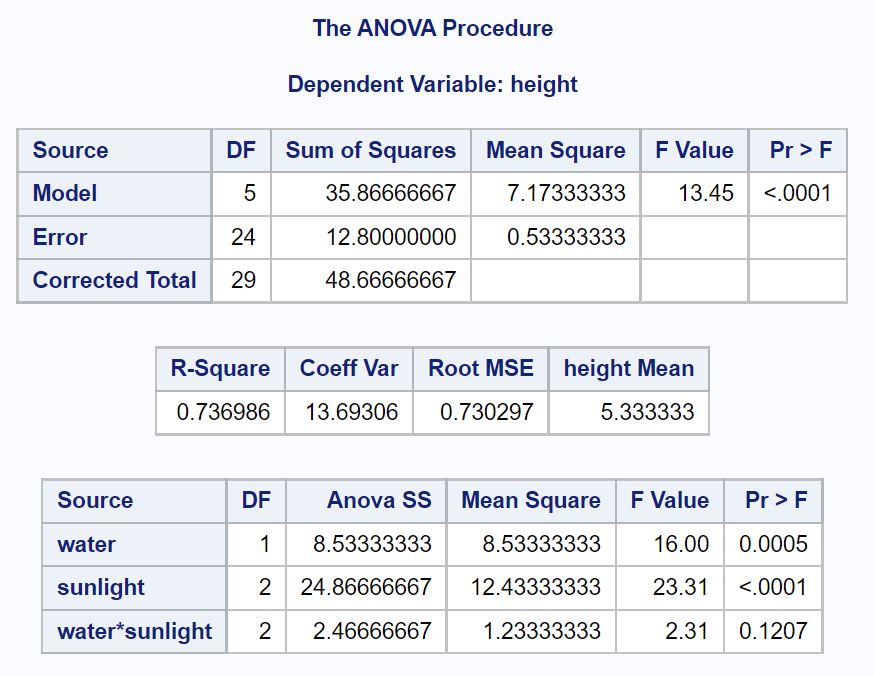
ومن هذا الجدول يمكننا أن نرى:

• القيمة p للمياه: 0.0005
• القيمة p لأشعة الشمس: <.0001
• القيمة p للتفاعل بين الماء وضوء الشمس: . 1207

يخبرنا هذا أن الماء وضوء الشمس يعدان من المؤشرات ذات الأهمية الإحصائية لارتفاع النبات وأنه لا يوجد تأثير تفاعلي ذو دلالة إحصائية بين الماء وأشعة الشمس.

بعد ذلك، يمكننا فحص نتائج اختبارات توكي اللاحقة لتحديد مستويات الماء وضوء الشمس التي تختلف بشكل كبير إحصائيًا.

أولاً، سنلقي نظرة على مقارنات توكي اللاحقة للمياه:

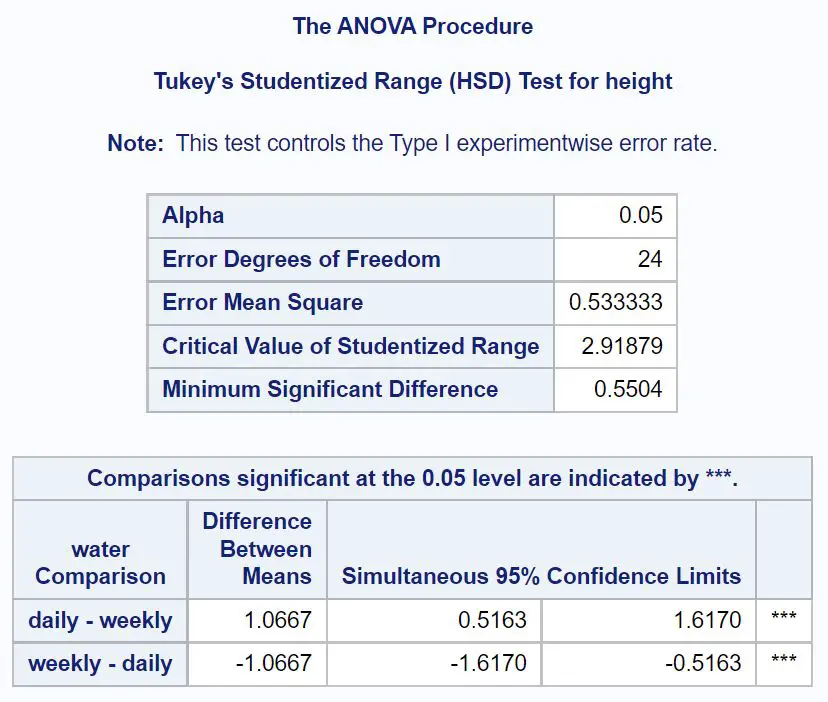
من النتائج يمكننا أن نرى أن متوسط الفرق في الارتفاع بين النباتات التي تسقى يوميا وأسبوعيا كان 1.0667 بوصة.

فاصل الثقة 95% للفرق في متوسط الحجم هو [.5163، 1.6170] . وهذا يعني أننا متأكدون بنسبة 95% من أن الفرق الحقيقي في متوسط الارتفاع بين النباتات التي تسقى يوميًا والنباتات التي تسقى أسبوعيًا يتراوح بين 0.5163 بوصة و1.6170 بوصة.

أولاً، سنلقي نظرة على مقارنات توكي اللاحقة لأشعة الشمس:

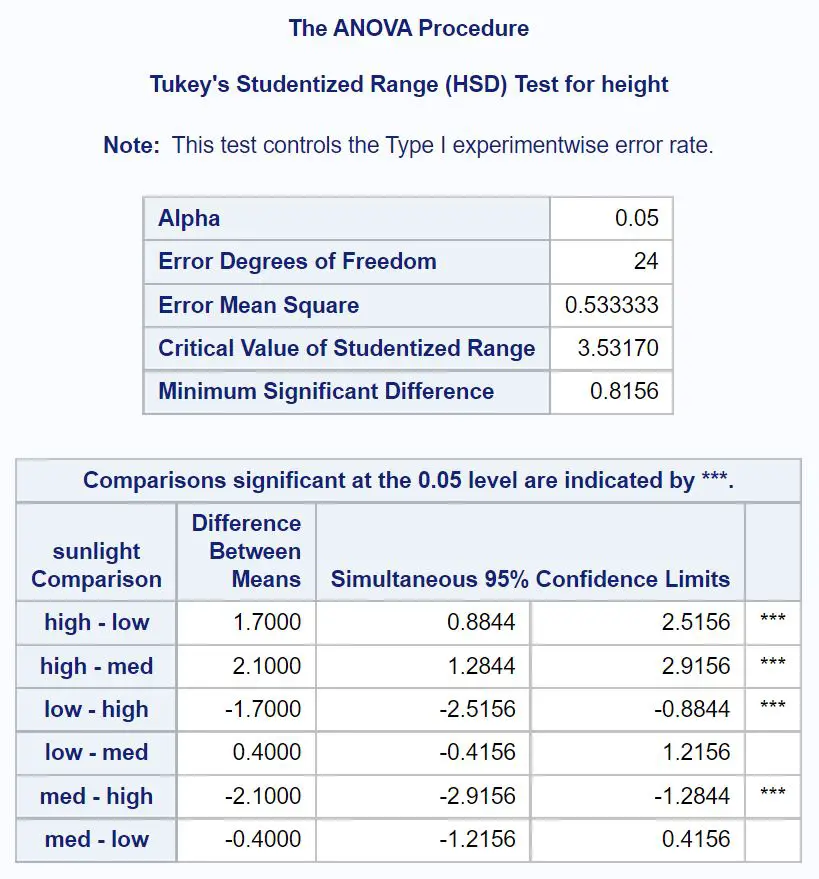
لمعرفة متوسطات المجموعة المختلفة، نحتاج إلى النظر في المقارنات الزوجية التي تحتوي على نجوم ( *** ) بجانبها.

من الجدول يمكننا أن نرى أن متوسطات المجموعات التالية تختلف ذات دلالة إحصائية:

• أشعة الشمس العالية أو أشعة الشمس المنخفضة (95% CI = [.8844، 2.5156])
• أشعة الشمس عالية أو متوسطة (95% CI = [1.2844، 2.9156])

الخطوة 4: تقرير النتائج

وأخيرا يمكننا أن نورد نتائج تحليل التباين الثنائي:

تم إجراء تحليل التباين (ANOVA) ثنائي الاتجاه لتحليل تأثير تكرار الري والتعرض لأشعة الشمس على نمو النبات.

كشفت ANOVA ثنائية الاتجاه أنه لا يوجد تفاعل ذو دلالة إحصائية بين آثار تكرار الري والتعرض للشمس (ع = 0.1207).

أظهر تحليل بسيط للتأثيرات اليدوية أن تكرار الري كان له تأثير ذو دلالة إحصائية على نمو النبات (ع = 0.0005).

أظهر تحليل بسيط لتأثيرات اليد أن التعرض لأشعة الشمس كان له أيضًا تأثير ذو دلالة إحصائية على نمو النبات (P <0.0001).

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول تحليلات التباين (ANOVA) ثنائية الاتجاه:

مقدمة إلى تحليل التباين ثنائي الاتجاه
تحليل التباين أحادي الاتجاه أو ثنائي الاتجاه: متى يتم استخدامه؟
كيفية إجراء تحليل التباين ثنائي الاتجاه يدويًا