مصفوفة التغاير

By دكتور بنيامين أندرسون زومار 5, 2023 إحصائيات 0 Comments

تشرح هذه المقالة ما هي مصفوفة التغاير وما هي صيغتها. سوف تكتشف كيفية إنشاء مصفوفة التغاير باستخدام مثال ملموس وخصائص مصفوفات التغاير.

ما هي مصفوفة التغاير؟

مصفوفة التغاير هي مصفوفة مربعة عناصرها هي تباينات وتباينات المتغيرات المدروسة. وبالتالي، فإن عناصر القطر الرئيسي لمصفوفة التغاير هي تباين كل متغير، والعناصر المتبقية هي التباينات بين المتغيرات.

في الإحصاء، يتم استخدام مصفوفة التغاير لتحليل العلاقة بين متغيرين عشوائيين أو أكثر. تعتبر مصفوفة التغاير مفيدة للغاية لأنها تسمح لك بتفسير الارتباط بين العديد من المتغيرات بسرعة، حيث يمكنك رؤية قيم جميع التغايرات المشتركة للمتغيرات في نفس الوقت.

رمز مصفوفة التغاير هو الحرف اليوناني الكبير سيجما (Σ).

كيفية حساب مصفوفة التغاير

لحساب مصفوفة التباين لعدة متغيرات إحصائية، يجب تنفيذ الخطوات التالية:

حساب الفروق لجميع المتغيرات.
احسب التباين لكل زوج من المتغيرات.
تشكيل مصفوفة التغاير:

يجب وضع تباين المتغير i على القطر الرئيسي للمصفوفة، وبالتحديد في الموضع i,i .
يجب وضع التباين بين المتغيرين i و j في الموضع i,j للمصفوفة.

وبالتالي فإن صيغة مصفوفة التغاير هي كما يلي:

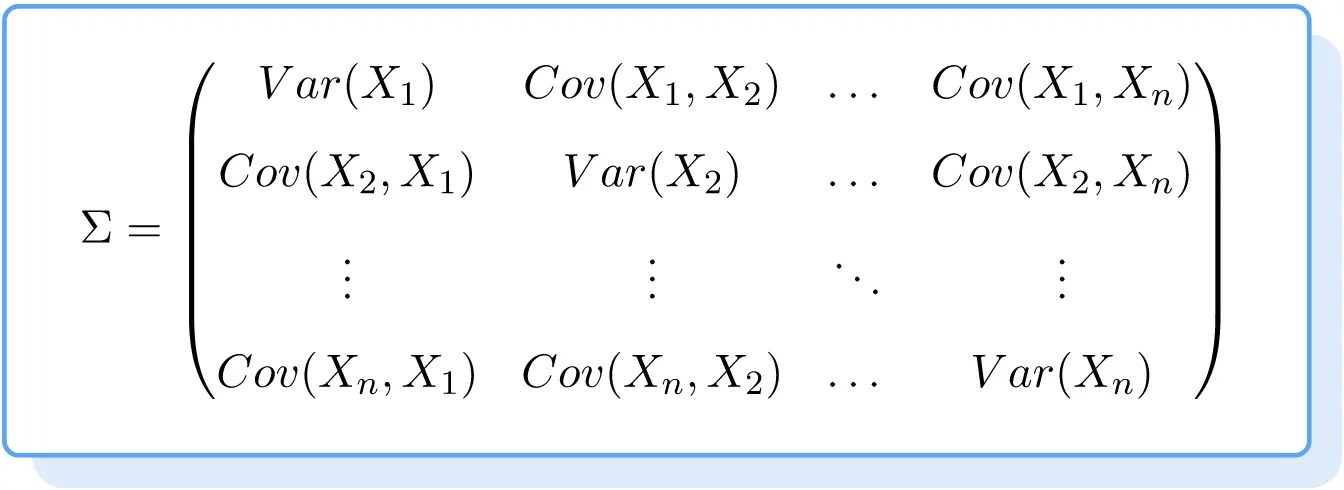
مثال على مصفوفة التغاير

بعد الاطلاع على تعريف مصفوفة التغاير، يوجد أدناه تمرين خطوة بخطوة حتى تتمكن من رؤية كيفية إنشاء هذا النوع من المصفوفات.

يتم حساب مصفوفة التغاير للمتغيرات X وY وZ، والتي تكون قيمها:

العاشر: 4، 7، 12، 5، 7
و: 9، 15، 19، 6، 8
ض: 7، 2، 4، 6، 3

أول شيء يتعين علينا القيام به هو تحديد تباينات جميع المتغيرات:

$Var(X)=7,6$

$Var(Y)=23,44$

$Var(Z)=3,44$

➤ انظر: حاسبة الفجوة

ثانياً، نجد التباين بين كل زوج من المتغيرات:

$Cov(X,Y)=11,2$

$Cov(X,Z)=-2,6$

$Cov(Y,Z)=-4,36$

➤ انظر: حاسبة التغاير

وبمجرد أن نحسب جميع التباينات والتغايرات، كل ما يتبقى هو إنشاء مصفوفة التغاير. للقيام بذلك، نضع قيم التباين على القطر الرئيسي للمصفوفة وقيم التباين في موضعها المقابل:

$\Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}$

$\Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}$

كما ترون، من خلال تمثيل التباينات والتباينات في المصفوفة، فمن السهل جدًا تفسير المتغيرات. المتغير ذو التشتت الأكبر هو Y (23.44)، من ناحية أخرى فإن المتغيرين X و Y لهما علاقة مباشرة، في حين أن المتغيرين X و Z (وبالتالي Y و Z) لهما علاقة عكسية.

لاحظ أن مصفوفة التغاير تكون متماثلة دائمًا، حيث أن التباين بين متغيرين لا يعتمد على ترتيب المتغيرات. على سبيل المثال،

$Cov(X,Y)$

مساوي ل

$Cov(Y,X).$

بالإضافة إلى ذلك، ستكون مصفوفة التغاير دائمًا مصفوفة مربعة وسيكون بعدها مساويًا لعدد المتغيرات. في هذه الحالة كان لدينا ثلاثة متغيرات ولهذا السبب فهي مصفوفة 3×3، لكن إذا كان لدينا متغيرين فقط فإن مصفوفة التغاير ستكون 2×2.

خصائص مصفوفة التغاير

تتميز مصفوفة التغاير بالخصائص التالية:

مصفوفة التغاير هي مصفوفة مربعة مرتبة حسب عدد المتغيرات.
مصفوفة التغاير متماثلة، مما يعني أن القطر الرئيسي للمصفوفة هو محور التماثل.
تكون مصفوفة التغاير دائمًا موجبة وشبه محددة.
محدد مصفوفة التغاير يساوي أو أكبر من الصفر.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر