معامل التحديد (r تربيع)
تشرح هذه المقالة ما هو معامل التحديد (أو مربع R) في الإحصائيات. لذلك، سوف تكتشف كيفية حساب معامل التحديد، وكيفية تفسيره، بالإضافة إلى آلة حاسبة عبر الإنترنت لحساب معامل التحديد لعينة البيانات.
ما هو معامل التحديد (R تربيع)؟
معامل التحديد ، ورمزه R 2 ( R تربيع )، هو إحصائية تقيس مدى ملاءمة نموذج الانحدار. يوضح معامل التحديد مدى ملاءمة نموذج الانحدار لمجموعة بيانات، أي أنه يشير إلى النسبة المئوية التي يوضحها نموذج الانحدار.
ولذلك، كلما ارتفع معامل التحديد، كلما كان نموذج الانحدار أفضل. وعلى الرغم من عدم استيفاء هذا الشرط دائمًا، إلا أننا من حيث المبدأ مهتمون بأكبر قدر ممكن من معامل التحديد. وسنرى أدناه كيفية تفسير معامل التحديد.
صيغة تحديد المعامل
ومعامل التحديد يساوي واحد ناقص النسبة بين التباين المتبقي وتباين المتغير التابع. يمكن أيضًا حساب معامل التحديد عن طريق طرح واحد ناقص مجموع المربعات من البقايا على مجموع المربعات الإجمالي.
وبالتالي، فإن صيغة حساب معامل التحديد هي كما يلي:

ذهب:
-

هو معامل التحديد.
-
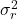
هو التباين المتبقي.
-

هو تباين المتغير التابع Y .
-
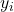
هي قيمة المتغير التابع للملاحظة i.
-
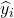
هي القيمة التقريبية بواسطة نموذج الانحدار للمراقبة i.
-

هو متوسط المتغير التابع في جميع الملاحظات.
👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب معامل التحديد لأي مجموعة بيانات.
وفي حالة نموذج الانحدار الخطي فإن معامل التحديد يعادل مربع معامل الارتباط :
![]()
ذهب
![]()
هو التباين المشترك للمتغيرين X و Y،
![]()
و
![]()
هي تباينات المتغير المستقل X والمتغير التابع Y على التوالي.
حاسبة معامل التحديد
قم بإدخال عينة من البيانات في الآلة الحاسبة أدناه لتناسب نموذج الانحدار الخطي البسيط واحسب معامل التحديد الخاص به. تحتاج إلى فصل أزواج البيانات، بحيث يوجد في المربع الأول فقط قيم المتغير المستقل X وفي المربع الثاني يوجد فقط قيم المتغير التابع Y.
يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.
تفسير معامل التحديد
وفي هذا القسم سنرى كيفية تفسير معامل التحديد، لأنه لا فائدة من معرفة قيمة معامل التحديد إذا كنت لا تعرف معناه لاحقاً.
يمكن أن تتراوح قيمة معامل التحديد من 0 إلى 1، ومع ذلك، يتم التعبير عنها عادة كنسبة مئوية، وبالتالي فإن الحد الأدنى هو 0% والحد الأقصى هو 100%.
وفيما يتعلق بتفسير معامل التحديد فكلما زادت قيمته يعني أن نموذج الانحدار يفسر عينة البيانات بشكل أفضل. وبالتالي، كلما اقترب معامل التحديد من 1، كلما زاد تعديل النموذج. ومن ناحية أخرى، كلما اقتربنا من 0، قل موثوقية نموذج الانحدار الناتج.
ومع ذلك، عند مقارنة نموذجين من نماذج الانحدار، فإن النموذج ذو معامل الانحدار الأعلى ليس دائمًا الأفضل. على سبيل المثال، قد يكون لنموذج الانحدار معامل انحدار R 2 = 100% لأنه تمت إضافة العديد من المتغيرات التوضيحية إلى النموذج، وبالتالي يمكنه تفسير جميع الملاحظات بشكل مثالي. ولكن من المؤكد أن هذا النموذج يقدم تنبؤًا سيئًا للغاية لقيمة جديدة لم يتم استخدامها لبناء نموذج الانحدار.
ويجب أيضًا أن يؤخذ في الاعتبار أن نموذج الانحدار الناتج يلبي الافتراضات السابقة. وبالتالي، فإن النموذج ذو معامل التحديد العالي جدًا يكون عديم الفائدة إذا لم يكن تباين بقاياه ثابتًا (التجانس).
علاوة على ذلك، يمثل معامل التحديد حدًا مهمًا، لأنه لا يعاقب على إدراج المتغيرات التفسيرية. منطقيا، كلما زادت المتغيرات التوضيحية لنموذج الانحدار، كلما كان النموذج أكثر تعقيدا، ولكن كلما كان تفسيره للبيانات المرصودة أفضل، وبالتالي، ارتفع معامل التحديد. ومع ذلك، فإن معامل التحديد المعدل يأخذ في الاعتبار عدد المتغيرات في النموذج (سنرى كيف يتم حسابه أدناه).
في الختام، يعتبر معامل التحديد مفيدًا جدًا لتحليل نموذج الانحدار لأنه يتيح لنا معرفة مدى ملاءمة نموذج الانحدار لمجموعة البيانات. ومع ذلك، ينبغي أيضًا استخدام أدوات أخرى لمراجعة النموذج الناتج، مثل الرسوم البيانية الإحصائية .
معامل التحديد المعدل
يقيس معامل التحديد المعدل ، والذي يسمى أيضًا معامل التحديد المعدل ، مدى ملاءمة نموذج الانحدار من خلال مراعاة عدد المتغيرات التوضيحية المدرجة في النموذج.
الفرق بين معامل التحديد ومعامل التحديد المعدل هو أن معامل التحديد يقيس جودة التعديل دون مراعاة عدد المتغيرات، ومن ناحية أخرى فإن معامل التحديد المعدل يقيس جودة التعديل معاقبة لكل متغير مضاف.
صيغة حساب معامل التحديد المعدل هي كما يلي:
![]()
ذهب:
-

هو معامل التحديد المعدل.
-

هو معامل التحديد.
-

هو حجم العينة.
-

هو عدد المتغيرات التوضيحية في نموذج الانحدار.
ولذلك فإن معامل التحديد المعدل أفضل من معامل التحديد للمقارنة بين نموذجين مختلفين، حيث أن النماذج قد تحتوي على عدد مختلف من المتغيرات التوضيحية.