مقارنة درجات z من التوزيعات المختلفة

تخبرك النتيجة z بعدد الانحرافات المعيارية التي تقع قيمة البيانات الفردية عن المتوسط. يتم حسابه على النحو التالي:

النتيجة z = (x – μ) / σ

ذهب:

• x: قيمة البيانات الفردية
• μ: متوسط عدد السكان
• σ : الانحراف المعياري للسكان

يمكن تفسير النتيجة z للقيمة الفردية على النحو التالي:

• درجة Z الإيجابية: القيمة الفردية أعلى من المتوسط.
• درجة z السلبية: القيمة الفردية أقل من المتوسط.
• درجة z تساوي 0: القيمة الفردية تساوي المتوسط.

تكون درجات Z مفيدة بشكل خاص عندما نريد مقارنة الموضع النسبي لنقطتي بيانات من توزيعين مختلفين. لتوضيح ذلك، خذ بعين الاعتبار المثال التالي.

مثال: مقارنة نتائج Z

عادةً ما يتم توزيع الدرجات في اختبار جامعي معين بمتوسط μ = 80 والانحراف المعياري σ = 4. حصل دوان على 84 درجة في هذا الاختبار.

عادةً ما يتم توزيع درجات اختبار جامعي آخر بمتوسط μ = 85 والانحراف المعياري σ = 8. حصلت ديبي على 90 في هذا الاختبار.

مقارنة بتوزيعهم لدرجات الامتحان، من الذي حقق أفضل النتائج في امتحانه؟

للإجابة على هذا السؤال، يمكننا حساب درجة z لدرجة امتحان كل شخص:

درجة دوان z = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

درجة ديبي z = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0.625

على الرغم من أن درجة ديبي أعلى، إلا أن درجة دوان هي في الواقع أعلى مقارنة بتوزيع امتحانه الخاص.

لفهم هذا، فإنه يساعد على تصور الوضع. فيما يلي نتيجة دوان مقارنة بتفاصيل الامتحان الخاص به:

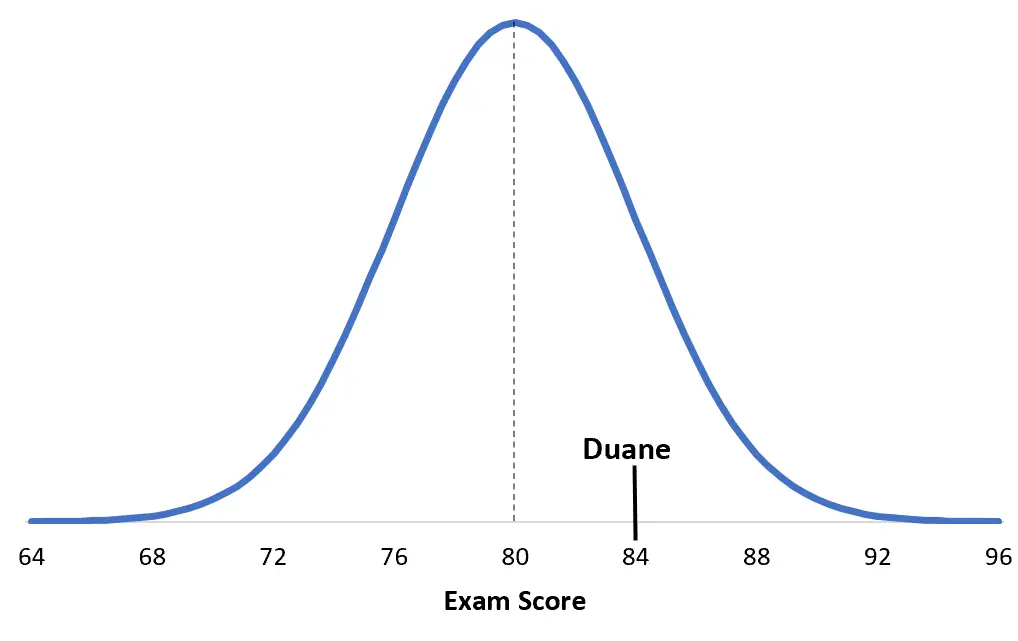
وهذه هي نتيجة ديبي من تفاصيل الامتحان:

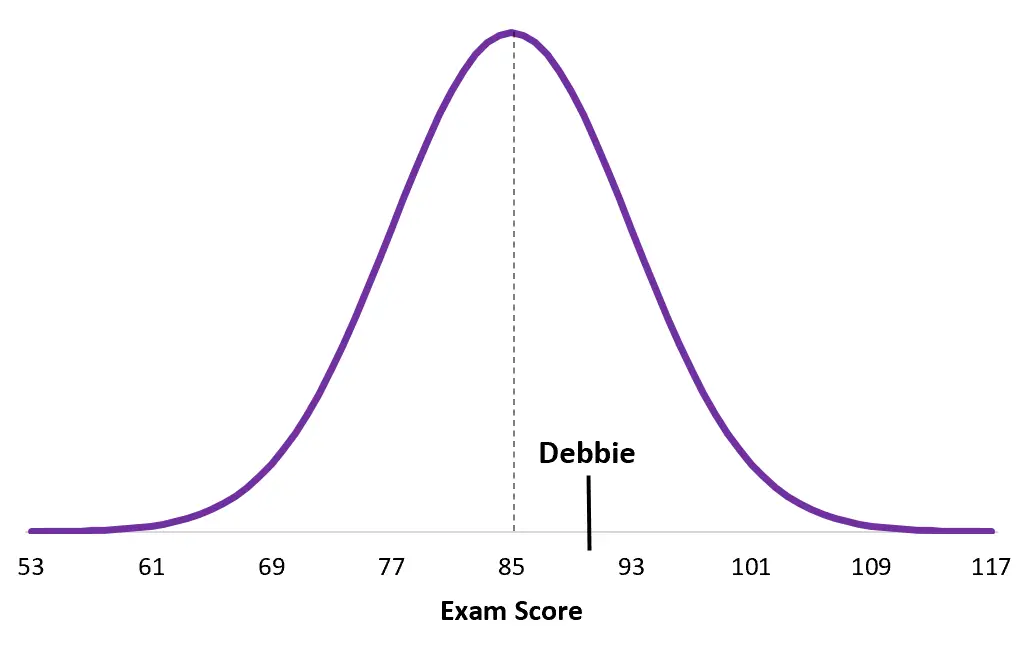
لاحظ مدى قرب درجة ديبي من متوسط عدد سكانها من درجة دوان. على الرغم من أنها حصلت على درجة أعلى بشكل عام، إلا أن درجة Z الخاصة بها أقل ببساطة لأن متوسط الدرجات في امتحانها الخاص أعلى.

يوضح هذا المثال سبب كون درجات z مفيدة جدًا لمقارنة قيم البيانات من توزيعات مختلفة: تأخذ درجات z في الاعتبار المتوسطات والانحرافات المعيارية للتوزيعات، مما يسمح لنا بمقارنة قيم البيانات من توزيعات مختلفة ومعرفة أي منها أعلى مقارنة بتوزيعاتها.

مصادر إضافية

حاسبة النتيجة Z
قارن حاسبة نقاط Z