كيفية إجراء اختبار كولموجوروف-سميرنوف في إكسيل

يتم استخدام اختبار Kolmogorov-Smirnov لتحديد ما إذا كانت العينةموزعة بشكل طبيعي أم لا.

يستخدم هذا الاختبار على نطاق واسع لأن العديد من الاختبارات والإجراءات الإحصائية تفترض أن البيانات يتم توزيعها بشكل طبيعي.

يوضح المثال التالي خطوة بخطوة كيفية إجراء اختبار Kolmogorov-Smirnov على مجموعة بيانات نموذجية في Excel.

الخطوة 1: أدخل البيانات

لنبدأ بإدخال قيم من مجموعة بيانات بحجم عينة n = 20:

الخطوة الثانية: حساب القيم الفعلية والمتوقعة من التوزيع الطبيعي

بعد ذلك سوف نقوم بحساب القيم الفعلية مقابل القيم المتوقعة للتوزيع الطبيعي:

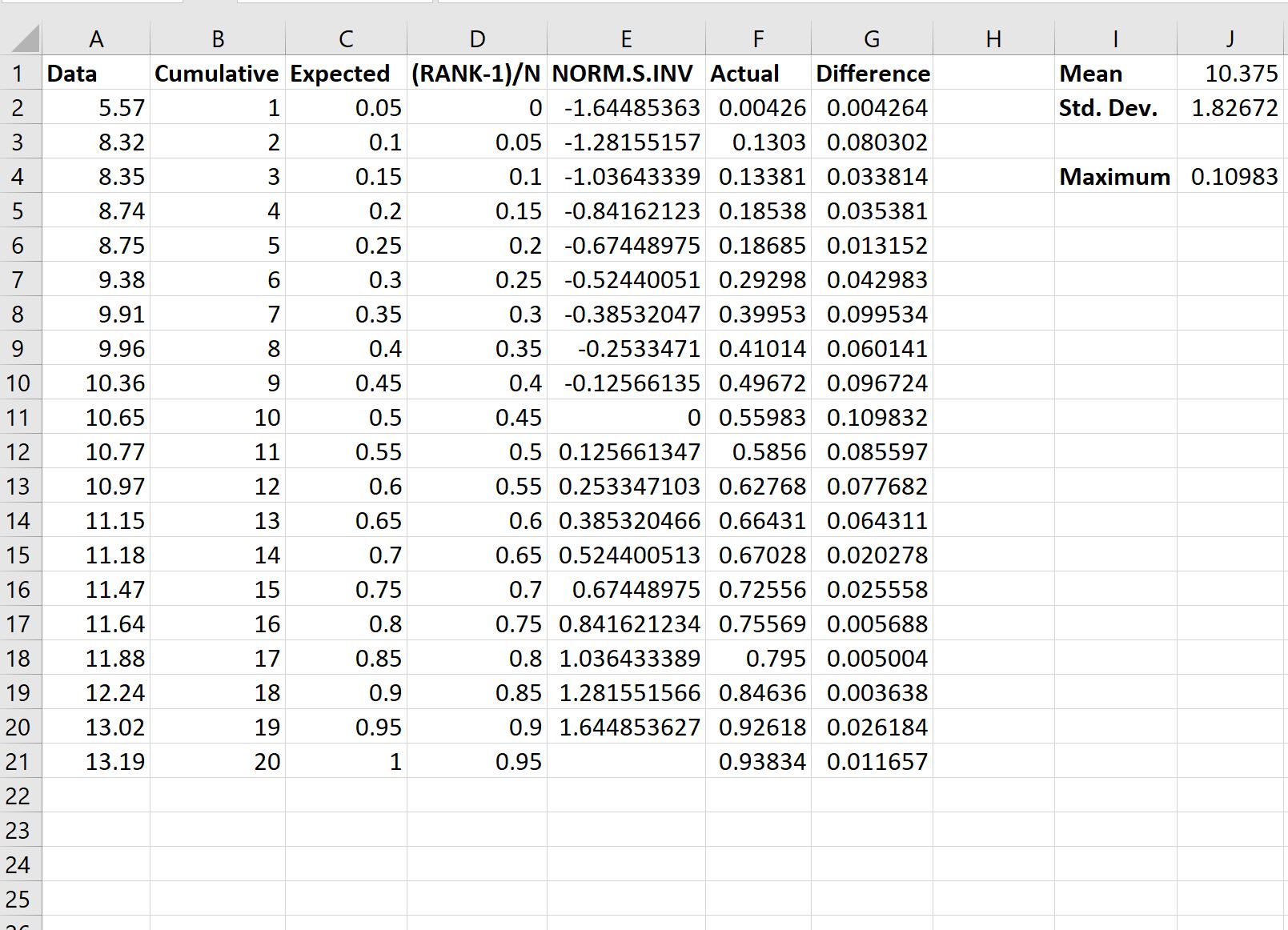
فيما يلي الصيغة التي استخدمناها في خلايا مختلفة:

• B2 : =LINE() – 1
• C2 : = B2 /COUNT( $A$2:$A$21 )
• D2 : =( B2 -1)/COUNT( $A$2:$A$21 )
• E2 : =IF( C2 <1، NORM.S.INV( C2 )،”)
• F2 : =NORM.DIST( A2 , $J$1 , $J$2 , TRUE)
• G2 : =ABS( F2 – D2 )
• D1 : =المتوسط( A2:A21 )
• J2 : =ETDEV.S( A2:A21 )
• J4 : =MAX( G2:G21 )

الخطوة 3: تفسير النتائج

يستخدم اختبار كولموجوروف-سميرنوف الفرضيات الصفرية والبديلة التالية:

• H ₀ : يتم توزيع البيانات بشكل طبيعي.
• HA _A : لا يتم توزيع البيانات بشكل طبيعي.

لتحديد ما إذا كان ينبغي علينا رفض فرضية العدم أم لا، نحتاج إلى الرجوع إلى القيمة القصوى في المخرجات، والتي تبين أنها 0.10983 .

ويمثل هذا الحد الأقصى للفرق المطلق بين القيم الفعلية لعينتنا والقيم المتوقعة للتوزيع الطبيعي.

لتحديد ما إذا كانت هذه القيمة القصوى ذات دلالة إحصائية، يجب الرجوع إلى جدول Kolmogorov-Smirnov للقيم الحرجة والعثور على الرقم الذي يساوي n = 20 و α = 0.05.

وتبين أن القيمة الحرجة هي 0.190 .

وبما أن القيمة القصوى لدينا ليست أكبر من هذه القيمة الحرجة، فإننا نفشل في رفض فرضية العدم.

وهذا يعني أنه يمكننا أن نفترض أن بيانات العينة لدينا يتم توزيعها بشكل طبيعي.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء اختبارات إحصائية شائعة أخرى في Excel:

كيفية إجراء اختبار الارتباط في إكسيل
كيفية إجراء اختبار دوربين-واتسون في برنامج إكسل
كيفية إجراء اختبار جارك بيرا في إكسيل
كيفية إجراء اختبار ليفين في إكسيل