اختبار الطالب
تشرح هذه المقالة ما هو اختبار الطالب وما يتم استخدامه في الإحصاء. وبالتالي، سوف تكتشف كيفية إجراء اختبار الطالب، وما هي الأنواع المختلفة لاختبارات الطالب، وصيغة كل منها.
ما هو اختبار الطالب؟
اختبار t للطالب ، ويسمى أيضًا اختبار T أو ببساطة اختبار t ، هو اختبار إحصائي تتبع فيه إحصائية الاختبار توزيع t للطالب . لذلك، في الإحصاء، يتم استخدام اختبار الطالب لرفض أو قبول الفرضية الصفرية لاختبار الفرضية.
على وجه التحديد، يتم استخدام اختبار الطالب في اختبار الفرضيات الذي يتبع فيه المجتمع قيد الدراسة التوزيع الطبيعي، ولكن حجم العينة صغير جدًا بحيث لا يمكن معرفة تباين المجتمع.
باختصار، يستخدم اختبار الطالب لرفض أو قبول فرضية الدراسة لبعض اختبارات الفرضيات. على سبيل المثال، يتم استخدام اختبار الطالب لاختبار الفرضيات لعينة واحدة، أو لعينات مستقلة، أو لعينات مترابطة. وسنرى بعد ذلك كيف يتم حساب اختبار الطالب في كل حالة.
أنواع اختبارات الطالب
هناك ثلاثة أنواع من اختبارات الطالب :
- اختبار t للطالب لعينة واحدة – يستخدم لاختبار الفرضية حول قيمة متوسط العينة.
- اختبار الطالب لعينتين مستقلتين : يسمح لك باختبار فرضية الفرق بين متوسطي عينتين مستقلتين.
- اختبار الطالب لعينتين مقترنتين (أو العينات ذات الصلة) – يستخدم للتحقيق في الفرضية حول متوسط العينة التي تم اختبارها مرتين.
عينة من اختبار الطالب
اختبارات الفرضية لمتوسط العينة هي تلك التي تقول فيها الفرضية الصفرية والفرضية البديلة للاختبار شيئًا عن قيمة متوسط المجتمع.
صيغة اختبار الطالب t للعينة الواحدة هي كما يلي:

ذهب:
-

هي إحصائية اختبار الفرضية للمتوسط، والتي يتم تحديدها من خلال توزيع الطالب.
-

هي وسيلة العينة.
-

هي قيمة المتوسط المقترح في اختبار الفرضية.
-

هو الانحراف المعياري للعينة.
-

هو حجم العينة.
بمجرد حساب قيمة اختبار الطالب، يجب تفسير نتيجة الاختبار الإحصائي ذات القيمة الحرجة لرفض أو عدم فرضية العدم:
- إذا كان اختبار الفرضية للمتوسط ذو وجهين، فسيتم رفض الفرضية الصفرية إذا كانت القيمة المطلقة لاختبار الطالب أكبر من القيمة الحرجة t α/2|n-1 .
- إذا كان اختبار الفرضية للمتوسط يتطابق مع الذيل الأيمن، فسيتم رفض الفرضية الصفرية إذا كانت قيمة اختبار t للطالب أكبر من القيمة الحرجة t α|n-1 .
- إذا كان اختبار الفرضية للمتوسط يتطابق مع الذيل الأيسر، فسيتم رفض الفرضية الصفرية إذا كانت قيمة اختبار t للطالب أقل من القيمة الحرجة -t α|n-1 .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
لاحظ أنه يتم الحصول على قيم الاختبار الحرجة من جدول توزيع الطالب.
اختبار الطالب للعينات المستقلة
يستخدم اختبار الطالب للعينات المستقلة لرفض أو قبول فرضية وجود علاقة بين متوسطي مجتمعين، على سبيل المثال، أن متوسط مجتمعين مختلفين أو أن متوسط المجتمع A أكبر من متوسط مجتمعين . السكان ب.
ومع ذلك، في هذه الحالة، تختلف صيغة اختبار t للطالب اعتمادًا على ما إذا كان من الممكن افتراض أن تباينات المجتمع متساوية أم لا. وسنرى بعد ذلك الحالتين المحتملتين.
انحرافات غير معروفة ومتساوية
صيغة حساب اختبار الطالب للعينات المستقلة عندما تكون تباينات السكان غير معروفة ولكن من المفترض أن تكون متساوية هي كما يلي:

ذهب:
-

هي إحصائية اختبار الفرضية للفرق بين الوسائل ذات التباينات غير المعروفة، والتي تتبع توزيع الطالب مع n 1 + n 2 -2 درجات الحرية.
-

هو متوسط السكان 1.
-

هو متوسط عدد السكان 2.
-

هو متوسط العينة 1.
-

هو متوسط العينة 2.
-

هو الانحراف المعياري المجمعة.
-

حجم العينة 1.
-

حجم العينة 2.
يتم حساب الانحراف المعياري المشترك للعينتين باستخدام الصيغة التالية:

اختلافات غير معروفة ومختلفة
عندما تكون تباينات السكان غير معروفة، وعلاوة على ذلك، يُفترض أنها مختلفة، تكون صيغة حساب اختبار الطالب للعينات المستقلة كما يلي:

ذهب:
-

هي إحصائية اختبار الفرضية للفرق بين الوسائل ذات التباينات غير المعروفة، والتي تتبع توزيع الطالب.
-

هو متوسط السكان 1.
-

هو متوسط عدد السكان 2.
-

هو متوسط العينة 1.
-

هو متوسط العينة 2.
-

هو الانحراف المعياري للسكان 1.
-

هو الانحراف المعياري للسكان 2.
-

حجم العينة 1.
-

حجم العينة 2.
ومع ذلك، في هذه الحالة، يتم حساب درجات حرية توزيع الطالب باستخدام الصيغة التالية:

اختبار الطالب للعينات المقترنة أو ذات الصلة
يستخدم هذا الاختبار عندما تكون عينتان قيد الدراسة مرتبطتين ببعضهما البعض، بحيث تكون في الواقع عينة واحدة من الأفراد الذين تم تحليلهم مرتين (في كل مرة تحت ظروف مختلفة).
على سبيل المثال، يمكنك تحليل درجات الطلاب في دورة الرياضيات والإحصاء لمعرفة ما إذا كان هناك فرق كبير بين المتوسطات في المادتين. في هذه الحالة، يتم ربط درجة الرياضيات لكل طالب بدرجة الإحصاء الخاصة بالطالب نفسه.
صيغة اختبار الطالب للعينات المقترنة أو ذات الصلة هي:
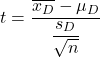
ذهب:
-

هي إحصائية اختبار الفرضية للوسائل المقترنة، والتي يتم تحديدها من خلال توزيع الطالب.
-
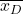
هو متوسط العينة المكونة من اختلاف البيانات.
-
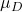
هي قيمة المتوسط المقترح في اختبار الفرضية.
-
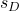
هو الانحراف المعياري للعينة الناتج عن الاختلاف في البيانات.
-

هو حجم العينة.
افتراضات اختبار t للطالب
لإجراء اختبار الطالب، يجب استيفاء الشروط التالية:
- الاستمرارية – بيانات العينة مستمرة.
- العشوائية : تم اختيار عينات البيانات بشكل عشوائي.
- التجانس : أن يكون تباين عينة البيانات متجانساً.
- الحالة الطبيعية – التوزيع الذي يحدد عينة البيانات طبيعي تقريبًا.
كيفية إجراء اختبار الطالب
وأخيرًا، باختصار، تم تفصيل الخطوات التي يجب اتباعها لإجراء اختبار الطالب.
- تحديد الفرضيات الصفرية والبديلة لاختبار الفرضيات.
- تحديد مستوى الأهمية (α) لاختبار الفرضية.
- التحقق من استيفاء افتراضات اختبار الطالب.
- قم بتطبيق صيغة اختبار t للطالب المقابلة واحسب إحصائية الاختبار.
- قم بتفسير نتيجة اختبار الطالب من خلال مقارنتها بالقيمة الحرجة للاختبار.