اختبار الفرضيات للتباين

By دكتور بنيامين أندرسون زومار 3, 2023 إحصائيات 0 Comments

تشرح هذه المقالة ماهية اختبار الفرضيات للتباين. لذا، ستجد صيغة اختبار فرضية التباين، بالإضافة إلى تمرين تم حله خطوة بخطوة.

ما هو اختبار الفرضيات للتباين؟

اختبار فرضية التباين هو طريقة إحصائية تستخدم لتحديد ما إذا كان سيتم رفض الفرضية الصفرية لتباين المجتمع أم لا. بمعنى آخر، يتم استخدام اختبار فرضية التباين لرفض أو قبول الفرضية المتعلقة بقيمة تباين مجتمع ما.

على وجه التحديد، اعتمادًا على قيمة إحصائية اختبار الفرضية للتباين ومستوى الأهمية المختار، يتم رفض الفرضية الصفرية أو قبولها.

ضع في اعتبارك أن اختبار الفرضيات يحمل العديد من الأسماء، وقد يطلق عليه أيضًا اسم تناقضات الفرضيات، أو اختبار الفرضيات، أو اختبار الأهمية.

صيغة اختبار الفرضية للتباين

إن إحصائية اختبار الفرضية للتباين تساوي الفرق بين حجم العينة ناقص مرة واحدة من تباين العينة ومقسمة على القيمة المقترحة لتباين المجتمع. تحتوي إحصائية اختبار الفرضية للتباين على توزيع مربع كاي .

وبالتالي، فإن صيغة حساب إحصائية اختبار الفرضية للتباين هي كما يلي:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

ذهب:

$\chi^2$

هي إحصائية اختبار الفرضية للتباين، والتي لها توزيع مربع كاي.
$n$

هو حجم العينة.
$s^2$

هو تباين العينة.
$\sigma^2$

هو التباين السكاني المقترح.

ولتفسير نتيجة الإحصائية، يجب مقارنة القيمة التي تم الحصول عليها بالقيمة الحرجة للاختبار.

إذا كان اختبار فرضية التباين ثنائي الطرف، فسيتم رفض الفرضية الصفرية إذا كانت الإحصائية أكبر من القيمة الحرجة.
$\chi_{1-\alpha/2|n-1}^2$

أو إذا كانت القيمة الحرجة أقل من

$\chi_{\alpha/2|n-1}$

.
إذا كان اختبار الفرضية للتباين يتطابق مع الذيل الأيمن، فسيتم رفض الفرضية الصفرية إذا كانت الإحصائية أكبر من القيمة الحرجة
$\chi_{1-\alpha|n-1}^2$

.
إذا كان اختبار فرضية التباين يتطابق مع الذيل الأيسر، فسيتم رفض الفرضية الصفرية إذا كانت الإحصائية أقل من القيمة الحرجة
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

يتم الحصول على قيم اختبار الفرضية الحرجة للتباين من جدول توزيع مربع كاي. لاحظ أن درجات الحرية لتوزيع مربع كاي هي حجم العينة ناقص 1.

مثال من العالم الحقيقي لاختبار الفرضيات للتباين

وبعد الاطلاع على تعريف اختبار فرضية التباين وما هي صيغته سنرى مثالا ملموسا للانتهاء من استيعاب المفهوم.

يمتلك أحد المصانع آلة تقوم بإنتاج قطع غيار السيارات بدقة عالية. لكن يشتبه في أنها ابتعدت وأصبحت الآن تصنع أجزاء بفجوة أكبر من 8 ملم ² . لدحض هذه الفرضية، تم تحليل عينة مكونة من 25 قطعة وكان تباين العينة فيها 9.1 ملم ² . هل يمكن رفض الفرضية الأولية بمستوى دلالة α=0.05؟

الفرضية الصفرية والفرضية البديلة لاختبار فرضية التباين هي كما يلي:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”></p> </p> <p style=$ لتحديد ما إذا كان يمكن رفض الفرضية الصفرية أم لا، نقوم بحساب إحصائية اختبار الفرضية للتباين باستخدام الصيغة التي رأيناها أعلاه:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

نحن نبحث الآن عن القيمة الحرجة المقابلة للذيل الأيمن لمدة 24 درجة من الحرية ومستوى الأهمية α=0.05 في جدول توزيع مربع كاي:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

وبذلك تكون الإحصائية المحسوبة أقل من القيمة الحرجة للاختبار وبالتالي لا يتم رفض الفرضية الصفرية لاختبار فرضية التباين، بل يتم رفض الفرضية البديلة.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ انظر: اختبار الفرضيات لمتوسط المجتمع
➤ انظر: اختبار الفرضيات لنسبة السكان

اختبار الفرضية لتباين مجتمعين

يتم استخدام اختبار فرضية التباين بين مجتمعين لرفض أو قبول الفرضية القائلة بأن التباين بين مجتمعين مختلفين متساويان.

وبالتالي فإن الفرضية الصفرية لاختبار الفرضية على التباين بين مجتمعين هي دائمًا ما يلي:

$H_0: \sigma^2_1=\sigma^2_2$

والفرضية البديلة يمكن أن تكون أحد ثلاثة خيارات:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

في هذه الحالة، صيغة حساب إحصائية اختبار الفرضية لتباين مجتمعين هي:

$F=\cfrac{s_1^2}{s_2^2}$

ذهب:

$F$

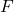
هي إحصائية اختبار الفرضية للتباين بين مجموعتين من السكان، والتي تتبع توزيع F .
$\sigma_1^2$

هو التباين السكاني 1.
$\sigma_2^2$

هو التباين السكاني 2.
$s_1^2$

هو تباين العينة 1.
$s_2^2$

هو تباين العينة 2.
$n_1$

حجم العينة 1.
$n_2$

حجم العينة 2.

نظرًا لأن توزيع Snedecor F غير متماثل، فقد تم رفض فرضية العدم بناءً على المعايير التالية:

[لاتكس]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{أسود} \\text{If}F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر