كيفية إجراء اختبار breusch-pagan في stata

الانحدار الخطي المتعدد هو طريقة يمكننا استخدامها لفهم العلاقة بين المتغيرات التوضيحية المتعددة ومتغير الاستجابة.

لسوء الحظ، هناك مشكلة تحدث غالبًا في الانحدار تُعرف باسم التغايرية ، حيث يوجد تغيير منهجي في تباين القيم المتبقية على نطاق من القيم المقاسة.

أحد الاختبارات التي يمكننا استخدامها لتحديد ما إذا كانت هناك تغايرية هو اختبار بروش باغان . ينتج عن هذا الاختبار إحصائية اختبار مربع كاي وقيمة p المقابلة.

إذا كانت القيمة p أقل من عتبة معينة (الاختيارات الشائعة هي 0.01 و0.05 و0.10)، فهناك أدلة كافية للقول بوجود تغايرية.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار Breusch-Pagan في Stata.

مثال: اختبار Breusch-Pagan في Stata

سوف نستخدم مجموعة بيانات Stata المدمجة تلقائيًا لتوضيح كيفية إجراء اختبار Breusch-Pagan.

الخطوة 1: تحميل وعرض البيانات.

أولاً، استخدم الأمر التالي لتحميل البيانات:

الاستخدام التلقائي للنظام

ثم قم بعرض البيانات الأولية باستخدام الأمر التالي:

ر

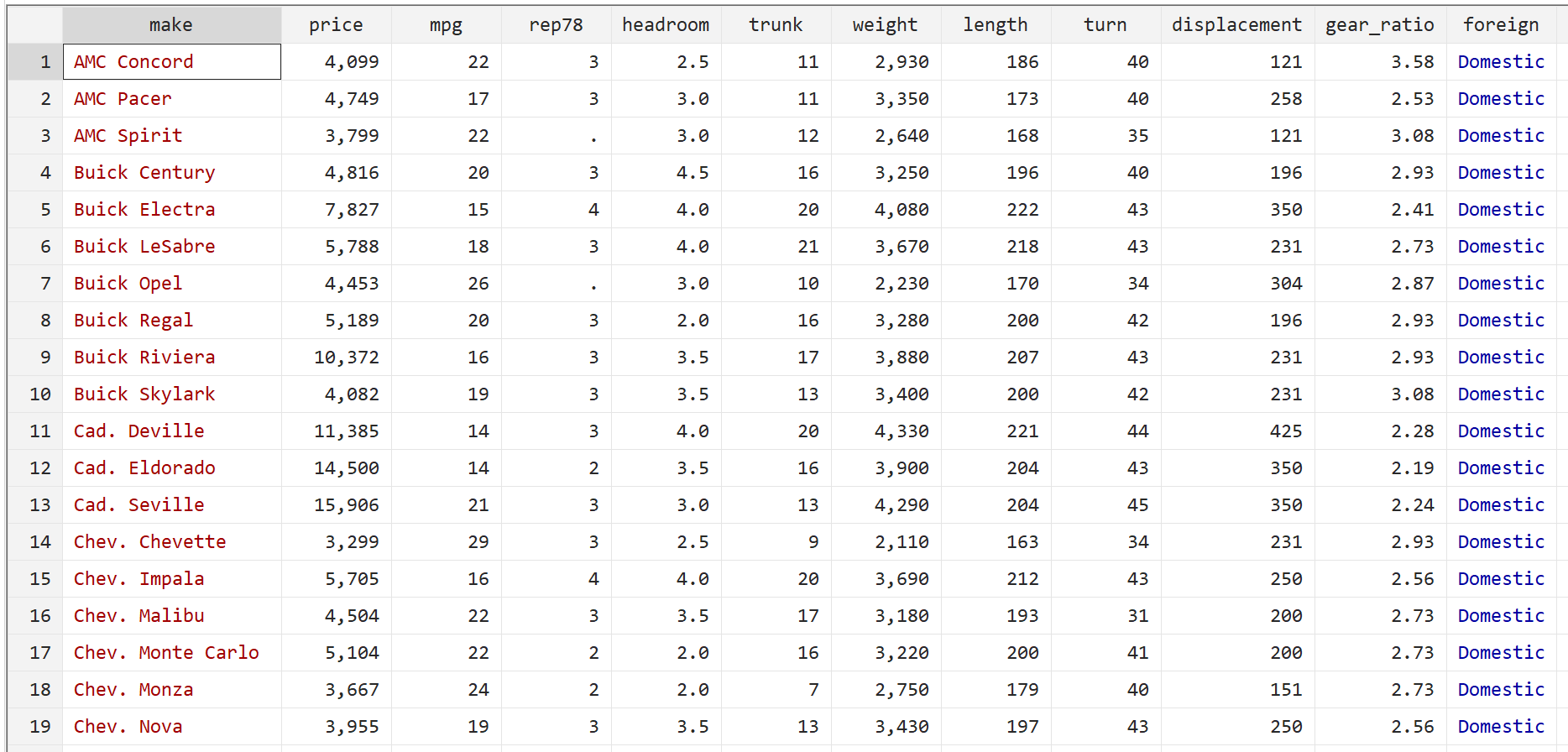
الخطوة 2: تنفيذ الانحدار الخطي المتعدد.

بعد ذلك، سوف نقوم بإدخال الأمر التالي لإجراء انحدار خطي متعدد باستخدام السعر كمتغير الاستجابة والميل لكل غالون والوزن كمتغيرات توضيحية:

سعر الانحدار ميلا في الغالون الوزن

الخطوة 3: إجراء اختبار Breusch-Pagan.

بمجرد الانتهاء من تركيب نموذج الانحدار، يمكننا بعد ذلك إجراء اختبار Breusch-Pagan باستخدام الأمر hetest ، وهو اختصار لـ “heteroscedasticity test”:

الأكثر إثارة

وإليك كيفية تفسير النتيجة:

Ho: هذه هي الفرضية الصفرية للاختبار، والتي تنص على وجود تباين ثابت بين القيم المتبقية.

المتغيرات: يخبرنا بمتغير الاستجابة الذي تم استخدامه في نموذج الانحدار. وفي هذه الحالة كان السعر المتغير.

chi2(1): هذه هي إحصائية اختبار مربع كاي للاختبار. في هذه الحالة، الساعة 2:78 مساءً.

بروب> chi2: هذه هي القيمة p التي تتوافق مع إحصائية اختبار مربع كاي. في هذه الحالة هو 0.0001. وبما أن هذه القيمة أقل من 0.05، فيمكننا رفض فرضية العدم ونستنتج أن هناك تغايرية في البيانات.

ما العمل التالي

إذا فشلت في رفض الفرضية الصفرية لاختبار Breusch-Pagan، فإن التغايرية غير موجودة ويمكنك المتابعة لتفسير نتيجة الانحدار الأصلي.

ومع ذلك، إذا رفضت الفرضية الصفرية لاختبار Breusch-Pagan، فهذا يعني أن التغايرية موجودة في البيانات. في هذه الحالة، تكون الأخطاء القياسية المعروضة في جدول إخراج الانحدار غير موثوقة. هناك عدة طرق لحل هذه المشكلة، بما في ذلك:

1. تحويل متغير الاستجابة. يمكنك محاولة إجراء تحويل على متغير الاستجابة. على سبيل المثال، يمكنك استخدام السجل (السعر) بدلاً من السعر كمتغير الاستجابة. بشكل عام، يعد أخذ سجل متغير الاستجابة طريقة فعالة للتخلص من التغايرية. التحويل الشائع الآخر هو استخدام الجذر التربيعي لمتغير الاستجابة.

2. استخدم الانحدار المرجح. يقوم هذا النوع من الانحدار بتعيين وزن لكل نقطة بيانات بناءً على تباين قيمتها المجهزة. بشكل أساسي، يعطي هذا أوزانًا منخفضة لنقاط البيانات التي تحتوي على تباينات أعلى، مما يقلل من مربعاتها المتبقية. عند استخدام الأوزان المناسبة، يمكن أن يؤدي ذلك إلى القضاء على مشكلة عدم التجانس.

3. استخدم الأخطاء القياسية القوية. تعتبر الأخطاء المعيارية القوية أكثر “قوة” لمشكلة التغايرية وتميل إلى توفير قياس أكثر دقة للخطأ المعياري الحقيقي لمعامل الانحدار. راجع هذا البرنامج التعليمي لمعرفة كيفية استخدام الأخطاء القياسية القوية في الانحدار في Stata.