كيفية إجراء اختبار توكي في r

يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

إذا كانت القيمة الاحتمالية الإجمالية لجدول تحليل التباين (ANOVA) أقل من مستوى معين من الأهمية، فلدينا أدلة كافية لنقول أن إحدى وسائل المجموعة على الأقل تختلف عن الوسائل الأخرى.

ومع ذلك، هذا لا يخبرنا ما هي المجموعات التي تختلف عن بعضها البعض. وهذا يخبرنا ببساطة أنه ليست كل متوسطات المجموعة متساوية. لكي نعرف بالضبط أي المجموعات تختلف عن بعضها البعض، نحتاج إلى إجراء اختبار لاحق .

أحد الاختبارات اللاحقة الأكثر استخدامًا هو اختبار توكي ، والذي يسمح لنا بإجراء مقارنات زوجية بين وسائل كل مجموعة مع التحكم في معدل الخطأ العائلي .

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار Tukey في R.

ملحوظة: إذا كانت أي من المجموعات في دراستك تعتبر مجموعة مراقبة، فيجب عليك استخدام اختبار دونيت كاختبار لاحق بدلاً من ذلك.

مثال: اختبار توكي في R

الخطوة 1: تناسب نموذج ANOVA.

يوضح الكود التالي كيفية إنشاء مجموعة بيانات وهمية بثلاث مجموعات (A وB وC) وملاءمة نموذج ANOVA أحادي الاتجاه مع البيانات لتحديد ما إذا كانت القيم المتوسطة لكل مجموعة متساوية:

 #make this example reproducible
set.seed(0)

#create data
data <- data.frame(group = rep (c("A", "B", "C"), each = 30),
                   values = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#view first six rows of data
head(data)

  group values
1 A 2.6900916
2 A 0.7965260
3 A 1.1163717
4 A 1.7185601
5 A 2.7246234
6 A 0.6050458

#fit one-way ANOVA model
model <- aov (values~group, data=data)

#view the model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)    
group 2 98.93 49.46 30.83 7.55e-11 ***
Residuals 87 139.57 1.60                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

يمكننا أن نرى أن القيمة p الإجمالية من جدول ANOVA هي 7.55e-11 . وبما أن هذا الرقم أقل من 0.05، فلدينا ما يكفي من الأدلة لنقول أن متوسط القيم في كل مجموعة ليس متساويا. لذا، يمكننا إجراء اختبار توكي لتحديد متوسطات المجموعة المختلفة تمامًا.

الخطوة 2: إجراء اختبار توكي.

يوضح التعليمة البرمجية التالية كيفية استخدام وظيفة TukeyHSD() لإجراء اختبار Tukey:

 #perform Tukey's Test
TukeyHSD(model, conf.level= .95 ) 

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = values ~ group, data = data)

$group
         diff lwr upr p adj
BA 0.9777414 0.1979466 1.757536 0.0100545
CA 2.5454024 1.7656076 3.325197 0.0000000
CB 1.5676610 0.7878662 2.347456 0.0000199

تشير القيمة p إلى ما إذا كان هناك فرق ذو دلالة إحصائية بين كل برنامج أم لا. وأظهرت النتائج وجود فرق ذو دلالة إحصائية بين متوسط الوزن المفقود لكل برنامج عند مستوى دلالة 0.05.

خصوصاً:

• قيمة P للفرق في الوسط بين B و A: 0.0100545
• قيمة P للفرق في المتوسطات بين C و A: 0.0000000
• قيمة P للفرق في المتوسطات بين C و B: 0.0000199

الخطوة 3: تصور النتائج.

يمكننا أيضًا استخدام الدالة plot(TukeyHSD()) لتصور فترات الثقة:

 #plot confidence intervals
plot(TukeyHSD(model, conf.level= .95 ), las = 2 )

ملاحظة: تحدد الوسيطة las أن تسميات التجزئة يجب أن تكون متعامدة (las=2) على المحور.

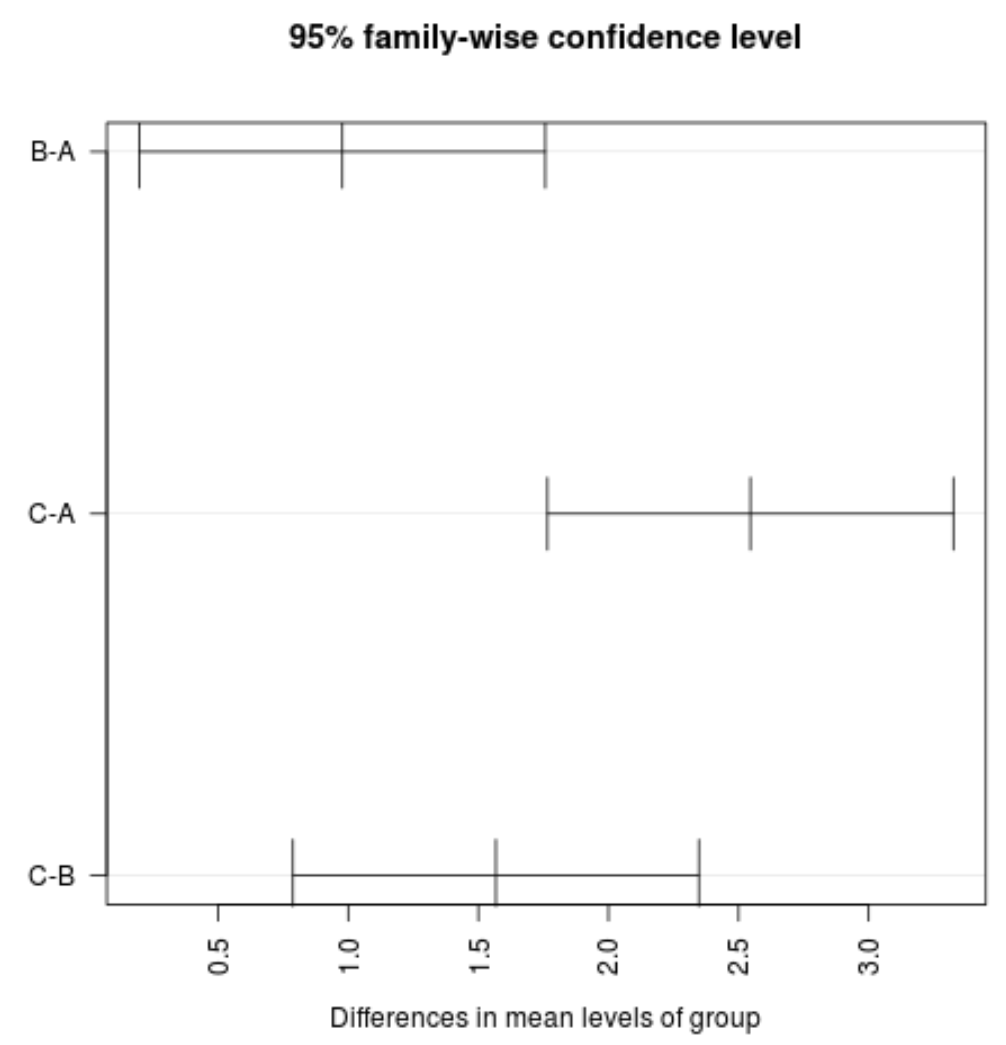
يمكننا أن نرى أن أياً من فترات الثقة لمتوسط القيمة بين المجموعات تحتوي على القيمة صفر، مما يشير إلى وجود فرق ذو دلالة إحصائية في متوسط الخسارة بين المجموعات الثلاث. وهذا يتوافق مع كون جميع القيم p لاختبارات فرضيتنا أقل من 0.05.

ومن هذا المثال بالذات يمكننا أن نستنتج ما يلي:

• القيم المتوسطة للمجموعة C أعلى بكثير من القيم المتوسطة للمجموعتين A و B.
• القيم المتوسطة للمجموعة ب أعلى بكثير من القيم المتوسطة للمجموعة أ.

مصادر إضافية

دليل لاستخدام اختبار ما بعد المخصص مع ANOVA
كيفية إجراء ANOVA أحادي الاتجاه في R
كيفية إجراء ANOVA ثنائي الاتجاه في R