اختبار براون فورسيث في r: مثال خطوة بخطوة
يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق كبير بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.
أحد افتراضات تحليل التباين أحادي الاتجاه هو أن تباينات المجموعات السكانية التي تم سحب العينات منها متساوية.
ومن أكثر الطرق شيوعًا لاختبار ذلك هو استخدام اختبار براون فورسيث ، وهو اختبار إحصائي يستخدمالافتراضات التالية:
- H 0 : الفروق بين السكان متساوية.
- ح أ : الاختلافات بين السكان ليست متساوية.
إذا كانت القيمة p للاختبار أقل من مستوى معين من الأهمية (على سبيل المثال α = 0.05)، فإننا نرفض فرضية العدم ونستنتج أن التباينات ليست متساوية بين المجموعات السكانية المختلفة.
يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية إجراء اختبار Brown-Forsythe في R.
الخطوة 1: أدخل البيانات
لنفترض أننا نرغب في معرفة ما إذا كانت ثلاثة برامج تمرين مختلفة تؤدي إلى مستويات مختلفة من فقدان الوزن أم لا.
ولاختبار ذلك، قمنا بتجنيد 90 شخصًا وتخصيص 30 منهم بشكل عشوائي لاستخدام كل برنامج. ثم نقوم بقياس فقدان الوزن لكل شخص بعد شهر واحد.
تحتوي مجموعة البيانات التالية على معلومات حول مقدار الوزن المفقود مع كل برنامج:
#make this example reproducible set.seed(0) #create data frame data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)), weight_loss = c( runif (30, 0, 3), runif (30, 0, 5), runif (30, 1, 7))) #view first six rows of data frame head(data) # program weight_loss #1 A 2.6900916 #2 A 0.7965260 #3 A 1.1163717 #4 A 1.7185601 #5 A 2.7246234 #6 A 0.6050458
الخطوة الثانية: تلخيص البيانات وتصورها
قبل إجراء اختبار براون فورسيث، يمكننا إنشاء مخططات مربعة لتصور التباين في فقدان الوزن لكل مجموعة:
boxplot(weight_loss ~ program, data = data)
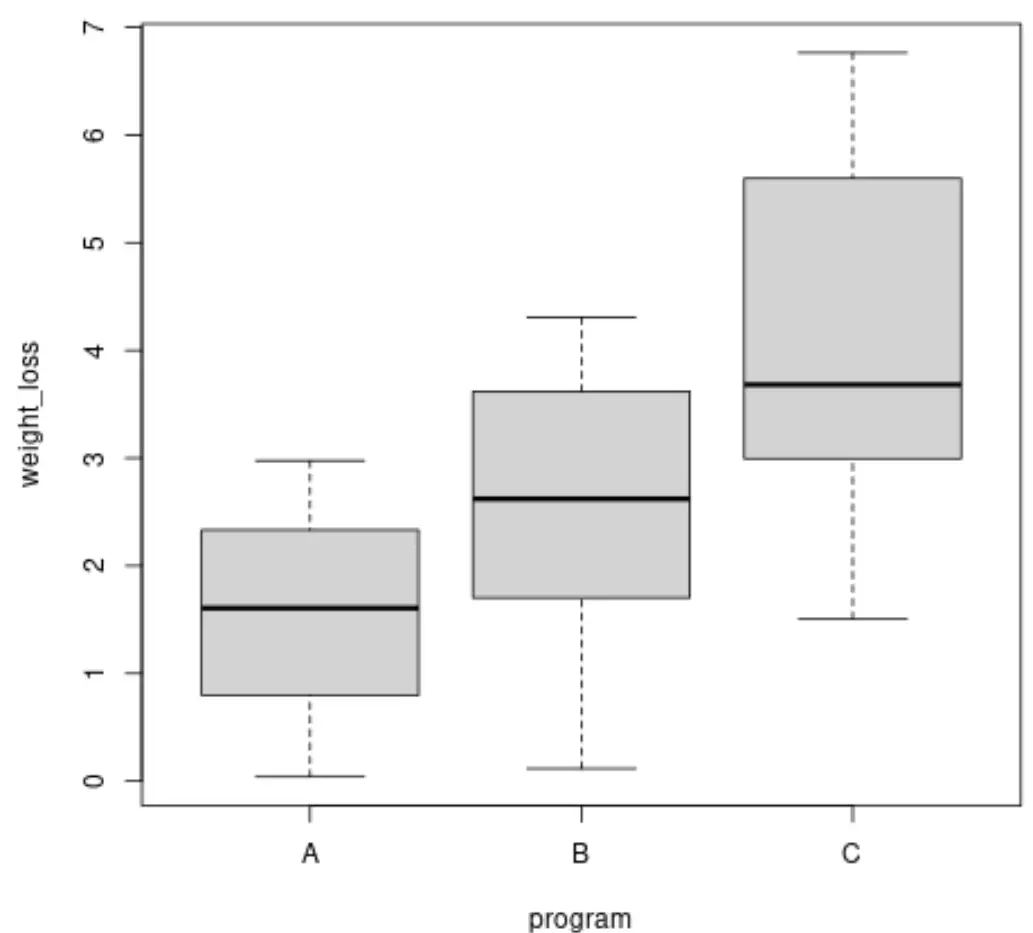
يمكننا أيضًا حساب تباين فقدان الوزن في كل مجموعة:
#load dplyr package library (dplyr) #calculate variance of weight loss by group data %>% group_by (program) %>% summarize (var=var(weight_loss)) # A tibble: 3 x 2 program var 1 A 0.819 2 B 1.53 3 C 2.46
يمكننا أن نرى أن الفروق بين المجموعات تختلف، ولكن لتحديد ما إذا كانت هذه الاختلافات ذات دلالة إحصائية ، يمكننا إجراء اختبار براون فورسيث.
الخطوة 3: إجراء اختبار براون فورسيث
لإجراء اختبار Brown-Forsythe في لغة R، يمكننا استخدام الدالة bf.test() من الحزمة onewaytests :
#load onewaytests package library (onewaytests) #perform Brown-Forsythe test bf.test(weight_loss ~ program, data = data) Brown-Forsythe Test (alpha = 0.05) -------------------------------------------------- ----------- data: weight_loss and program statistic: 30.83304 num df: 2 name df: 74.0272 p.value: 1.816529e-10 Result: Difference is statistically significant. -------------------------------------------------- -----------
وتبين أن القيمة p للاختبار أقل من 0.000، وكما تشير النتيجة، فإن الاختلافات في التباين بين المجموعات الثلاث ذات دلالة إحصائية.
الخطوات التالية
إذا لم تكن قادرًا على رفض الفرضية الصفرية لاختبار براون-فورسيث، فيمكنك إجراء تحليل التباين أحادي الاتجاه على البيانات.
ومع ذلك، إذا رفضت فرضية العدم، فهذا يعني انتهاك افتراض المساواة في التباينات. في هذه الحالة، لديك خياران:
1. قم بإجراء تحليل التباين (ANOVA) في اتجاه واحد على أي حال.
لقد اتضح أن تحليل التباين أحادي الاتجاه يكون في الواقع قويًا بالنسبة للتباينات غير المتساوية طالما أن التباين الأكبر لا يزيد عن 4 أضعاف أصغر التباين.
في الخطوة 2 من المثال أعلاه، وجدنا أن أصغر تباين كان 0.819 وكان أكبر تباين 2.46. وبالتالي فإن نسبة التباين الأكبر إلى الأصغر هي 2.46 / 0.819 = 3.003 .
وبما أن هذه القيمة أقل من 4، فيمكننا ببساطة إجراء تحليل التباين أحادي الاتجاه.
2. إجراء اختبار كروسكال واليس
إذا كانت نسبة التباين الأكبر إلى أصغر التباين أكبر من 4، فيمكن للمرء اختيار إجراء اختبار كروسكال واليس بدلاً من ذلك. ويعتبر هذا المعادل اللامعلمي لتحليل التباين أحادي الاتجاه.
يمكنك العثور على مثال خطوة بخطوة لاختبار Kruskal-Wallis في R هنا .