كيفية إجراء اختبار ليفين في ستاتا

يستخدم اختبار ليفين لتحديد ما إذا كانت مجموعتان أو أكثر لها تباينات متساوية. يستخدم هذا الاختبار على نطاق واسع في الإحصاء لأن العديد من الاختبارات الإحصائية تعتمد على افتراض أن المجموعات لها تباينات متساوية.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار ليفين في ستاتا.

مثال: اختبار ليفين في ستاتا

في هذا المثال، سوف نستخدم مجموعة بيانات الإقامة ، التي تحتوي على معلومات حول مدة إقامة 1,778 مريضًا مختلفًا في المستشفى لإجراء طبي معين، والذي يختلف حسب الجنس. تحتوي مجموعة البيانات على 884 ذكرًا و894 أنثى.

استخدم الخطوات التالية لإجراء اختبار ليفين لتحديد ما إذا كانت الاختلافات في مدة الإقامة متساوية بين الرجال والنساء.

الخطوة 1: تحميل وعرض البيانات.

استخدم الأمر التالي لتحميل مجموعة البيانات في Stata.

استخدم https://www.stata-press.com/data/r13/stay

اعرض الصفوف العشرة الأولى من البيانات باستخدام الأمر التالي:

القائمة في 1/10

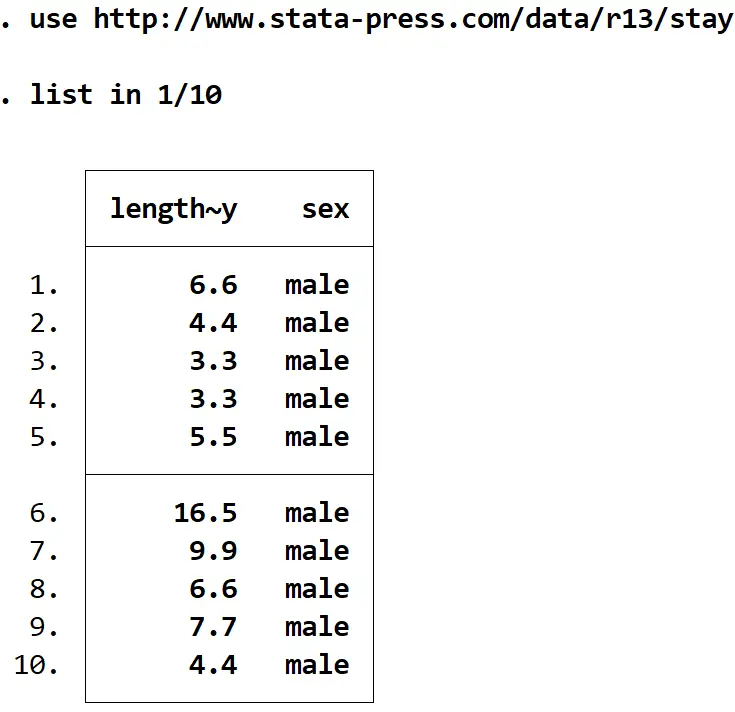
يعرض العمود الأول مدة الإقامة (بالأيام) للفرد ويعرض العمود الثاني جنس الفرد.

الخطوة 2: إجراء اختبار ليفين.

سوف نستخدم بناء الجملة التالي لإجراء اختبار ليفين:

robvar Measure_variable، بواسطة (grouping_variable)

في حالتنا سوف نستخدم بناء الجملة التالي:

مدة إقامة robvar، حسب (الجنس)

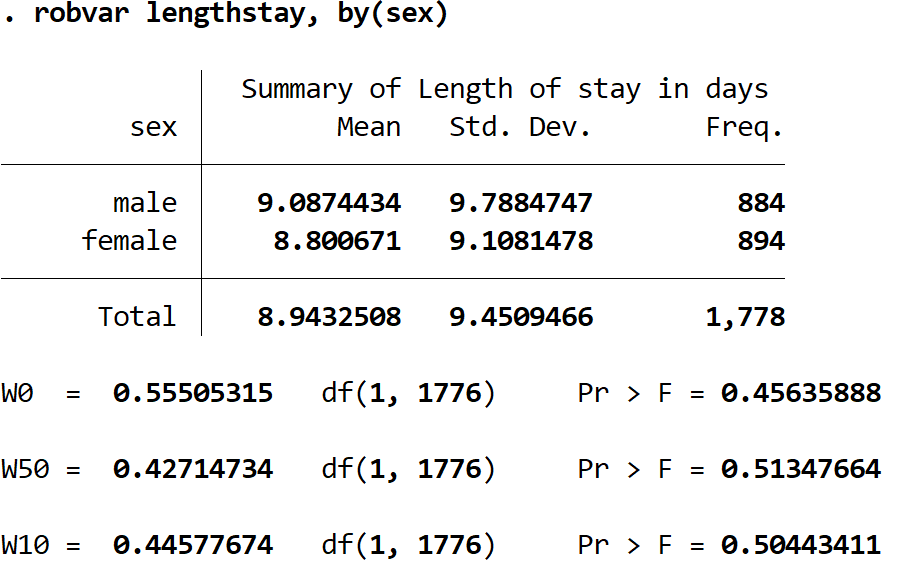
وإليك كيفية تفسير النتيجة:

جدول ملخص: يوضح هذا الجدول متوسط مدة الإقامة، والانحراف المعياري لمدة الإقامة، وإجمالي الملاحظات للرجال والنساء. يمكننا أن نرى أن الانحراف المعياري لمدة الإقامة أعلى عند الرجال (9.7884747) منه عند النساء (9.1081478)، لكن اختبار ليفين سيخبرنا ما إذا كان هذا الفرق ذو دلالة إحصائية أم لا.

W0: 0.55505315 . هذه هي إحصائية اختبار ليفين المتمركزة حول المتوسط. القيمة p المقابلة هي 0.45625888 .

W50: 0.42714734 . هذه هي إحصائية اختبار ليفين المتمركزة حول المتوسط. القيمة p المقابلة هي 0.51347664 .

W10: 0.44577674 . هذه هي إحصائيات اختبار ليفين التي تتمحور حول المتوسط المقطوع بنسبة 10% – أي أنه يتم اقتطاع أعلى 5% وأدنى 5% من القيم حتى لا تؤثر بشكل مفرط على الاختبار. القيمة p المقابلة هي 0.50443411 .

بغض النظر عن إصدار اختبار ليفين الذي تستخدمه، فإن القيمة الاحتمالية لكل إصدار لا تقل عن 0.05. وهذا يدل على عدم وجود فروق ذات دلالة إحصائية في تباين مدة الإقامة بين الرجال والنساء.

ملحوظة: يوصي كونوفر وجونسون وجونسون (1981) باستخدام الاختبار المتوسط للبيانات المنحرفة لأنه يميل إلى تقديم نتائج أكثر دقة. بالنسبة للبيانات المتماثلة، فإن الاختبار المتوسط والاختبار المتوسط سوف يؤديان إلى نتائج مماثلة.