كيفية إجراء اختبار ماكنيمار في ستاتا
اختبار ماكنيمار هو اختبار يمكننا استخدامه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية في النسب بين البيانات المقترنة.
يشرح هذا البرنامج التعليمي كيفية إجراء اختبار McNemar في Stata.
مثال: اختبار ماكنيمار في ستاتا
لنفترض أن الباحثين يريدون معرفة ما إذا كان مقطع فيديو تسويقي معين يمكنه تغيير آراء الأشخاص حول قانون معين. يقومون باستقصاء 100 شخص لمعرفة ما إذا كانوا يدعمون القانون أم لا. ثم يعرضون الفيديو التسويقي لجميع الأشخاص البالغ عددهم 100 شخص ويقومون باستطلاع رأيهم مرة أخرى بعد انتهاء الفيديو.
والجدول التالي يوضح إجمالي عدد الأشخاص الذين أيدوا القانون قبل وبعد مشاهدة الفيديو:
| الفيديو قبل التسويق | ||
|---|---|---|
| الفيديو بعد التسويق | يدعم | لا أستطيع الوقوف |
| يدعم | 30 | 40 |
| لا أستطيع الوقوف | 12 | 18 |
ولتحديد ما إذا كان هناك فرق ذو دلالة إحصائية في نسبة الأشخاص الذين أيدوا القانون قبل وبعد مشاهدة الفيديو، يمكننا إجراء اختبار ماكنمار.
في Stata، يمكننا استخدام الأمر mcci لإجراء اختبار McNemar. نقوم بإدخال الأعداد في الجدول 2×2 من اليسار إلى اليمين، ومن الأعلى إلى الأسفل:
مكي 30 40 12 18
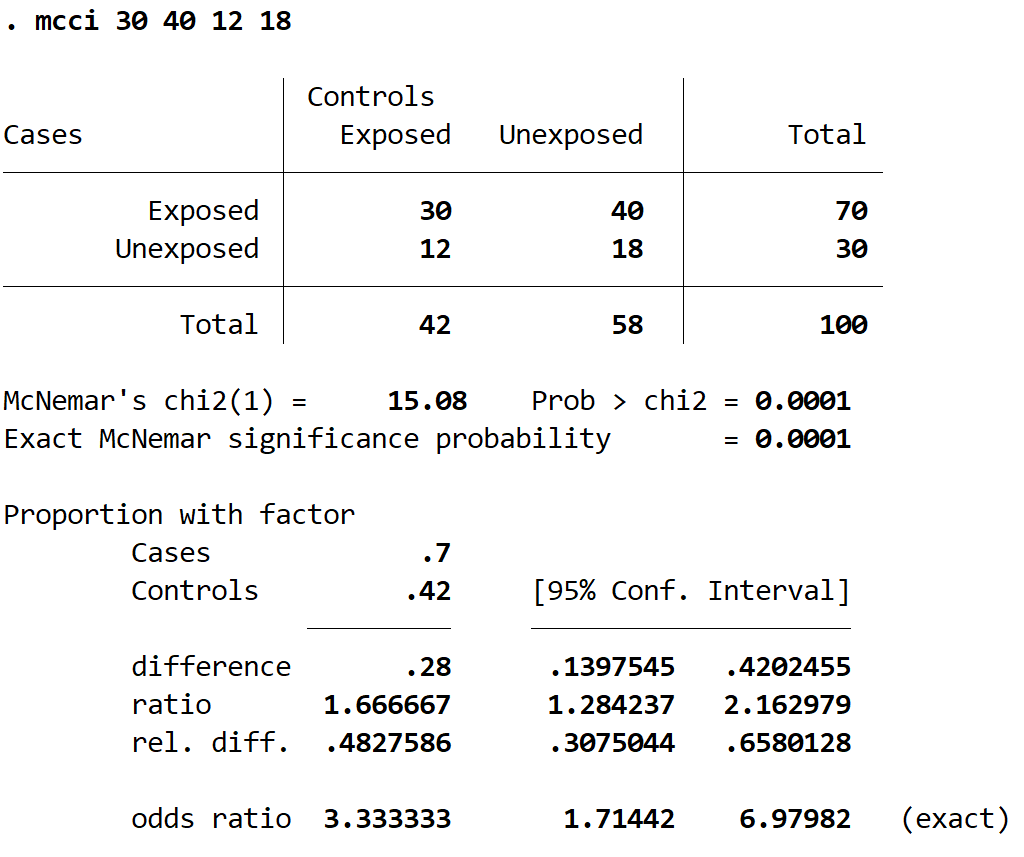
وإليك كيفية تفسير النتيجة:
جدول 2 × 2: تعرض شركة Stata جدول أعداد 2 × 2 باستخدام التسميات التقليدية التي غالبًا ما تظهر في دراسات الحالات والشواهد. يمكننا أن نرى أن إجمالي الحسابات يصل إلى 100.
McNemar’s Chi2(1): هذه هي إحصائية اختبار مربع كاي، والتي تبين أنها 15.08. تستخدم Stata الصيغة التالية لحساب هذه القيمة: (40-12) 2 / (40+12) = 784 / 52 = 15.0769.
بروب> chi2: هذه هي القيمة p المرتبطة بإحصائيات اختبار مربع كاي. وتبين أن 0.0001. وبما أن هذه القيمة أقل من 0.05، يمكننا رفض الفرضية الصفرية ونستنتج أن نسبة الأشخاص الذين أيدوا القانون قبل وبعد مشاهدة الفيديو التسويقي كانت مختلفة ذات دلالة إحصائية.
ملاحظة حول حساب مربع تشي
بالنظر إلى الجدول 2×2 التالي:
| الفيديو قبل التسويق | ||
|---|---|---|
| الفيديو بعد التسويق | يدعم | لا أستطيع الوقوف |
| يدعم | الى | ب |
| لا أستطيع الوقوف | ضد | د |
تستخدم Stata الصيغة (BC) 2 / (B+C) لحساب إحصائية اختبار مربع كاي.
ومع ذلك، تقترح بعض كتب الإحصاء استخدام الصيغة (|BC| – 1) 2 / (B+C) كتصحيح الاستمرارية عندما تكون بعض الأرقام في الجدول صغيرة. عادةً، يتم تطبيق هذا التصحيح عادةً عندما يكون عدد الخلايا أقل من 5.