الاحتمال الشرطي (أو الاحتمال الشرطي)

By زومار 6, 2023 احتمالا 0 Comments

هنا سوف تكتشف ما هو الاحتمال الشرطي (أو الاحتمال الشرطي). نوضح كيفية حساب الاحتمال الشرطي بمثال وخصائص هذا النوع من الاحتمال. بالإضافة إلى ذلك، سوف تكون قادرًا على التدرب على تمارين الاحتمال المشروط التي تم حلها خطوة بخطوة.

ما هو الاحتمال المشروط؟

الاحتمال الشرطي ، ويسمى أيضًا الاحتمال الشرطي ، هو مقياس إحصائي يشير إلى احتمال وقوع الحدث A في حالة وقوع حدث B آخر. أي أن الاحتمال الشرطي P(A|B) يشير إلى احتمال وقوع الحدث A بعد وقوع الحدث B بالفعل.

يُكتب الاحتمال الشرطي بخط عمودي بين الحدثين: P(A|B)، ويُقرأ: “الاحتمال الشرطي للحدث A معين للحدث B”.

لاحظ أن قيمة الاحتمال الشرطي هي رقم يقع بين 0 و1. كلما زاد الاحتمال الشرطي، زاد احتمال وقوع الحدث A عند وقوع الحدث B، ولكن كلما انخفض الاحتمال الشرطي، قل احتمال وقوع الحدث A سيحدث عندما يقع الحدث B.

صيغة الاحتمال الشرطي

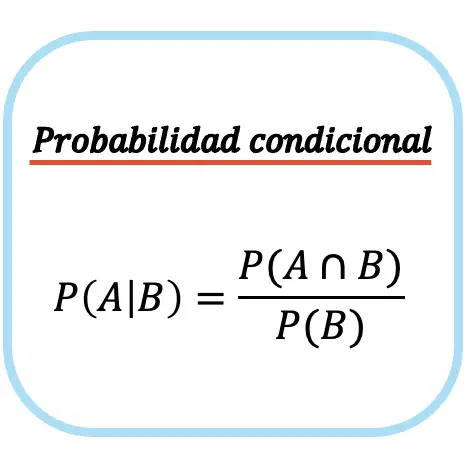
الاحتمال الشرطي للحدث A في ضوء الحدث B يساوي احتمال التقاطع بين الحدث A والحدث B مقسومًا على احتمال الحدث B.

احتمال مشروط أو مشروط

لاحظ أنه لا يمكن استخدام صيغة الاحتمال الشرطي (أو الاحتمال الشرطي) إلا إذا كان احتمال وقوع الحدث غير المشروط غير صفر، أي P(B)≠0. أو بمعنى آخر، إذا كان من الممكن وقوع الحدث B.

يمكن أيضًا حساب الاحتمال الشرطي من معكوسه، أي إذا كانت P(B|A) معروفة، فيمكن تحديد P(A|B). ولكن للقيام بذلك يجب عليك تطبيق نظرية بايز، يمكنك أن ترى مما تتكون هذه النظرية هنا:

➤ انظر: ما هي نظرية بايز؟

مثال على الاحتمال الشرطي

بمجرد أن رأينا ما هو تعريف وصيغة الاحتمال الشرطي، سنحل مثالاً على هذا النوع من الاحتمال خطوة بخطوة لفهم معناه بشكل كامل.

  • بعد إجراء اختبار في فصل مكون من 30 طالبًا، تم جمع البيانات لمعرفة عدد الطلاب الذين درسوا وعدد الطلاب الناجحين. وترد النتائج في جدول الطوارئ التالي. من البيانات المجمعة، احسب الاحتمال الشرطي لاجتياز الاختبار إذا كنت قد درست بالفعل.
حل تمرين الاحتمال الشرطي

للحصول على الاحتمال الشرطي يجب علينا تطبيق الصيغة التي رأيناها سابقاً:

P(\text{aprobado}|\text{estudiado})=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}

لذلك، علينا أولًا إيجاد احتمال أن يكون الطالب قد درس ودرس ونجح. للعثور على احتمال أن يدرس الطالب، نحتاج ببساطة إلى استخدام قاعدة لابلاس، أي أننا نقسم عدد الطلاب الذين درسوا على إجمالي عدد الملاحظات:

P(\text{estudiado})=\cfrac{23}{30}=0,77

ويمكننا معرفة احتمال أن يكون الطالب قد درس وناجح في نفس الوقت من جدول الاحتمالات بقسمة عدد الطلاب الذين درسوا وناجحوا على المجموع:

P(\text{aprobado}\cap \text{estudiado})=\cfrac{19}{30}=0,63

وبالتالي فإن احتمال نجاح الطالب في الامتحان إذا كان قد درس هو:

\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}

الاحتمال الشرطي للأحداث التابعة والمستقلة

في هذا القسم سنرى ما هي العلاقة بين الاحتمال الشرطي والأحداث التابعة والمستقلة (أو الأحداث التابعة والمستقلة). لأنه على الرغم من اختلاف مفهوميهما، إلا أن هذين النوعين من الأحداث مرتبطان باحتمال مشروط.

يكون الحدثان (أو الأحداث) مستقلين عندما لا يعتمد احتمال حدوثهما على بعضهما البعض. وفي مثل هذه الحالة، فإن التقاطع بين الحدثين يعادل حاصل ضرب احتمال كل حدث على حدة. وبالتالي، يتم تبسيط صيغة الاحتمال الشرطي:

P(A|B)=\cfrac{P(A\cap B)}{P(B)}=\cfrac{P(A)\cdot P(B)}{P(B)}=P(A)

باختصار، إذا كان الحدثان A وB مستقلين، فإن الاحتمال الشرطي للحدث A في ضوء الحدث B يساوي تمامًا احتمال وقوع الحدث A.

من ناحية أخرى، عندما يعتمد حدثان، فهذا يعني أن احتمالية حدث واحد تعتمد على احتمالية الحدث الآخر. لذلك، عندما يكون الحدثان A وB معتمدين، فإن الاحتمال الشرطي للحدث A معطيًا للحدث B يختلف عن احتمال وقوع الحدث A.

P(A|B)\neq P(A)

حل تمارين الاحتمال الشرطي

التمرين 1

نحن نعلم أنه في كيس مليء بالكرات، نصفها برتقالي والنصف الآخر أخضر. بالإضافة إلى ذلك، ثلث جميع الكرات برتقالية وفي نفس الوقت تحمل علامة. ما هو احتمال أنه عند رسم كرة برتقالية ستستقبل الإشارة؟

لحل التمرين يجب علينا تطبيق صيغة الاحتمال الشرطية وهي:

P(\text{se\~nal}|\text{naranja})=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}

يخبرنا بيان المشكلة أن نصف الكيس عبارة عن برتقال. ومن ثم، فإن الاحتمال النظري لالتقاط كرة برتقالية هو 50%.

P(\text{naranja})=\cfrac{1}{2}=0,5

ومن ناحية أخرى، نعلم أن ثلث المجموع عبارة عن كرات برتقالية ولها إشارة، وبالتالي فإن احتمال الحصول على كرة برتقالية ذات إشارة هو:

P(\text{se\~nal}\cap \text{naranja})=\cfrac{1}{3}=0,33

أخيرًا، نعوض بالاحتمالات المحسوبة في صيغة الاحتمال الشرطي لإيجاد قيمتها:

\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}

خلاصة الأمر أن احتمال سحب الكرة بالإشارة إذا كانت برتقالية هو 66%.

تمرين 2

إذا كان لدينا ستة أقلام زرقاء وثلاثة أقلام سوداء في صندوق، فاحسب احتمال رسم قلم أزرق واحد واحتمال رسم قلمين أزرقين على التوالي.

لتحديد احتمالية التقاط قلم أزرق مرة واحدة، استخدم قانون لابلاس:

P(\text{azul})=\cfrac{6}{6+3}=0,67

تطلب منا المسألة أيضًا معرفة احتمال التقاط قلمين أزرقين على التوالي، أي الاحتمال الشرطي لالتقاط قلم أزرق إذا كنا قد التقطنا قلمًا أزرق من قبل.

إذا رسمنا بقلم أزرق، فسنحصل على حالة أقل ملاءمة، ولكن هناك أيضًا قلمًا أقل في المجموع. وبالتالي فإن الاحتمال الشرطي هو:

P(\text{azul}|\text{azul})=\cfrac{5}{8}=0,63

التمرين 3

ما الاحتمال المشروط لرمي حجر النرد إلى الرقم 4 إذا كانت رمية العملة المعدنية تؤدي إلى ظهور الصورة؟

لحل هذا التمرين عليك أن تأخذ بعين الاعتبار نظرية الاحتمال المشروط، لأن الحدثين “الحصول على الرقم 4 برمي حجر النرد” و “الحصول على الصورة برمي قطعة نقود” مستقلان. ولذلك ليس من الضروري استخدام صيغة الاحتمال الشرطي، ولكن يتم تحقيق المساواة التالية:

P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})

لذلك، للعثور على الاحتمال الشرطي، ببساطة استخدم قاعدة لابلاس:

P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})=\cfrac{1}{6}=0,167

التمرين 4

تمت دراسة السنة المالية لـ 25 شركة في دولة ما وكيف تتغير أسعار أسهمها حسب النتيجة الاقتصادية لهذا العام. يمكنك الاطلاع على البيانات التي تم جمعها في جدول الطوارئ التالي:

حل تمرين الاحتمال الشرطي

ما مدى احتمالية ارتفاع سعر سهم الشركة إذا حققت ربحًا خلال العام الماضي؟

يسألنا التمرين عن الاحتمال المشروط لارتفاع الأسهم بالنظر إلى أن الشركة قد حققت نتيجة اقتصادية إيجابية. لذا، لحساب هذا الاحتمال، يجب علينا استخدام صيغة الاحتمال الشرطي:

P(\text{precio sube}|\text{beneficio})=\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}

لذلك نحسب أولاً احتمالية تحقيق الشركة ربحًا، وثانيًا، احتمالية تحقيق الشركة ربحًا اقتصاديًا مع زيادة سعر السهم:

P(\text{beneficio})=\cfrac{14}{25}=0,56

P(\text{precio sube}\cap\text{beneficio})=\cfrac{10}{25}=0,4

ثم نستبدل القيم التي تم العثور عليها في الصيغة ونحسب الاحتمال الشرطي:

\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}

خصائص الاحتمال الشرطي

خصائص الاحتمال الشرطي، أو الاحتمال المشروط، هي كما يلي:

  • مجموع الاحتمال الشرطي للحدث A بمعلومية الحدث B بالإضافة إلى الاحتمال المشروط للحدث التكميلي A بمعلومية الحدث B يساوي واحدًا.

P\bigl(A|B\bigr)+P\bigl(\overline{A}|B\bigr)=1

  • إذا كان الحدث A عبارة عن مجموعة فرعية من الحدث B، فسيحدث A دائمًا عندما يكون B صحيحًا. وبالتالي، فإن الاحتمال الشرطي للحدث A معطيًا للحدث B في هذه الحالات هو 1.

B\subseteq A \ \longrightarrow \ P(A|B)=1

  • بالنظر إلى حدثين مختلفين، فإن المساواة التالية فيما يتعلق بالاحتمال الشرطي تكون دائمًا صحيحة:

P\bigl(A\bigr)=P\bigl(A|B\bigr)\cdot P\bigl(B\bigr)+P\bigl(A|\overline{B}\bigl)\cdot P\bigl(\overline{B}\bigr)

About Author

دكتور بنيامين أندرسون
دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر

Add a Comment

ایمئیل یایینلانمایاجاق ایسته‎نیله‎ن بوشلوقلار خاللانمیشدیر *