مقدمة إلى الانحدار الخطي البسيط
الانحدار الخطي البسيط هو أسلوب إحصائي يمكنك استخدامه لفهم العلاقة بين متغيرين، x وy.
يُعرف المتغير x بأنه متغير متوقع .
المتغير الآخر y يعرف بمتغير الاستجابة .
على سبيل المثال، لنفترض أن لدينا مجموعة البيانات التالية بوزن وطول سبعة أفراد:
ليكن الوزن هو المتغير المتنبئ وليكن الارتفاع هو متغير الاستجابة.
إذا رسمنا هذين المتغيرين بيانيًا باستخدام مخطط التشتت، مع الوزن على المحور السيني والارتفاع على المحور الصادي، فهذا هو الشكل الذي سيبدو عليه:
لنفترض أننا نريد أن نفهم العلاقة بين الوزن والطول. من مخطط التشتت يمكننا أن نرى بوضوح أنه مع زيادة الوزن، يميل الطول أيضًا إلى الزيادة، ولكن لتحديد هذه العلاقة بين الوزن والطول، نحتاج إلى استخدام الانحدار الخطي.
باستخدام الانحدار الخطي، يمكننا العثور على الخط الذي “يناسب” بياناتنا بشكل أفضل. يُعرف هذا الخط بخط انحدار المربعات الصغرى ويمكن استخدامه لمساعدتنا في فهم العلاقات بين الوزن والطول.
ستستخدم عادةً برامج مثل Microsoft Excel أو SPSS أو الآلة الحاسبة البيانية للعثور على معادلة هذا الخط.
تتم كتابة صيغة الخط الأفضل:
ŷ = ب 0 + ب 1 س
حيث ŷ هي القيمة المتوقعة لمتغير الاستجابة، وb 0 هو التقاطع، وb 1 هو معامل الانحدار، وx هي قيمة متغير التوقع.
ذات صلة: 4 أمثلة لاستخدام الانحدار الخطي في الحياة الحقيقية
ابحث عن “الخط الأنسب”
في هذا المثال، يمكننا ببساطة إدخال بياناتنا في حاسبة الانحدار الخطي الإحصائي والضغط على “حساب” :
تقوم الآلة الحاسبة تلقائيًا بالعثور على خط انحدار المربعات الصغرى :
ŷ = 32.7830 + 0.2001x
إذا قمنا بتصغير مخطط التشتت السابق وأضفنا هذا الخط إلى الرسم البياني، فهذا هو الشكل الذي سيبدو عليه:
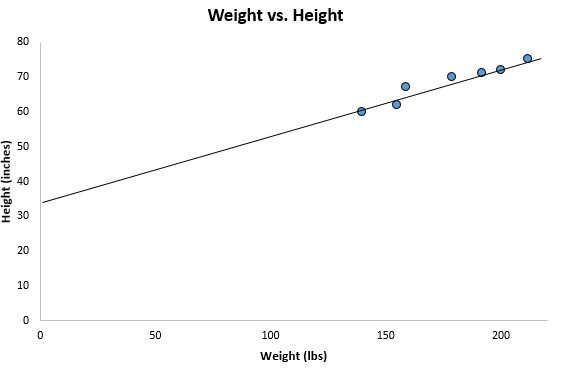
لاحظ كيف أن نقاط البيانات لدينا متناثرة بشكل وثيق حول هذا الخط. وفي الواقع، فإن خط انحدار المربعات الصغرى هذا هو الخط الأكثر ملاءمة لبياناتنا من بين جميع الخطوط المحتملة التي يمكننا رسمها.
كيفية تفسير خط انحدار المربعات الصغرى
فيما يلي كيفية تفسير خط انحدار المربعات الصغرى هذا: ŷ = 32.7830 + 0.2001x
ب0 = 32.7830 . وهذا يعني أنه عندما يكون الوزن المتغير المتنبئ صفر رطل، فإن الارتفاع المتوقع هو 32.7830 بوصة. في بعض الأحيان قد يكون من المفيد معرفة قيمة b 0 ، ولكن في هذا المثال المحدد، ليس من المنطقي تفسير b 0 نظرًا لأن الشخص لا يمكن أن يزن صفر رطل.
ب1 = 0.2001 . هذا يعني أن زيادة وحدة واحدة في x ترتبط بزيادة قدرها 0.2001 وحدة في y . في هذه الحالة، ترتبط الزيادة في الوزن بمقدار رطل واحد بزيادة في الطول بمقدار 0.2001 بوصة.
كيفية استخدام خط انحدار المربعات الصغرى
باستخدام خط انحدار المربعات الصغرى هذا، يمكننا الإجابة على أسئلة مثل:
بالنسبة لشخص يزن 170 رطلاً، ما هو طوله الذي يجب أن نتوقعه؟
للإجابة على هذا السؤال، يمكننا ببساطة إدراج 170 في خط الانحدار الخاص بنا لـ x وحلها لـ y:
ŷ = 32.7830 + 0.2001(170) = 66.8 بوصة
بالنسبة لشخص يزن 150 رطلاً، ما هو طوله الذي يجب أن نتوقعه؟
للإجابة على هذا السؤال، يمكننا إدراج 150 في خط الانحدار الخاص بنا لـ x وحلها لـ y:
ŷ = 32.7830 + 0.2001(150) = 62.798 بوصة
تنبيه: عند استخدام معادلة الانحدار للإجابة على أسئلة مثل هذه، تأكد من استخدام قيم متغير التوقع فقط والتي تقع ضمن نطاق متغير التوقع في مجموعة البيانات. الأصل الذي استخدمناه لإنشاء خط انحدار المربعات الصغرى. على سبيل المثال، تراوحت الأوزان في مجموعة البيانات لدينا بين 140 و212 رطلاً. لذلك فمن المنطقي الإجابة على الأسئلة المتعلقة بالطول المتوقع عندما يتراوح الوزن بين 140 و212 رطلاً.
معامل التحديد
إحدى الطرق لقياس مدى “ملاءمة” خط انحدار المربعات الصغرى للبيانات هي استخدام معامل التحديد ، المشار إليه بـ R 2 .
معامل التحديد هو نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بواسطة المتغير المتنبئ.
يمكن أن يختلف معامل التحديد من 0 إلى 1. وتشير القيمة 0 إلى أن متغير الاستجابة لا يمكن تفسيره بواسطة المتغير المتنبئ على الإطلاق. تشير القيمة 1 إلى أنه يمكن تفسير متغير الاستجابة بشكل مثالي دون أخطاء بواسطة متغير التوقع.
يشير R 2 بين 0 و 1 إلى المدى الذي يمكن من خلاله تفسير متغير الاستجابة بواسطة متغير التوقع. على سبيل المثال، يشير R 2 من 0.2 إلى أن 20% من التباين في متغير الاستجابة يمكن تفسيره بواسطة المتغير المتنبئ؛ تشير قيمة R2 البالغة 0.77 إلى أن 77% من التباين في متغير الاستجابة يمكن تفسيره بواسطة المتغير المتنبئ.
لاحظ أنه في نتيجتنا السابقة حصلنا على R2 بقيمة 0.9311، مما يشير إلى أن 93.11% من التباين في الطول يمكن تفسيره من خلال متغير توقع الوزن:
هذا يخبرنا أن الوزن مؤشر جيد جدًا للطول.
افتراضات الانحدار الخطي
لكي تكون نتائج نموذج الانحدار الخطي صحيحة وموثوقة، يجب علينا التحقق من استيفاء الافتراضات الأربعة التالية:
1. العلاقة الخطية: توجد علاقة خطية بين المتغير المستقل x والمتغير التابع y.
2. الاستقلال: البقايا مستقلة. وعلى وجه الخصوص، لا يوجد ارتباط بين المخلفات المتتالية في بيانات السلاسل الزمنية.
3. المثلية: البقايا لها تباين ثابت عند كل مستوى من x.
4. الحالة الطبيعية: يتم توزيع بقايا النموذج بشكل طبيعي.
إذا لم يتم استيفاء واحد أو أكثر من هذه الافتراضات، فإن نتائج الانحدار الخطي قد تكون غير موثوقة أو حتى مضللة.
ارجع إلى هذه المقالة للحصول على شرح لكل افتراض، وكيفية تحديد ما إذا كان الافتراض قد تحقق، وماذا تفعل إذا لم يتم استيفاء الافتراض.
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر